Введение в математическое программирование - ответы
Количество вопросов - 261

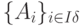 , которому соответствует псевдоплан x, базисные компоненты которого xi = xi0≥0 для всех i є Iδ. При этом
, которому соответствует псевдоплан x, базисные компоненты которого xi = xi0≥0 для всех i є Iδ. При этом 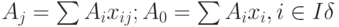 Тогда:
Тогда: определяется уравнением:
определяется уравнением:h1(x1,...,xn) = 0;h2(x1,...,xn) = 0;...............hm(x1,...,xn) = 0.Допустим, что существует такая точка x*, в которой достигается относительный экстремум данной задачи. Если ранг матрицы I = [δhj(x)/δxj], i = 1,...,m; j = 1,...,n в точке x* равен m, то существуют m чисел λ1,...,λn, не все из которых равны нулю одновременно, и при которых:
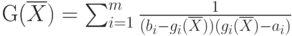 . При этом ограничения в задаче имеют вид:
. При этом ограничения в задаче имеют вид: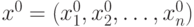 , если для всех точек x, лежащих в малой окрестности точки
, если для всех точек x, лежащих в малой окрестности точки ![[x^0_1, x^0_2 ,\ldots, x^0_n ]](https://intuit.ru//sites/default/files/tex_cache/67a9b05a65fc5309eaf69b117af88149.png) имеет место неравенство:
имеет место неравенство: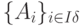 соответствует псевдоплан x. Очевидно, Aj=ΣAixij; A0=ΣAixi, i є Iδ. Известно, что среди базисных компонентов xi имеются отрицательные, причем для некоторого i: xi < 0, а все xij ≥ 0, j=1,...,n. Это значит, что:
соответствует псевдоплан x. Очевидно, Aj=ΣAixij; A0=ΣAixi, i є Iδ. Известно, что среди базисных компонентов xi имеются отрицательные, причем для некоторого i: xi < 0, а все xij ≥ 0, j=1,...,n. Это значит, что: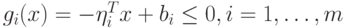 . Для входящего вектора справедливы следующие условия:
. Для входящего вектора справедливы следующие условия:  или
или 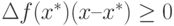 для всех x є S. Тогда множество неотрицательных скаляров {λi} ≥ 0, для которых справедливо соотношение:
для всех x є S. Тогда множество неотрицательных скаляров {λi} ≥ 0, для которых справедливо соотношение: 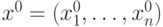 знаки определителей чередуются, т.е. справедливо условие
знаки определителей чередуются, т.е. справедливо условие , то дифференцируемая функция f(x):
, то дифференцируемая функция f(x):a11x1 + a12x2+...+a1nxn ≤ b1 a21x1 + a22x2+...+a2nxn ≤ b2 (1) ......................... am1x1 + am2x2+...+amnxn ≤ bn, x1≥0,x1≥0,...,xn≥0.Тогда множество R(x) является допустимым множеством решений данной задачи, если оно удовлетворяет условиям:
 определяет базисное решение
определяет базисное решение  согласно симплекс – методу, если ограничения задачи линейного программирования имеют вид:
согласно симплекс – методу, если ограничения задачи линейного программирования имеют вид: определяет базисное решение
определяет базисное решение  , которое является допустимым, т.е.
, которое является допустимым, т.е. 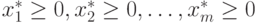 . При этом справедливо равенство: A1x1r+A2x2r+...+Amxmr = Ar. Это значит, что:
. При этом справедливо равенство: A1x1r+A2x2r+...+Amxmr = Ar. Это значит, что: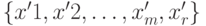 . Связь нового решения
. Связь нового решения 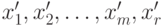 со старым базисным решением
со старым базисным решением  выражается соотношениями
выражается соотношениями  . Тогда уравнение, определяющее старое базисное решение
. Тогда уравнение, определяющее старое базисное решение  , имеет вид:
, имеет вид: , и при этом является допустимым. Выведем одну переменную xi из базисного решения, а соответствующий вектор из базиса. Тогда новое базисное решение имеет вид:
, и при этом является допустимым. Выведем одну переменную xi из базисного решения, а соответствующий вектор из базиса. Тогда новое базисное решение имеет вид: при условиях
при условиях 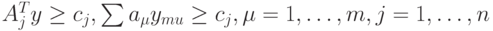 и при этом n ≥ m и ранг матрицы A равен m. Тогда задача, записанная в канонической форме, имеет вид:
и при этом n ≥ m и ранг матрицы A равен m. Тогда задача, записанная в канонической форме, имеет вид: 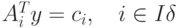 , удовлетворяет ограничениям
, удовлетворяет ограничениям 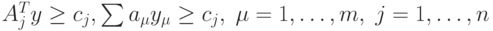 Тогда вектора матрицы ограничений прямой задачи
Тогда вектора матрицы ограничений прямой задачи 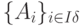 , составляющие сопряженный базис, являются:
, составляющие сопряженный базис, являются: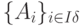 , которому соответствует псевдоплан x. При этом псевдоплан x является оптимальным решением и
, которому соответствует псевдоплан x. При этом псевдоплан x является оптимальным решением и 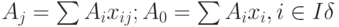 Тогда для базисных компонентов справедливо условие:
Тогда для базисных компонентов справедливо условие: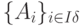 Ему соответствует псевдоплан x. При этом Aj=ΣAixij; A0=ΣAixi, i є Iδ. Известно, что задача неразрешима. Это значит, что базисные компоненты удовлетворяют условиям:
Ему соответствует псевдоплан x. При этом Aj=ΣAixij; A0=ΣAixi, i є Iδ. Известно, что задача неразрешима. Это значит, что базисные компоненты удовлетворяют условиям: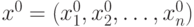 и при этом имеет место равенство
и при этом имеет место равенство  . Это справедливо:
. Это справедливо: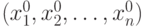 области R функция достигает относительного максимума, то:
области R функция достигает относительного максимума, то: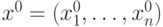 , если выполняются следующие условия:
, если выполняются следующие условия:h1(x1,...,xn) = 0;h2(x1,...,xn) = 0;...............hm(x1,...,xn) = 0.Пусть в некоторой точке x* ранг матрицы I = [δhj(x)/δxj], i = 1,...,m; j = 1,...,nравен m, и существуют m чисел λ1,...,λn, не все из которых равны нулю одновременно, и при которых Δf(x*) + ΣλiΔhi(x) = 0, i = 1,...,m. Тогда в точке x*:
 определяет базисное решение
определяет базисное решение  . Новое решение
. Новое решение 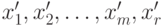 связано со старым базисным решением
связано со старым базисным решением  соотношениями:
соотношениями:  Тогда уравнение имеет вид:
Тогда уравнение имеет вид: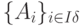 , базисное решение y соответствующей системы линейных уравнений вида
, базисное решение y соответствующей системы линейных уравнений вида 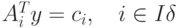 , удовлетворяет ограничениям
, удовлетворяет ограничениям 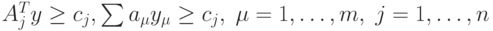 Тогда данная система носит название:
Тогда данная система носит название: . Тогда согласно метода Кэррола присоединенная функция имеет вид:
. Тогда согласно метода Кэррола присоединенная функция имеет вид: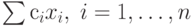 , то условия имеют вид:
, то условия имеют вид: определяет базисное решение
определяет базисное решение  . Предположим, что это решение допустимо, т.е.
. Предположим, что это решение допустимо, т.е. 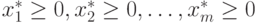 . Если Аr не входит в базис, то:
. Если Аr не входит в базис, то: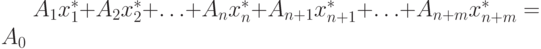 определяет базисное решение
определяет базисное решение  .Новое решение
.Новое решение 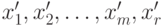 базисное решение связано со старым базисным решением
базисное решение связано со старым базисным решением  соотношениями:
соотношениями:  . Данное решение будет допустимым, если:
. Данное решение будет допустимым, если:  , и при этом выполняется соотношение
, и при этом выполняется соотношение  , т.е. данное решение является допустимым. Чтобы данное решение являлось базисным, необходимо:
, т.е. данное решение является допустимым. Чтобы данное решение являлось базисным, необходимо: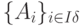 , для которой базисное решение y соответствующей системы линейных уравнений вида
, для которой базисное решение y соответствующей системы линейных уравнений вида 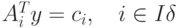 , удовлетворяет ограничениям:
, удовлетворяет ограничениям: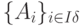 соответствует псевдоплан x. Среди базисных компонентов xi имеются отрицательные, причем для некоторого i: xi < 0, а все xij ≥ 0, j=1,...,n. Это значит, что задача неразрешима. Следовательно, справедливы соотношения:
соответствует псевдоплан x. Среди базисных компонентов xi имеются отрицательные, причем для некоторого i: xi < 0, а все xij ≥ 0, j=1,...,n. Это значит, что задача неразрешима. Следовательно, справедливы соотношения: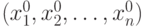 допустимой области R функция достигает относительного максимума и при этом справедливо равенство ∂f(x0)/∂xj = 0, j=1,...,n, то:
допустимой области R функция достигает относительного максимума и при этом справедливо равенство ∂f(x0)/∂xj = 0, j=1,...,n, то: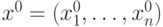 знаки определителей чередуются, т.е. справедливо условие
знаки определителей чередуются, т.е. справедливо условие , то функция f(x):
, то функция f(x): h1(x1,...,xn) = 0;h2(x1,...,xn) = 0;...............hm(x1,...,xn) = 0.Допустим, что существует такая точка x*, в которой достигается относительный экстремум данной задачи.Известно, что существуют m чисел λ1,...,λn, не все из которых равны нулю одновременно, и при которых Δf(x*) + ΣλiΔhi(x) = 0, i = 1,...,m. Тогда:
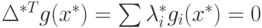 . Тогда вектор Δ*:
. Тогда вектор Δ*: 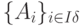 , которому соответствует псевдоплан x. Базисные компоненты псевдоплана удовлетворяют условиям xi = xi0≥0 для всех i є Iδ. При этом псевдоплан x является оптимальным решением. Тогда справедливы соотношения:
, которому соответствует псевдоплан x. Базисные компоненты псевдоплана удовлетворяют условиям xi = xi0≥0 для всех i є Iδ. При этом псевдоплан x является оптимальным решением. Тогда справедливы соотношения: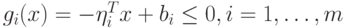 . Для входящего вектора справедливы следующие условия:
. Для входящего вектора справедливы следующие условия:  или
или 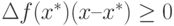 для всех x є S.Тогда скаляры {λi}, для которых справедливо соотношение Δf(x*)=Σλiηi(x) = -ΣλiΔgi(x*), i є I, являются:
для всех x є S.Тогда скаляры {λi}, для которых справедливо соотношение Δf(x*)=Σλiηi(x) = -ΣλiΔgi(x*), i є I, являются:a11x1 + a12x2+...+a1nxn ≤ b1 a21x1 + a22x2+...+a2nxn ≤ b2 (1) ......................... am1x1 + am2x2+...+amnxn ≤ bn, x1≥0,x1≥0,...,xn≥0.Тогда допустимым множеством решений задачи называется:
 определяет базисное решение
определяет базисное решение  . При этом Ar не входит в базис, т.е. справедливо равенство: A1x1r+A2x2r+...+Amxmr = Ar. Тогда базисное решение имеет вид:
. При этом Ar не входит в базис, т.е. справедливо равенство: A1x1r+A2x2r+...+Amxmr = Ar. Тогда базисное решение имеет вид: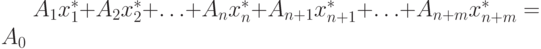 определяет базисное решение
определяет базисное решение  . Обозначим решение уравнения A1x1+A2x2+...+Amxm+Arxr = А0 как
. Обозначим решение уравнения A1x1+A2x2+...+Amxm+Arxr = А0 как 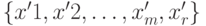 . Тогда связь нового решения
. Тогда связь нового решения 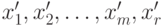 со старым базисным решением
со старым базисным решением  выражается следующими соотношениями:
выражается следующими соотношениями: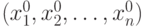 области R функция:
области R функция: при условиях
при условиях 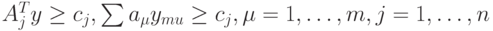 Тогда выполняется условие:
Тогда выполняется условие:a11x1 + a12x2+...+a1nxn ≤ b1 a21x1 + a22x2+...+a2nxn ≤ b2 ......................... am1x1 + am2x2+...+amnxn ≤ bn, x1≥0,x1≥0,...,xn≥0,является:
 . При этом имеет место соотношение:
. При этом имеет место соотношение:  . Тогда новое решение:
. Тогда новое решение:  . Тогда условия ограничения имеют вид:
. Тогда условия ограничения имеют вид:  , и при этом выполняется соотношение
, и при этом выполняется соотношение  . Выведем одну переменную xi из базисного решения, а соответствующий вектор из базиса. Новое решение имеет вид
. Выведем одну переменную xi из базисного решения, а соответствующий вектор из базиса. Новое решение имеет вид 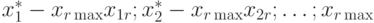 . Данное решение:
. Данное решение: при ограничениях задачи линейного программирования A1x1+A2x2+...+Anxn+An+1xn+1+...+An+mxn+m=A0 имеет вид:
при ограничениях задачи линейного программирования A1x1+A2x2+...+Anxn+An+1xn+1+...+An+mxn+m=A0 имеет вид: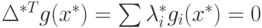 . Функции gi(x) удовлетворяют условию регулярности Слейтера. Тогда:
. Функции gi(x) удовлетворяют условию регулярности Слейтера. Тогда: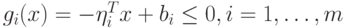 . Известно, что существует множество неотрицательных скаляров {λi} ≥ 0, для которых справедливо соотношение Δf(x*)=Σλiηi(x) = -ΣλiΔgi(x*), i є I. Тогда для входящего вектора справедливо условие:
. Известно, что существует множество неотрицательных скаляров {λi} ≥ 0, для которых справедливо соотношение Δf(x*)=Σλiηi(x) = -ΣλiΔgi(x*), i є I. Тогда для входящего вектора справедливо условие: