Определить напряжение 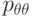 в длинной круглой трубе с внутренним
в длинной круглой трубе с внутренним  и внешним
и внешним  радиусами при плоской деформации, если температура внутри равна
радиусами при плоской деформации, если температура внутри равна 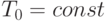 , снаружи
, снаружи 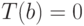 , а ее внешняя и внутренняя поверхности свободны от напряжений
, а ее внешняя и внутренняя поверхности свободны от напряжений
(Отметьте один правильный вариант ответа.)
Варианты ответа
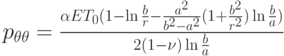 (Верный ответ)
(Верный ответ)



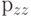 в длинной круглой трубе с внутренним
в длинной круглой трубе с внутренним 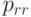 в длинной круглой трубе с внутренним
в длинной круглой трубе с внутренним 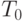 внутри полости постоянна, а температура снаружи равна нулю. Предварительно найти распределение температуры в среде. Внешняя поверхность шара и поверхность полости свободны от напряжений
внутри полости постоянна, а температура снаружи равна нулю. Предварительно найти распределение температуры в среде. Внешняя поверхность шара и поверхность полости свободны от напряжений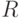 и постоянной толщины температура меняется от центра к периферии по закону
и постоянной толщины температура меняется от центра к периферии по закону  . Все поверхности диска свободны от напряжений, толщина мала, так что напряженное состояние можно считать плоским. Определить напряжение
. Все поверхности диска свободны от напряжений, толщина мала, так что напряженное состояние можно считать плоским. Определить напряжение 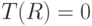
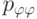 в упругом шаре радиуса
в упругом шаре радиуса  , называется всесторонним сжатием. Коэффициент пропорциональности между
, называется всесторонним сжатием. Коэффициент пропорциональности между  и относительным изменением объема
и относительным изменением объема 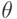 называется модулем объемного сжатия
называется модулем объемного сжатия 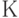 . Найти выражение для
. Найти выражение для 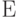 и
и 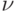
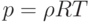 ,
,  , протекает сквозь поверхность разрыва, на которой нет внешних притоков массы, импульса и энергии. Считая потоки тепла
, протекает сквозь поверхность разрыва, на которой нет внешних притоков массы, импульса и энергии. Считая потоки тепла 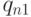 и
и 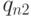 равными нулю (адиабатичность), а значения
равными нулю (адиабатичность), а значения 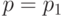 ,
, 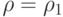 по одну сторону поверхности разрыва известными, найти изменение энтропии
по одну сторону поверхности разрыва известными, найти изменение энтропии  как функцию
как функцию 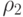
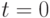 характеристики течения
характеристики течения 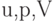 кусочно-постоянны и в области
кусочно-постоянны и в области  (
( ) равны
) равны  , а в области
, а в области  (
(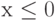 ) —
) —  . Значения
. Значения  в областях
в областях 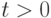 автомодельным?
автомодельным? как функцию
как функцию 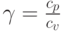 )
)