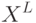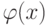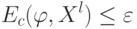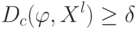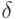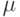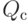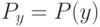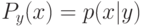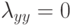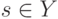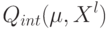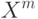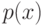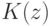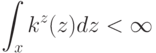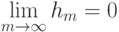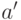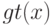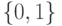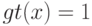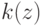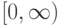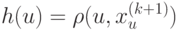Машинное обучение

<<- Назад к вопросам

Выберите, что подходит под определение коэффициента разнообразия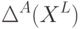
$\Delta^A(X^L)$
множества алгоритмов А на выборке
?

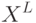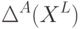
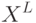
(Отметьте один правильный вариант ответа.)

Варианты ответа

параметры допускающие ошибки на одних и тех же объектах

I(a, X_i)=I(a', X_i)

для всех

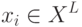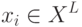
$x_i \in X^L$

;

индикатор ошибки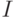

и числа

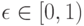$\epsilon \in [0,1)$

, для которых справедлива оценка

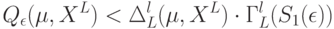$Q_{\epsilon}(\mu, X^L) < \Delta_L^l(\mu, X^L) \cdot Г_L^l(S_1(\epsilon))$

;

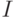
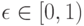
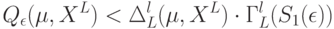
число классов эквивалентности, индуцируемых на множестве А отношением неразличимости алгоритмов на выборке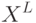

X^L

(Верный ответ)

Похожие вопросы

Какая оценка справедлива для функции роста, если множество А конечно, а число алгоритмов, попарно неразличимы на выборке

X^L

?

Перейти

Как будет называться предикат

$\varphi(x)$

, если

$E_c(\varphi,X^l) \le \varepsilon$

и

$D_c(\varphi, X^l) \ge \delta$

при заданных достаточно малом

$\varepsilon$

и достаточно большом

$\delta$

из отрезка [0,1]?

Перейти

Как будет выглядеть формула вероятности ошибки в интерпретации обобщающей способности метода

$\mu$

, если взять матожидание по выборке

X^l

от функционала

Q_с

?

Перейти

Если известны

P_y = P(y)

и

P_y(x) = p(x|y)

, и

$\lambda_{yy} = 0$

, а

$\lambda_{ys} = \lambda_y$

для всех

,

$s \in Y$

, то минимум среднего риска

R(a)

достигается при:

Перейти

Функционал

$Q_{int}(\mu, X^l)$

, характеризующий качество метода

$\mu$

по обучающей выборке

X^l

называют:

Перейти

Если выполнены условия: 1) выборка

X^m

простая, получена из плотности распределения

p(x)

; 2) ядро

K(z)

непрерывно, его квадрат ограничен:

$\int_x k^z (z)dz<\infty$

; 3) последовательность

h_m

такова, что

$\lim_{\limits {m \to \infty}} h_m = 0$

и

$\lim _{\limits{m \to \infty}} mh_m = \infty$

, тогда:

Перейти

Алгоритмы

и

неразличимы на выборке

X^l

, если:

Перейти

Если в корректирующей операции

$b(x) = F(b_1(x),g_1(x),...,b_r(x), g_r(x)) = \sum_{t=1}^T gt(x) b_t(x)$

функция

gt(x)

принимает только два значения

$\{0,1\}$

, то множество всех

$x \in X$

, для которых

gt(x) = 1

, называется:

Перейти

Какой получится алгоритм, если ввести функцию ядра

k(z)

невозрастающую на

$[0, \infty)$

и положив

$w(i,u)=k(\frac{1}{h} \rho(u, x_u^{(i)}))$

в формуле

$a(u;X^l) = \arg \max_{y \in Y} Г_y(u;X^l)$

?

Перейти

Какой получится алгоритм, если

определить как наибольшее число, при котором ровно

ближайших соседей объекта

получают нулевые веса:

$h(u)=\rho(u,x_u^{(k+1)})$

.

Перейти