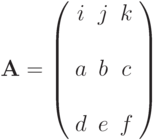Введение в проективную геометрию для школьников - ответы
Количество вопросов - 72
Уравнение вида ax+by+c=0 на плоскости задает
На проективной плоскости через две точки можно провести
Параллельные прямые на проективной плоскости
Точка с координатами (1,0,0) задает на проективной плоскости z=1 точку
Скалярное произведение векторов - это
Верно ли утверждение: любой точке (x:y:z) трехмерного простарнства можно поставить в соответствие точку на проективной плоскости?
Для сокращения времени вычислений, их агрегирования и упрощения в операциях поворота объекта на некоторый угол, сдвига на некоторый вектор и др. используются
Совокупность всех бесконечно удаленных точек плоскости называется
Над векторами недопустима операция
Прямую можно провести через
Векторное произведение векторов - это
Решение системы уравнений, задающих две прямые на плоскости, является
Прямая y=5x+2 в проективных координатах запишется как
Множество точек пересечения двух плоскостей является
Определитель матрицыгде i, j, k - единичные векторы, (a,b,c), (d,e,f) - координаты векторов x и z соответственно, является
Для проведения касательных к окружности, проведенных из одной точки, достаточно знать
Если первый вектор задается координатами (1,2,3), а второй - (4,5,6), то их скалярное произведение равно:
Модуль векторного произведения двух векторов равен
Плоскость, дополненная бесконечно удаленной прямой, называется
Совокупность всех бесконечно удаленных точек пространства называется
Матрица, осуществляющая поворот точки на некоторый угол, называется
Точке (5,6) на проективной плоскости z=1 в евклидовом пространсве соответствует точка
Уравнение прямой в R3 имеет вид:
Если прямые пересекаются в точке, то для нахождения ее координат необходимо знать уравнения минимум
Допустимыми операциями над векторами являются
Число, равное произведению модулей двух векторов на косинус угла между ними, называется
Результат векторного произведения векторов
Определение правой тройки векторов необходимо при вычислении
Определитель матрицыгде i, j, k - единичные векторы, (a,b,c), (d,e,f) - координаты векторов x и z соответственно, является
Две плоскости в проективной геометрии пересекаются по
Проективной прямой называется:
Точке (2,4,6) обычного евклидова пространства на проективной плоскости z=2 соответствует точка
Верно ли утверждение: любой паре (x:y) на проективной плоскости можно поставить в соответствие набор, описывающий точку трехмерного пространства?
Изображение бесконечно удаленной точки на плоскости в двумерном декартовом пространстве
При построении поляра вычисляется
Бесконечно удаленной прямой называется
Если скалярное произведение векторов равно нулю, то вектора
Прямая, дополненная бесконечно удаленной точкой, называется
В наборе чисел (a,b,c), задающем вектор в пространстве R3, каждое число является
В проективной геометрии в дополнение к операциям аналитической геометрии, с помощью матрицы поворота осуществляется
Тройка чисел, характеризующая точку трехмерного евклидова пространства, в которой первая координата умножена на 4, задает на проективной плоскости
Прямой 5x+y-3=0 на проективной плоскости соответствует набор
Пространство, дополненное бесконечно удаленной плоскостью, называется
Множество точек В, таких, что скалярное произведение векторов с концами в этих точках, а началами в центре окружности, и произвольного вектора, выходящего из центра окружности, равно R2, называется
Уравнение прямой на плоскости имеет вид:
Набору чисел (a1,a2,a3) на проективной плоскости соответствует точка
В проективной геометрии в пространстве не существует понятия
Векторное произведение двух векторов равно
Бесконечно удаленные точки непараллельных прямых
Точке на проективной плоскости z=1 с координатами (x,y) в обычном трехмерном пространстве соответствует точка
Через бесконечно удаленную точку и обычную точку трехмерного евклидова пространства
Если длина первого вектора равна 2, длина второго равна 3, а косинус угла между векторами равен 0,5, то скалярное произведение векторов равно
Набор чисел (c:b:a) на проективной плоскости в координатах аналитической геометрии задает прямую
Выражению "результат векторного произведения векторов" соответствует понятие:
Точке (3,2,3) евклидова пространства R3 на проективной плоскости z=3 соответствует точка
Использование матриц в операциях поворота объекта на некоторый угол, сдвига на некоторый вектор обусловлено
На проективной плоскости одну общую бесконечно удаленную точку имеют
Бесконечно удаленная точка
Верно ли утверждение: координатам точки на проективной плоскости взаимно однозначно соответствуют координаты точки евклидова трехмерного пространства
Проективным пространством называется
В аналитической геометрии существует понятие
Прямая, дополненная бесконечно удаленной точкой, называется
Для нахождения точки пересечения двух прямых ax1+by1+c1=0 и ax2+by2+c2=0 необходимо решить
Для вывода уравнений касательных к окружности, проведенных из данной точки (a,b,c) в проективной геометрии, достаточно
Точка и прямая в проективной геометрии
Каждая плоскость в проективной геометрии содержит
Операция сдвига объекта на некоторый вектор в проективной геометрии осуществляется с помощью
Число, равное сумме попарных произведений координат двух векторов, называется
В проективной геометрии прямая есть
При выполнении операций над объектами, задаваемых матрицами A1... An оптимальным будет
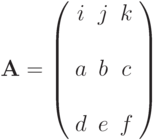 где i, j, k - единичные векторы, (a,b,c), (d,e,f) - координаты векторов x и z соответственно, является
где i, j, k - единичные векторы, (a,b,c), (d,e,f) - координаты векторов x и z соответственно, является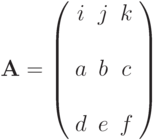
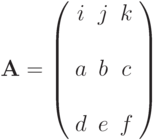 где i, j, k - единичные векторы, (a,b,c), (d,e,f) - координаты векторов x и z соответственно, является
где i, j, k - единичные векторы, (a,b,c), (d,e,f) - координаты векторов x и z соответственно, является