Введение в теорию множеств - ответы
Количество вопросов - 263
Выбрать верное утверждение:
Пусть  . Порядковое число
. Порядковое число  называется разностью
называется разностью  и
и  и обозначается через
и обозначается через  , если
, если 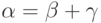 . Выбрать верное утверждение:
. Выбрать верное утверждение:
Выбрать верное утверждение:
Пусть 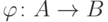 - взаимно однозначное соответствие. Выбрать верное утверждение:
- взаимно однозначное соответствие. Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верные утверждения:
Выбрать верное утверждение:
Через  обозначаются порядковые типы множеств натуральных чисел, целых чисел, рациональных чисел и действительных чисел соответственно с их естественным порядком. Если
обозначаются порядковые типы множеств натуральных чисел, целых чисел, рациональных чисел и действительных чисел соответственно с их естественным порядком. Если  есть порядковый тип множества A , то через
есть порядковый тип множества A , то через  обозначается порядковый тип множества A с двойственным порядком. Выбрать верные утверждения:
обозначается порядковый тип множества A с двойственным порядком. Выбрать верные утверждения:
Мощности произвольных множеств называются кардинальными числами. Выбрать верное утверждение для произвольных кардинальных чисел:
Через  обозначаются порядковые типы множеств натуральных чисел, целых чисел, рациональных чисел и действительных чисел соответственно с их естественным порядком. Если
обозначаются порядковые типы множеств натуральных чисел, целых чисел, рациональных чисел и действительных чисел соответственно с их естественным порядком. Если  есть порядковый тип множества A , то через
есть порядковый тип множества A , то через  обозначается порядковый тип множества A с двойственным порядком. Выбрать верное утверждение:
обозначается порядковый тип множества A с двойственным порядком. Выбрать верное утверждение:
Мощности произвольных множеств называются кардинальными числами. Выбрать верное утверждение для произвольных кардинальных чисел:
Пересечение двух множеств A и B состоит из элементов, которые:
Выбрать верное утверждение:
Выбрать верное утверждение:
Пусть A, B, C - конечные множества. Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Если 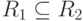 , то:
, то:
Выбрать верные утверждения:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Все множества являются подмножеством некоторого универсального множества U. Выбрать верные утверждения:
Выбрать верные утверждения:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верные утверждения:
Объединение двух множеств A и B состоит из элементов, которые:
Мощностью конечного множества A называют:
Выбрать верные утверждения:
Выбрать верное утверждение:
Выбрать верные утверждения:
Выбрать верные утверждения:
Выбрать верное утверждение:
Выбрать верные утверждения:
Выбрать верные утверждения:
Выбрать верные утверждения:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верные утверждения:
Композиция функций обозначается как:
Инъективную функцию также называют:
Выбрать верное утверждение:
Мощности произвольных множеств называются кардинальными числами. Выбрать верное утверждение:
Мощности произвольных множеств называются кардинальными числами. Выбрать верное утверждение:
Мощности произвольных множеств называются кардинальными числами. Выбрать верное утверждение для произвольных кардинальных чисел:
Выбрать верное утверждение:
Выбрать верное утверждение:
Мощности произвольных множеств называются кардинальными числами. Выбрать верные утверждения для произвольных кардинальных чисел:
Мощности произвольных множеств называются кардинальными числами. Выбрать верное утверждение для произвольных кардинальных чисел:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Если 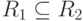 , то:
, то:
Выбрать верное утверждение:
Между множествами можно установить взаимно-однозначное соответствие:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Пусть 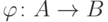 - взаимно однозначное соответствие. Выбрать верное утверждение:
- взаимно однозначное соответствие. Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Через  обозначаются порядковые типы множеств натуральных чисел, целых чисел, рациональных чисел и действительных чисел соответственно с их естественным порядком. Если
обозначаются порядковые типы множеств натуральных чисел, целых чисел, рациональных чисел и действительных чисел соответственно с их естественным порядком. Если  есть порядковый тип множества A , то через
есть порядковый тип множества A , то через  обозначается порядковый тип множества A с двойственным порядком. Выбрать верные утверждения:
обозначается порядковый тип множества A с двойственным порядком. Выбрать верные утверждения:
Выбрать верное утверждение:
Через  обозначаются порядковые типы множеств натуральных чисел, целых чисел, рациональных чисел и действительных чисел соответственно с их естественным порядком. Если
обозначаются порядковые типы множеств натуральных чисел, целых чисел, рациональных чисел и действительных чисел соответственно с их естественным порядком. Если  есть порядковый тип множества A , то через
есть порядковый тип множества A , то через  обозначается порядковый тип множества A с двойственным порядком. Выбрать верное утверждение:
обозначается порядковый тип множества A с двойственным порядком. Выбрать верное утверждение:
Выбрать верные утверждения:
Пусть 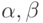 - произвольные порядковые числа. Выбрать верное утверждение:
- произвольные порядковые числа. Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Пусть  . Порядковое число
. Порядковое число  называется разностью
называется разностью  и
и  и обозначается через
и обозначается через  , если
, если 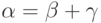 . Выбрать верное утверждение:
. Выбрать верное утверждение:
Выбрать верные утверждения:
Выбрать верное утверждение:
Выбрать верное утверждение:
Мощности произвольных множеств называются кардинальными числами. Выбрать верное утверждение для произвольных кардинальных чисел:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
ООФ  обозначается как:
обозначается как:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Через  обозначаются порядковые типы множеств натуральных чисел, целых чисел, рациональных чисел и действительных чисел соответственно с их естественным порядком. Если
обозначаются порядковые типы множеств натуральных чисел, целых чисел, рациональных чисел и действительных чисел соответственно с их естественным порядком. Если  есть порядковый тип множества A , то через
есть порядковый тип множества A , то через  обозначается порядковый тип множества A с двойственным порядком. Выбрать верное утверждение:
обозначается порядковый тип множества A с двойственным порядком. Выбрать верное утверждение:
Выбрать верное утверждение:
Характеристической функцией множества  называют функцию
называют функцию  , которая:
, которая:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верные утверждения:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верные утверждения:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верные утверждения:
Выбрать верное утверждение:
Выбрать верные утверждения:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Множество бесконечных последовательностей нулей и единиц:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Мощности произвольных множеств называются кардинальными числами. Выбрать верное утверждение для произвольных кардинальных чисел:
Если 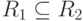 , то:
, то:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Через  обозначаются порядковые типы множеств натуральных чисел, целых чисел, рациональных чисел и действительных чисел соответственно с их естественным порядком. Если
обозначаются порядковые типы множеств натуральных чисел, целых чисел, рациональных чисел и действительных чисел соответственно с их естественным порядком. Если  есть порядковый тип множества A , то через
есть порядковый тип множества A , то через  обозначается порядковый тип множества A с двойственным порядком. Выбрать верные утверждения:
обозначается порядковый тип множества A с двойственным порядком. Выбрать верные утверждения:
Выбрать верное утверждение:
Через  обозначаются порядковые типы множеств натуральных чисел, целых чисел, рациональных чисел и действительных чисел соответственно с их естественным порядком. Если
обозначаются порядковые типы множеств натуральных чисел, целых чисел, рациональных чисел и действительных чисел соответственно с их естественным порядком. Если  есть порядковый тип множества A , то через
есть порядковый тип множества A , то через  обозначается порядковый тип множества A с двойственным порядком. Выбрать верное утверждение:
обозначается порядковый тип множества A с двойственным порядком. Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верные утверждения:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Через  обозначаются порядковые типы множеств натуральных чисел, целых чисел, рациональных чисел и действительных чисел соответственно с их естественным порядком. Если
обозначаются порядковые типы множеств натуральных чисел, целых чисел, рациональных чисел и действительных чисел соответственно с их естественным порядком. Если  есть порядковый тип множества A , то через
есть порядковый тип множества A , то через  обозначается порядковый тип множества A с двойственным порядком. Порядковые числа:
обозначается порядковый тип множества A с двойственным порядком. Порядковые числа:  удовлетворяют условиям:
удовлетворяют условиям:
Выбрать верное утверждение:
Выбрать верные утверждения:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Мощности произвольных множеств называются кардинальными числами. Выбрать верные утверждения для произвольных кардинальных чисел:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верные утверждения:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Между множествами можно установить взаимно-однозначное соответствие:
Выбрать верное утверждение:
Следующие множества являются вполне упорядоченными:
Выбрать верное утверждение:
Симметрическая разность  двух множеств A и B состоит из элементов, которые:
двух множеств A и B состоит из элементов, которые:
Выбрать верное утверждение:
Выбрать верные утверждения:
Выбрать верные утверждения:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Декартово произведение множеств A и B обозначается:
Выбрать верное утверждение:
Мощности произвольных множеств называются кардинальными числами. Выбрать верные утверждения для произвольных кардинальных чисел:
Между множествами можно установить взаимно-однозначное соответствие:
Выбрать верное утверждение:
Выбрать верное утверждение:
Пусть 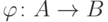 - взаимно однозначное соответствие. Выбрать верное утверждение:
- взаимно однозначное соответствие. Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Через  обозначаются порядковые типы множеств натуральных чисел, целых чисел, рациональных чисел и действительных чисел соответственно с их естественным порядком. Если
обозначаются порядковые типы множеств натуральных чисел, целых чисел, рациональных чисел и действительных чисел соответственно с их естественным порядком. Если  есть порядковый тип множества A , то через
есть порядковый тип множества A , то через  обозначается порядковый тип множества A с двойственным порядком. Выбрать верное утверждение:
обозначается порядковый тип множества A с двойственным порядком. Выбрать верное утверждение:
Через  обозначаются порядковые типы множеств натуральных чисел, целых чисел, рациональных чисел и действительных чисел соответственно с их естественным порядком. Если
обозначаются порядковые типы множеств натуральных чисел, целых чисел, рациональных чисел и действительных чисел соответственно с их естественным порядком. Если  есть порядковый тип множества A , то через
есть порядковый тип множества A , то через  обозначается порядковый тип множества A с двойственным порядком. Выбрать верное утверждение:
обозначается порядковый тип множества A с двойственным порядком. Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Пусть  . Порядковое число
. Порядковое число  называется разностью
называется разностью  и
и  и обозначается через
и обозначается через  , если
, если 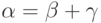 . Выбрать верное утверждение:
. Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Мощность множества A обозначают:
Выбрать верные утверждения:
Выбрать верные утверждения:
Выбрать верное утверждение:
Через  обозначаются порядковые типы множеств натуральных чисел, целых чисел, рациональных чисел и действительных чисел соответственно с их естественным порядком. Если
обозначаются порядковые типы множеств натуральных чисел, целых чисел, рациональных чисел и действительных чисел соответственно с их естественным порядком. Если  есть порядковый тип множества A , то через
есть порядковый тип множества A , то через  обозначается порядковый тип множества A с двойственным порядком. Порядковые числа:
обозначается порядковый тип множества A с двойственным порядком. Порядковые числа:  удовлетворяют условиям:
удовлетворяют условиям:
Выбрать верные утверждения:
>Все множества являются подмножеством некоторого универсального множества U. Выбрать верные утверждения:
Выбрать верные утверждения:
Cюръективную функцию также называют:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Через  обозначаются порядковые типы множеств натуральных чисел, целых чисел, рациональных чисел и действительных чисел соответственно с их естественным порядком. Если
обозначаются порядковые типы множеств натуральных чисел, целых чисел, рациональных чисел и действительных чисел соответственно с их естественным порядком. Если  есть порядковый тип множества A , то через
есть порядковый тип множества A , то через  обозначается порядковый тип множества A с двойственным порядком. Выбрать верное утверждение:
обозначается порядковый тип множества A с двойственным порядком. Выбрать верное утверждение:
Выбрать верное утверждение:
Пусть  . Порядковое число
. Порядковое число  называется разностью
называется разностью  и
и  и обозначается через
и обозначается через  , если
, если 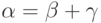 . Выбрать верное утверждение:
. Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верные утверждения:
Выбрать верное утверждение:
Через  обозначаются порядковые типы множеств натуральных чисел, целых чисел, рациональных чисел и действительных чисел соответственно с их естественным порядком. Если
обозначаются порядковые типы множеств натуральных чисел, целых чисел, рациональных чисел и действительных чисел соответственно с их естественным порядком. Если  есть порядковый тип множества A , то через
есть порядковый тип множества A , то через  обозначается порядковый тип множества A с двойственным порядком. Выбрать верное утверждение:
обозначается порядковый тип множества A с двойственным порядком. Выбрать верное утверждение:
Пусть A, B, C - конечные множества. Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Через  обозначаются порядковые типы множеств натуральных чисел, целых чисел, рациональных чисел и действительных чисел соответственно с их естественным порядком. Если
обозначаются порядковые типы множеств натуральных чисел, целых чисел, рациональных чисел и действительных чисел соответственно с их естественным порядком. Если  есть порядковый тип множества A , то через
есть порядковый тип множества A , то через  обозначается порядковый тип множества A с двойственным порядком. Выбрать верное утверждение:
обозначается порядковый тип множества A с двойственным порядком. Выбрать верное утверждение:
Пусть 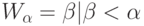 , где
, где  и
и  - порядковые числа, тогда:
- порядковые числа, тогда:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение для непустых множеств:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верное утверждение:
Разность A\B двух множеств A и B состоит из элементов, которые:
Все множества являются подмножеством некоторого универсального множества U. Выбрать верное утверждение:
Выбрать верные утверждения:
Выбрать верное утверждение:
Выбрать верное утверждение:
Выбрать верные утверждения:

 . Порядковое число
. Порядковое число  называется разностью
называется разностью  и
и  и обозначается через
и обозначается через  , если
, если 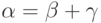 . Выбрать верное утверждение:
. Выбрать верное утверждение: обозначаются порядковые типы множеств натуральных чисел, целых чисел, рациональных чисел и действительных чисел соответственно с их естественным порядком. Если
обозначаются порядковые типы множеств натуральных чисел, целых чисел, рациональных чисел и действительных чисел соответственно с их естественным порядком. Если  есть порядковый тип множества A , то через
есть порядковый тип множества A , то через  обозначается порядковый тип множества A с двойственным порядком. Выбрать верные утверждения:
обозначается порядковый тип множества A с двойственным порядком. Выбрать верные утверждения: обозначаются порядковые типы множеств натуральных чисел, целых чисел, рациональных чисел и действительных чисел соответственно с их естественным порядком. Если
обозначаются порядковые типы множеств натуральных чисел, целых чисел, рациональных чисел и действительных чисел соответственно с их естественным порядком. Если  есть порядковый тип множества A , то через
есть порядковый тип множества A , то через  обозначается порядковый тип множества A с двойственным порядком. Выбрать верное утверждение:
обозначается порядковый тип множества A с двойственным порядком. Выбрать верное утверждение: обозначаются порядковые типы множеств натуральных чисел, целых чисел, рациональных чисел и действительных чисел соответственно с их естественным порядком. Если
обозначаются порядковые типы множеств натуральных чисел, целых чисел, рациональных чисел и действительных чисел соответственно с их естественным порядком. Если  есть порядковый тип множества A , то через
есть порядковый тип множества A , то через  обозначается порядковый тип множества A с двойственным порядком. Выбрать верные утверждения:
обозначается порядковый тип множества A с двойственным порядком. Выбрать верные утверждения: обозначаются порядковые типы множеств натуральных чисел, целых чисел, рациональных чисел и действительных чисел соответственно с их естественным порядком. Если
обозначаются порядковые типы множеств натуральных чисел, целых чисел, рациональных чисел и действительных чисел соответственно с их естественным порядком. Если  есть порядковый тип множества A , то через
есть порядковый тип множества A , то через  обозначается порядковый тип множества A с двойственным порядком. Выбрать верное утверждение:
обозначается порядковый тип множества A с двойственным порядком. Выбрать верное утверждение: . Порядковое число
. Порядковое число  называется разностью
называется разностью  и
и  и обозначается через
и обозначается через  , если
, если 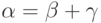 . Выбрать верное утверждение:
. Выбрать верное утверждение: обозначаются порядковые типы множеств натуральных чисел, целых чисел, рациональных чисел и действительных чисел соответственно с их естественным порядком. Если
обозначаются порядковые типы множеств натуральных чисел, целых чисел, рациональных чисел и действительных чисел соответственно с их естественным порядком. Если  есть порядковый тип множества A , то через
есть порядковый тип множества A , то через  обозначается порядковый тип множества A с двойственным порядком. Выбрать верное утверждение:
обозначается порядковый тип множества A с двойственным порядком. Выбрать верное утверждение: обозначаются порядковые типы множеств натуральных чисел, целых чисел, рациональных чисел и действительных чисел соответственно с их естественным порядком. Если
обозначаются порядковые типы множеств натуральных чисел, целых чисел, рациональных чисел и действительных чисел соответственно с их естественным порядком. Если  есть порядковый тип множества A , то через
есть порядковый тип множества A , то через  обозначается порядковый тип множества A с двойственным порядком. Выбрать верные утверждения:
обозначается порядковый тип множества A с двойственным порядком. Выбрать верные утверждения: обозначаются порядковые типы множеств натуральных чисел, целых чисел, рациональных чисел и действительных чисел соответственно с их естественным порядком. Если
обозначаются порядковые типы множеств натуральных чисел, целых чисел, рациональных чисел и действительных чисел соответственно с их естественным порядком. Если  есть порядковый тип множества A , то через
есть порядковый тип множества A , то через  обозначается порядковый тип множества A с двойственным порядком. Выбрать верное утверждение:
обозначается порядковый тип множества A с двойственным порядком. Выбрать верное утверждение: обозначаются порядковые типы множеств натуральных чисел, целых чисел, рациональных чисел и действительных чисел соответственно с их естественным порядком. Если
обозначаются порядковые типы множеств натуральных чисел, целых чисел, рациональных чисел и действительных чисел соответственно с их естественным порядком. Если  есть порядковый тип множества A , то через
есть порядковый тип множества A , то через  обозначается порядковый тип множества A с двойственным порядком. Порядковые числа:
обозначается порядковый тип множества A с двойственным порядком. Порядковые числа:  удовлетворяют условиям:
удовлетворяют условиям: обозначаются порядковые типы множеств натуральных чисел, целых чисел, рациональных чисел и действительных чисел соответственно с их естественным порядком. Если
обозначаются порядковые типы множеств натуральных чисел, целых чисел, рациональных чисел и действительных чисел соответственно с их естественным порядком. Если  есть порядковый тип множества A , то через
есть порядковый тип множества A , то через  обозначается порядковый тип множества A с двойственным порядком. Выбрать верное утверждение:
обозначается порядковый тип множества A с двойственным порядком. Выбрать верное утверждение: обозначаются порядковые типы множеств натуральных чисел, целых чисел, рациональных чисел и действительных чисел соответственно с их естественным порядком. Если
обозначаются порядковые типы множеств натуральных чисел, целых чисел, рациональных чисел и действительных чисел соответственно с их естественным порядком. Если  есть порядковый тип множества A , то через
есть порядковый тип множества A , то через  обозначается порядковый тип множества A с двойственным порядком. Выбрать верное утверждение:
обозначается порядковый тип множества A с двойственным порядком. Выбрать верное утверждение: . Порядковое число
. Порядковое число  называется разностью
называется разностью  и
и  и обозначается через
и обозначается через  , если
, если 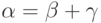 . Выбрать верное утверждение:
. Выбрать верное утверждение: обозначаются порядковые типы множеств натуральных чисел, целых чисел, рациональных чисел и действительных чисел соответственно с их естественным порядком. Если
обозначаются порядковые типы множеств натуральных чисел, целых чисел, рациональных чисел и действительных чисел соответственно с их естественным порядком. Если  есть порядковый тип множества A , то через
есть порядковый тип множества A , то через  обозначается порядковый тип множества A с двойственным порядком. Порядковые числа:
обозначается порядковый тип множества A с двойственным порядком. Порядковые числа:  удовлетворяют условиям:
удовлетворяют условиям: обозначаются порядковые типы множеств натуральных чисел, целых чисел, рациональных чисел и действительных чисел соответственно с их естественным порядком. Если
обозначаются порядковые типы множеств натуральных чисел, целых чисел, рациональных чисел и действительных чисел соответственно с их естественным порядком. Если  есть порядковый тип множества A , то через
есть порядковый тип множества A , то через  обозначается порядковый тип множества A с двойственным порядком. Выбрать верное утверждение:
обозначается порядковый тип множества A с двойственным порядком. Выбрать верное утверждение: . Порядковое число
. Порядковое число  называется разностью
называется разностью  и
и  и обозначается через
и обозначается через  , если
, если 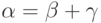 . Выбрать верное утверждение:
. Выбрать верное утверждение: обозначаются порядковые типы множеств натуральных чисел, целых чисел, рациональных чисел и действительных чисел соответственно с их естественным порядком. Если
обозначаются порядковые типы множеств натуральных чисел, целых чисел, рациональных чисел и действительных чисел соответственно с их естественным порядком. Если  есть порядковый тип множества A , то через
есть порядковый тип множества A , то через  обозначается порядковый тип множества A с двойственным порядком. Выбрать верное утверждение:
обозначается порядковый тип множества A с двойственным порядком. Выбрать верное утверждение: обозначаются порядковые типы множеств натуральных чисел, целых чисел, рациональных чисел и действительных чисел соответственно с их естественным порядком. Если
обозначаются порядковые типы множеств натуральных чисел, целых чисел, рациональных чисел и действительных чисел соответственно с их естественным порядком. Если  есть порядковый тип множества A , то через
есть порядковый тип множества A , то через  обозначается порядковый тип множества A с двойственным порядком. Выбрать верное утверждение:
обозначается порядковый тип множества A с двойственным порядком. Выбрать верное утверждение: