База ответов ИНТУИТ

Математический анализ

<<- Назад к вопросам

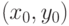Пусть (x_0,y_0) точка экстремума функции 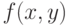f(x,y) при условии 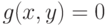g(x,y)=0. Тогда

(Ответ считается верным, если отмечены все правильные варианты ответов.)
Варианты ответа
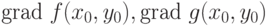\text{grad }f(x_0,y_0),\text{grad }g(x_0,y_0) линейно зависимы(Верный ответ)
\text{grad }f(x_0,y_0)\neq \lambda\cdot\text{grad }g(x_0,y_0)
\text{grad }f(x_0,y_0)=\lambda\cdot\text{grad }g(x_0,y_0)(Верный ответ)
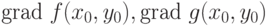\text{grad }f(x_0,y_0),\text{grad }g(x_0,y_0) линейно независимы
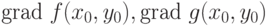\text{grad }f(x_0,y_0),\text{grad }g(x_0,y_0) перпендикулярны
Похожие вопросы
Пусть (x_0,y_0) точка экстремума функции f(x,y) при условии g(x,y)=0. Тогда линия уровня f(x,y)=f(x_0,y_0) пересекает кривую L=\{(x,y):\quad g(x,y)=0\} под углом
Пусть (x_0,y_0) не является точкой экстремума функции f(x,y) при условии g(x,y)=0. Тогда линия уровня f(x,y)=f(x_0,y_0) пересекает кривую L=\{(x,y):\quad g(x,y)=0\} под углом
Пусть (x_0,y_0) точка экстремума дифференцируемой функции f(x,y). Тогда
Пусть (x_0,y_0) - особая точка для дифференцируемой функции f(x,y). Какое условие является достаточным для того, чтобы (x_0,y_0) была точкой локального максимума:
Пусть (x_0,y_0) - особая точка для дифференцируемой функции f(x,y). Какое условие является достаточным для того, чтобы (x_0,y_0) была точкой локального минимума:
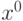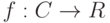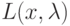Пусть x^0 - точка условного экстремума функции f:C\rightarrow R и задана функция Лагранжа L(x,\lambda). Тогда
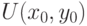Точка (x_0,y_0) не является точкой локального максимума для функции f(x,y), если для любой окрестности U(x_0,y_0):
Точка (x_0,y_0) является точкой локального максимума для функции f(x,y), если существует окрестность U(x_0,y_0):
Точка (x_0,y_0) является точкой локального минимума для функции f(x,y), если существует окрестность U(x_0,y_0):
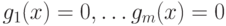Пусть задана функция f:C\rightarrow R при условии g_1(x)=0,\ldots g_m(x)=0. Пусть задана функция Лагранжа L(x,\lambda). Тогда особая точка x^0 будет точкой условного локального максимума, если для любого допустимого сдвига