Пусть  - множество сходимости ряда
- множество сходимости ряда 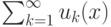 . Функция
. Функция  является суммой ряда. Тогда она
является суммой ряда. Тогда она
(Ответ считается верным, если отмечены все правильные варианты ответов.)
Варианты ответа
разрывна на  , если
, если 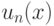 разрывна на
разрывна на 
 , если
, если 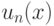 разрывна на
разрывна на 
определена на множестве 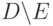
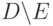
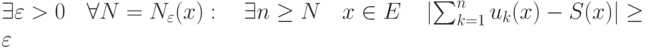
определена на множестве  (Верный ответ)
(Верный ответ)
 (Верный ответ)
(Верный ответ)
непрерывна на  , если
, если 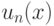 непрерывны на
непрерывны на 
 , если
, если 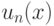 непрерывны на
непрерывны на 
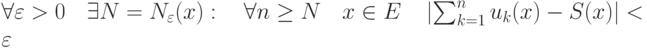 (Верный ответ)
(Верный ответ)

 - множество сходимости последовательности
- множество сходимости последовательности  . Функция
. Функция  является пределом последовательности
является пределом последовательности 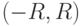 интервал сходимости степенного ряда
интервал сходимости степенного ряда 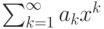 . Тогда множеством непрерывности суммы ряда является множество
. Тогда множеством непрерывности суммы ряда является множество![\overline{\lim_{n\rightarrow\infty}}\frac{1}{\sqrt[n]{|a_n|}}=+\infty](https://intuit.ru//sites/default/files/tex_cache/e792e0d067a9f672402e867f587bbf71.png) , то интервал сходимости ряда
, то интервал сходимости ряда 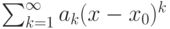
![\overline{\lim_{n\rightarrow\infty}}\frac{1}{\sqrt[n]{|a_n|}}=0](https://intuit.ru//sites/default/files/tex_cache/ddf35819a71b0020954b73df847aa2ca.png) , то интервал сходимости ряда
, то интервал сходимости ряда 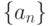 и
и 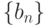 сходятся и
сходятся и  . Тогда последовательность
. Тогда последовательность  сходится и ее предел равен
сходится и ее предел равен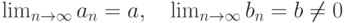 . Тогда последовательность
. Тогда последовательность  сходится и ее предел равен
сходится и ее предел равен .Тогда последовательность
.Тогда последовательность  сходится и ее предел равен
сходится и ее предел равен