Пусть для функции 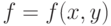 в точке
в точке 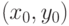 существует градиент
существует градиент  . Тогда
. Тогда
(Ответ считается верным, если отмечены все правильные варианты ответов.)
Варианты ответа
![\text{grad }f(x_0,y_0)=[\frac{\partial f}{\partial x}(x_0,y_0),\frac{\partial f}{\partial y}(x_0,y_0)]](https://intuit.ru//sites/default/files/tex_cache/307df7f6174b1ce1ca3172449fc2ad9a.png) (Верный ответ)
(Верный ответ)
![\text{grad }f(x_0,y_0)=[\frac{\partial f}{\partial y}(x_0,y_0),\frac{\partial f}{\partial x}(x_0,y_0)]](https://intuit.ru//sites/default/files/tex_cache/116029c5fb5a5f2bd4c2dc8e96476b58.png)
градиент направлен по касательной к линии уровня 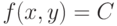
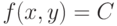
градиент перпендикулярен к линии уровня 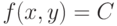 (Верный ответ)
(Верный ответ)
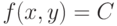 (Верный ответ)
(Верный ответ)
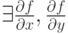 в точке
в точке 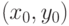 (Верный ответ)
(Верный ответ)

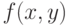 при условии
при условии 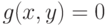 . Тогда линия уровня
. Тогда линия уровня  пересекает кривую
пересекает кривую  под углом
под углом . Тогда
. Тогда 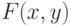 непрерывна в окрестности точки
непрерывна в окрестности точки 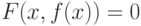 . Пусть существует единственная неявная функция
. Пусть существует единственная неявная функция 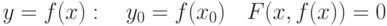 . Тогда
. Тогда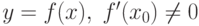 обратима в окрестности точки
обратима в окрестности точки  и
и 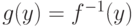 - обратная функция. Тогда производная
- обратная функция. Тогда производная 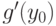 в точке
в точке 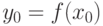 равна
равна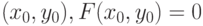 и
и 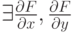 непрерывные в окрестности
непрерывные в окрестности 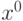 является точкой локального максимума для функции
является точкой локального максимума для функции 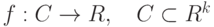 при условиях
при условиях 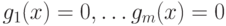 , если для
, если для 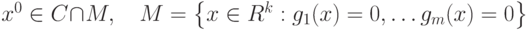 существует окрестность
существует окрестность 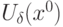 :
: