В условиях теоремы Лагранжа точка с: 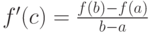
(Ответ считается верным, если отмечены все правильные варианты ответов.)
Варианты ответа
хотя бы одна(Верный ответ)
единственная
принадлежит интервалу 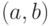 (Верный ответ)
(Верный ответ)
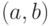 (Верный ответ)
(Верный ответ)
лежит вне отрезка ![[a,b]](https://intuit.ru//sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png)
![[a,b]](https://intuit.ru//sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png)
совпадает с концами отрезка  или
или 
 или
или 

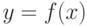 , в которой касательная
, в которой касательная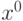 является точкой локального максимума для функции
является точкой локального максимума для функции 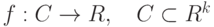 при условиях
при условиях 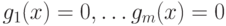 , если для
, если для 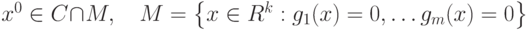 существует окрестность
существует окрестность 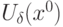 :
: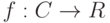 и задана функция Лагранжа
и задана функция Лагранжа 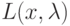 . Тогда
. Тогда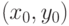 точка экстремума функции
точка экстремума функции 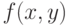 при условии
при условии 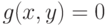 . Тогда линия уровня
. Тогда линия уровня  пересекает кривую
пересекает кривую  под углом
под углом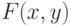 непрерывна в окрестности точки
непрерывна в окрестности точки 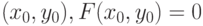 и
и 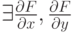 непрерывные в окрестности
непрерывные в окрестности 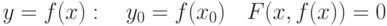 :
: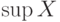 и
и 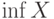 , если множество
, если множество  состоит из элементов, являющихся членами последовательности
состоит из элементов, являющихся членами последовательности 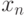 , где
, где 
 для функции
для функции  является точкой разрыва
является точкой разрыва