База ответов ИНТУИТ

Математический анализ

<<- Назад к вопросам

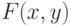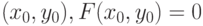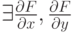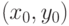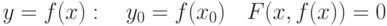Пусть F(x,y) непрерывна в окрестности точки (x_0,y_0),F(x_0,y_0)=0 и \exists\frac{\partial F}{\partial x},\frac{\partial F}{\partial y} непрерывные в окрестности (x_0,y_0). Какие условия достаточны для существования единственной неявной функции y=f(x):\quad y_0=f(x_0)\quad F(x,f(x))=0:

(Отметьте один правильный вариант ответа.)
Варианты ответа
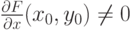
\frac{\partial F}{\partial x}(x_0,y_0)\neq 0
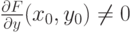\frac{\partial F}{\partial y}(x_0,y_0)\neq 0(Верный ответ)
\frac{\partial F}{\partial y}(x_0,y_0)=0
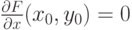
\frac{\partial F}{\partial x}(x_0,y_0)=0
Похожие вопросы
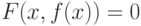Пусть F(x,y) непрерывна в окрестности точки (x_0,y_0) и F(x,f(x))=0. Пусть существует единственная неявная функция y=f(x):\quad y_0=f(x_0)\quad F(x,f(x))=0. Тогда
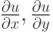Чему равны частные производные \frac{\partial u}{\partial x},\frac{\partial u}{\partial y} функции u=xy^2:
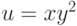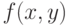Пусть (x_0,y_0) не является точкой экстремума функции f(x,y) при условии 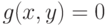g(x,y)=0. Тогда линия уровня f(x,y)=f(x_0,y_0) пересекает кривую L=\{(x,y):\quad g(x,y)=0\} под углом
Пусть (x_0,y_0) точка экстремума функции f(x,y) при условии g(x,y)=0. Тогда линия уровня f(x,y)=f(x_0,y_0) пересекает кривую L=\{(x,y):\quad g(x,y)=0\} под углом
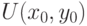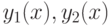Если f(x,y) непрерывна и удовлетворяет условию Липшица в некоторой окрестности U(x_0,y_0) и y_1(x),y_2(x) - решения задачи Коши 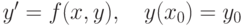y'=f(x,y),\quad y(x_0)=y_0, то
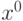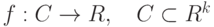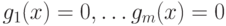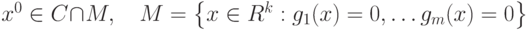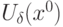Точка x^0 является точкой локального минимума для функции f:C\rightarrow R,\quad C \subset R^k при условиях g_1(x)=0,\ldots g_m(x)=0, если для x^0\in C\cap M,\quad M=\left\{x\in R^k:g_1(x)=0,\ldots g_m(x)=0\right\} существует окрестность U_{\delta}(x^0):
Точка x^0 является точкой локального максимума для функции f:C\rightarrow R,\quad C \subset R^k при условиях g_1(x)=0,\ldots g_m(x)=0, если для x^0\in C\cap M,\quad M=\left\{x\in R^k:g_1(x)=0,\ldots g_m(x)=0\right\} существует окрестность U_{\delta}(x^0):
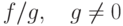Пусть функции f,g:M\rightarrow R. Какие условия достаточны для того, чтобы функция f/g,\quad g\neq 0 была непрерывной в точке x^0 \in M:
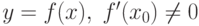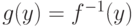Пусть функция y=f(x),\; f'(x_0)\neq 0 обратима в окрестности точки x_0 и g(y)=f^{-1}(y) - обратная функция. Тогда производная 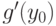g'(y_0) в точке 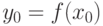y_0=f(x_0) равна
Пусть f(x)=\begin{cases}x^2\sin\frac{1}{x^2},x\neq 0 \\ 0, \phantom{\sin x^2x} x=0\end{cases}. Сколько точек пересечения касательной к графику функции в точке x=0 и графика функции в произвольной окрестности точки (0,0):