Выборка  имеет равномерное распределение
имеет равномерное распределение 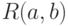 , а выборка
, а выборка  имеет равномерное распределение
имеет равномерное распределение 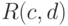 . В каком случае эти выборки будут являться однородными?
. В каком случае эти выборки будут являться однородными?
(Ответ считается верным, если отмечены все правильные варианты ответов.)
Варианты ответа
если 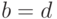
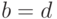
эти выборки неоднородны при любых условиях на параметры их распределений
если 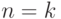
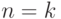
эти выборки являются однородными
если  и
и 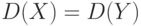 (Верный ответ)
(Верный ответ)
 и
и 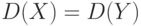 (Верный ответ)
(Верный ответ)
если 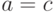 и
и 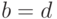 (Верный ответ)
(Верный ответ)
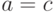 и
и 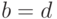 (Верный ответ)
(Верный ответ)
если 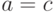
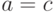

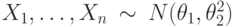 , а выборка
, а выборка 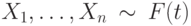 , а выборка
, а выборка 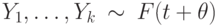 . Для проверки гипотезы
. Для проверки гипотезы 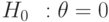 применяют критерий Вилкоксона и критерий Стьюдента. Известно, что распределение
применяют критерий Вилкоксона и критерий Стьюдента. Известно, что распределение 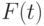 - непрерывное распределение с нулевой медианой. Чему равна нижняя граница
- непрерывное распределение с нулевой медианой. Чему равна нижняя граница 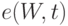 АОЭ (асимптотической относительной эффективности) по Питмену критерия Вилкоксона по отношению к критерию Стьюдента?
АОЭ (асимптотической относительной эффективности) по Питмену критерия Вилкоксона по отношению к критерию Стьюдента?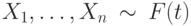 , а выборка
, а выборка  и
и  . Параметры
. Параметры 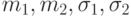 неизвестны. Пусть
неизвестны. Пусть 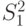 -выборочная дисперсия первой выборки,
-выборочная дисперсия первой выборки, 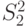 -выборочная дисперсия второй выборки. Какое распределение имеет статистика
-выборочная дисперсия второй выборки. Какое распределение имеет статистика 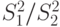 в случае, когда дисперсии первой и второй выборок одинаковы?
в случае, когда дисперсии первой и второй выборок одинаковы?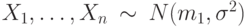 и
и  . Параметры
. Параметры 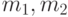 и
и 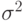 неизвестны. Обозначим
неизвестны. Обозначим 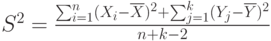 . Какое распределение имеет статистика
. Какое распределение имеет статистика 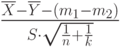 ?
?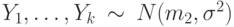 . Параметры
. Параметры 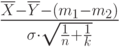 ?
? . В каком случае эти выборки будут являться однородными?
. В каком случае эти выборки будут являться однородными?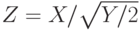 , где случайная величина
, где случайная величина  имеет стандартное нормальное распределение
имеет стандартное нормальное распределение  , а случайная величина
, а случайная величина  имеет распределение хи-квадрат с двумя степенями свободы (
имеет распределение хи-квадрат с двумя степенями свободы ( ). Известно, что
). Известно, что  ?
?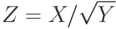 , где случайная величина
, где случайная величина 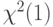 ). Известно, что
). Известно, что 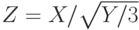 , где случайная величина
, где случайная величина  ). Известно, что
). Известно, что