По выборке 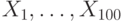 из распределения
из распределения 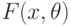 требуется проверить гипотезу о том, что неизвестный параметр
требуется проверить гипотезу о том, что неизвестный параметр 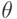 равен 5 против альтернативы о том, что значение параметра
равен 5 против альтернативы о том, что значение параметра 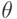 больше 5. Для проверки этой гипотезы применяется некоторый состоятельный критерий. Уровень значимости этого критерия равен 0.05. Функция мощности этого критерия в точке 6 можетпринимать значение:
больше 5. Для проверки этой гипотезы применяется некоторый состоятельный критерий. Уровень значимости этого критерия равен 0.05. Функция мощности этого критерия в точке 6 можетпринимать значение:
(Отметьте один правильный вариант ответа.)
Варианты ответа
0.05
меньше чем 0.05
больше чем 0.05(Верный ответ)

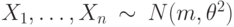 с известным математическим ожиданием
с известным математическим ожиданием  построены доверительные интервалы уровня надежности
построены доверительные интервалы уровня надежности 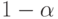 для параметра
для параметра 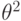 .Обозначим
.Обозначим 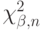 - квантиль уровня
- квантиль уровня  распределения хи-квадрат с
распределения хи-квадрат с  степенями свободы. Какой из представленных интервалов является центральным доверительным интервалом параметра
степенями свободы. Какой из представленных интервалов является центральным доверительным интервалом параметра 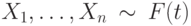 , а выборка
, а выборка 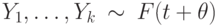 . Для проверки гипотезы
. Для проверки гипотезы 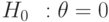 применяют критерий Вилкоксона и критерий Стьюдента. Известно, что распределение
применяют критерий Вилкоксона и критерий Стьюдента. Известно, что распределение 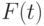 - непрерывное распределение с нулевой медианой. Чему равна нижняя граница
- непрерывное распределение с нулевой медианой. Чему равна нижняя граница 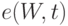 АОЭ (асимптотической относительной эффективности) по Питмену критерия Вилкоксона по отношению к критерию Стьюдента?
АОЭ (асимптотической относительной эффективности) по Питмену критерия Вилкоксона по отношению к критерию Стьюдента?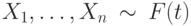 , а выборка
, а выборка 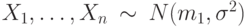 и
и 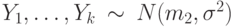 . Проверяется гипотеза
. Проверяется гипотеза  . Для проверки этой гипотезы применяют критерий Вилкоксона и критерий Стьюдента. Чему равна АОЭ (асимптотическая относительная эффективность) по Питмену критерия Вилкоксона по отношению к критерию Стьюдента?
. Для проверки этой гипотезы применяют критерий Вилкоксона и критерий Стьюдента. Чему равна АОЭ (асимптотическая относительная эффективность) по Питмену критерия Вилкоксона по отношению к критерию Стьюдента? . Какие из следующих статистик являются центральными статистиками для
. Какие из следующих статистик являются центральными статистиками для  построены доверительные интервалы уровня надежности
построены доверительные интервалы уровня надежности 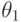 .Обозначим
.Обозначим  - выборочную дисперсию, а
- выборочную дисперсию, а  -квантиль уровня
-квантиль уровня 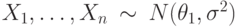 с известной дисперсией
с известной дисперсией 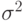 построены доверительные интервалы уровня надежности
построены доверительные интервалы уровня надежности 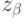 - квантиль стандартного гауссовского распределения уровня
- квантиль стандартного гауссовского распределения уровня  против альтернативы
против альтернативы 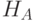 , достаточно знать
, достаточно знать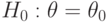 против альтернативной гипотезы
против альтернативной гипотезы