Приближенные и численные методы решения дифференциальных уравнений - ответы
Количество вопросов - 72

 . Начальные условия
. Начальные условия  . Шаг 0,15. В ответе указать значение
. Шаг 0,15. В ответе указать значение  . (Округлить до 3-х знаков после запятой.)
. (Округлить до 3-х знаков после запятой.) . Начальные условия
. Начальные условия  . Шаг 0,05. В ответе указать значение
. Шаг 0,05. В ответе указать значение  . (Округлить до 4-х знаков после запятой.)
. (Округлить до 4-х знаков после запятой.)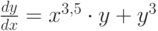 . Начальные условия
. Начальные условия  . Шаг 0,1. В ответе указать значение
. Шаг 0,1. В ответе указать значение  . (Округлить до 4-х знаков после запятой.)
. (Округлить до 4-х знаков после запятой.)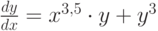 . Начальные условия
. Начальные условия  . Шаг 0,01. В ответе указать значение
. Шаг 0,01. В ответе указать значение  . (Округлить до 3-х знаков после запятой.)
. (Округлить до 3-х знаков после запятой.)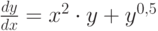 . Начальные условия
. Начальные условия  . Шаг 0,05. В ответе указать значение
. Шаг 0,05. В ответе указать значение  . (Округлить до 4-х знаков после запятой.)
. (Округлить до 4-х знаков после запятой.)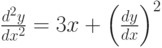 задана краевая задача
задана краевая задача  ;
;  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1,6. чему равно
равна 1,6. чему равно  . В ответе приведите один знак после запятой. Шаг решения методом Эйлера 0,1.
. В ответе приведите один знак после запятой. Шаг решения методом Эйлера 0,1.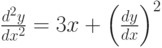 задана краевая задача
задана краевая задача  ;
;  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1,5625. чему равно
равна 1,5625. чему равно  . В ответе приведите один знак после запятой. Шаг решения методом Эйлера 0,1.
. В ответе приведите один знак после запятой. Шаг решения методом Эйлера 0,1.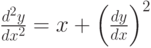 задана краевая задача
задана краевая задача  ;
;  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1. чему равно
равна 1. чему равно  . В ответе приведите один знак после запятой. Шаг решения методом Эйлера 0,1.
. В ответе приведите один знак после запятой. Шаг решения методом Эйлера 0,1.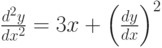 задана краевая задача
задана краевая задача  ;
;  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1,5. чему равно
равна 1,5. чему равно  . В ответе приведите один знак после запятой. Шаг решения методом Эйлера 0,1.
. В ответе приведите один знак после запятой. Шаг решения методом Эйлера 0,1.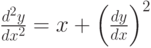 задана краевая задача
задана краевая задача  ;
;  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1,6125. чему равно
равна 1,6125. чему равно  . В ответе приведите один знак после запятой. Шаг решения методом Эйлера 0,1.
. В ответе приведите один знак после запятой. Шаг решения методом Эйлера 0,1.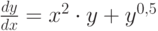 . Начальные условия
. Начальные условия  . Шаг 0,15. В ответе указать значение
. Шаг 0,15. В ответе указать значение  . (Округлить до 4-х знаков после запятой.)
. (Округлить до 4-х знаков после запятой.)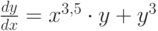 . Начальные условия
. Начальные условия  . Шаг 0,01. В ответе указать значение
. Шаг 0,01. В ответе указать значение  . (Округлить до 4-х знаков после запятой.)
. (Округлить до 4-х знаков после запятой.)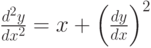 задана краевая задача
задана краевая задача  ;
;  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 2. чему равно
равна 2. чему равно  . В ответе приведите один знак после запятой. Шаг решения методом Эйлера 0,1.
. В ответе приведите один знак после запятой. Шаг решения методом Эйлера 0,1.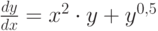 . Начальные условия
. Начальные условия  . Шаг 0,01. В ответе указать значение
. Шаг 0,01. В ответе указать значение  . (Округлить до 3-х знаков после запятой.)
. (Округлить до 3-х знаков после запятой.)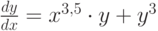 . Начальные условия
. Начальные условия  . Шаг 0,05. В ответе указать значение
. Шаг 0,05. В ответе указать значение  . (Округлить до 3-х знаков после запятой.)
. (Округлить до 3-х знаков после запятой.) . Начальные условия
. Начальные условия  . Шаг 0,01. В ответе указать значение
. Шаг 0,01. В ответе указать значение  . (Округлить до 4-х знаков после запятой.)
. (Округлить до 4-х знаков после запятой.)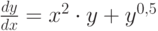 . Начальные условия
. Начальные условия  . Шаг 0,15. В ответе указать значение
. Шаг 0,15. В ответе указать значение  . (Округлить до 4-х знаков после запятой.)
. (Округлить до 4-х знаков после запятой.)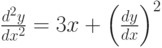 задана краевая задача
задана краевая задача  ;
;  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1,75. чему равно
равна 1,75. чему равно  . В ответе приведите один знак после запятой. Шаг решения методом Эйлера 0,1.
. В ответе приведите один знак после запятой. Шаг решения методом Эйлера 0,1.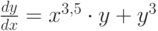 . Начальные условия
. Начальные условия  . Шаг 0,1. В ответе указать значение
. Шаг 0,1. В ответе указать значение  . (Округлить до 4-х знаков после запятой.)
. (Округлить до 4-х знаков после запятой.)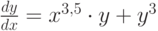 . Начальные условия
. Начальные условия  . Шаг 0,05. В ответе указать значение
. Шаг 0,05. В ответе указать значение  . (Округлить до 3-х знаков после запятой.)
. (Округлить до 3-х знаков после запятой.)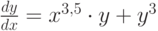 . Начальные условия
. Начальные условия  . Шаг 0,1. В ответе указать значение
. Шаг 0,1. В ответе указать значение  . (Округлить до 3-х знаков после запятой.)
. (Округлить до 3-х знаков после запятой.) . Начальные условия
. Начальные условия  . Шаг 0,1. В ответе указать значение
. Шаг 0,1. В ответе указать значение  . (Округлить до 3-х знаков после запятой.)
. (Округлить до 3-х знаков после запятой.)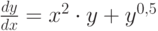 . Начальные условия
. Начальные условия  . Шаг 0,15. В ответе указать значение
. Шаг 0,15. В ответе указать значение  . (Округлить до 3-х знаков после запятой.)
. (Округлить до 3-х знаков после запятой.)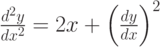 задана краевая задача
задана краевая задача  ;
;  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1,625. чему равно
равна 1,625. чему равно  . В ответе приведите один знак после запятой. Шаг решения методом Эйлера 0,1.
. В ответе приведите один знак после запятой. Шаг решения методом Эйлера 0,1.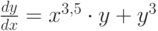 . Начальные условия
. Начальные условия  . Шаг 0,15. В ответе указать значение
. Шаг 0,15. В ответе указать значение  . (Округлить до 3-х знаков после запятой.)
. (Округлить до 3-х знаков после запятой.)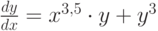 . Начальные условия
. Начальные условия  . Шаг 0,1. В ответе указать значение
. Шаг 0,1. В ответе указать значение  . (Округлить до 3-х знаков после запятой.)
. (Округлить до 3-х знаков после запятой.) . Начальные условия
. Начальные условия  . Шаг 0,05. В ответе указать значение
. Шаг 0,05. В ответе указать значение  . (Округлить до 3-х знаков после запятой.)
. (Округлить до 3-х знаков после запятой.)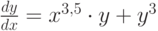 . Начальные условия
. Начальные условия  . Шаг 0,01. В ответе указать значение
. Шаг 0,01. В ответе указать значение  . (Округлить до 3-х знаков после запятой.)
. (Округлить до 3-х знаков после запятой.) . Начальные условия
. Начальные условия  . Шаг 0,1. В ответе указать значение
. Шаг 0,1. В ответе указать значение  . (Округлить до 3-х знаков после запятой.)
. (Округлить до 3-х знаков после запятой.)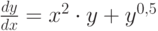 . Начальные условия
. Начальные условия  . Шаг 0,01. В ответе указать значение
. Шаг 0,01. В ответе указать значение  . (Округлить до 3-х знаков после запятой.)
. (Округлить до 3-х знаков после запятой.)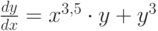 . Начальные условия
. Начальные условия  . Шаг 0,15. В ответе указать значение
. Шаг 0,15. В ответе указать значение  . (Округлить до 4-х знаков после запятой.)
. (Округлить до 4-х знаков после запятой.) . Начальные условия
. Начальные условия  . Шаг 0,1. В ответе указать значение
. Шаг 0,1. В ответе указать значение  . (Округлить до 4-х знаков после запятой.)
. (Округлить до 4-х знаков после запятой.)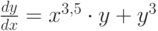 . Начальные условия
. Начальные условия  . Шаг 0,05. В ответе указать значение
. Шаг 0,05. В ответе указать значение  . (Округлить до 4-х знаков после запятой.)
. (Округлить до 4-х знаков после запятой.)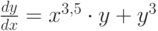 . Начальные условия
. Начальные условия  . Шаг 0,15. В ответе указать значение
. Шаг 0,15. В ответе указать значение  . (Округлить до 4-х знаков после запятой.)
. (Округлить до 4-х знаков после запятой.)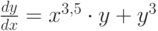 . Начальные условия
. Начальные условия  . Шаг 0,05. В ответе указать значение
. Шаг 0,05. В ответе указать значение  . (Округлить до 4-х знаков после запятой.)
. (Округлить до 4-х знаков после запятой.)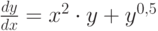 . Начальные условия
. Начальные условия  . Шаг 0,01. В ответе указать значение
. Шаг 0,01. В ответе указать значение  . (Округлить до 4-х знаков после запятой.)
. (Округлить до 4-х знаков после запятой.)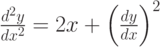 задана краевая задача
задана краевая задача  ;
;  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 2. чему равно
равна 2. чему равно  . В ответе приведите один знак после запятой. Шаг решения методом Эйлера 0,1.
. В ответе приведите один знак после запятой. Шаг решения методом Эйлера 0,1.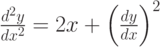 задана краевая задача
задана краевая задача  ;
;  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1. чему равно
равна 1. чему равно  . В ответе приведите один знак после запятой. Шаг решения методом Эйлера 0,1.
. В ответе приведите один знак после запятой. Шаг решения методом Эйлера 0,1.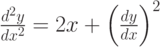 задана краевая задача
задана краевая задача  ;
;  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1,5. чему равно
равна 1,5. чему равно  . В ответе приведите один знак после запятой. Шаг решения методом Эйлера 0,1.
. В ответе приведите один знак после запятой. Шаг решения методом Эйлера 0,1.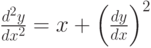 задана краевая задача
задана краевая задача  ;
;  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1,75. чему равно
равна 1,75. чему равно  . В ответе приведите один знак после запятой. Шаг решения методом Эйлера 0,1.
. В ответе приведите один знак после запятой. Шаг решения методом Эйлера 0,1.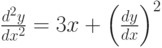 задана краевая задача
задана краевая задача  ;
;  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1,625. чему равно
равна 1,625. чему равно  . В ответе приведите один знак после запятой. Шаг решения методом Эйлера 0,1.
. В ответе приведите один знак после запятой. Шаг решения методом Эйлера 0,1.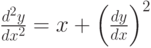 задана краевая задача
задана краевая задача  ;
;  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1,5625. чему равно
равна 1,5625. чему равно  . В ответе приведите один знак после запятой. Шаг решения методом Эйлера 0,1.
. В ответе приведите один знак после запятой. Шаг решения методом Эйлера 0,1.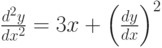 задана краевая задача
задана краевая задача  ;
;  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1,6125. чему равно
равна 1,6125. чему равно  . В ответе приведите один знак после запятой. Шаг решения методом Эйлера 0,1.
. В ответе приведите один знак после запятой. Шаг решения методом Эйлера 0,1. . Начальные условия
. Начальные условия  . Шаг 0,1. В ответе указать значение
. Шаг 0,1. В ответе указать значение  . (Округлить до 4-х знаков после запятой.)
. (Округлить до 4-х знаков после запятой.) . Начальные условия
. Начальные условия  . Шаг 0,05. В ответе указать значение
. Шаг 0,05. В ответе указать значение  . (Округлить до 4-х знаков после запятой.)
. (Округлить до 4-х знаков после запятой.)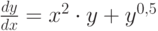 . Начальные условия
. Начальные условия  . Шаг 0,1. В ответе указать значение
. Шаг 0,1. В ответе указать значение  . (Округлить до 4-х знаков после запятой.)
. (Округлить до 4-х знаков после запятой.) . Начальные условия
. Начальные условия  . Шаг 0,15. В ответе указать значение
. Шаг 0,15. В ответе указать значение  . (Округлить до 3-х знаков после запятой.)
. (Округлить до 3-х знаков после запятой.)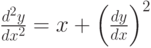 задана краевая задача
задана краевая задача  ;
;  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1,625. чему равно
равна 1,625. чему равно  . В ответе приведите один знак после запятой. Шаг решения методом Эйлера 0,1.
. В ответе приведите один знак после запятой. Шаг решения методом Эйлера 0,1.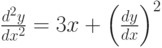 задана краевая задача
задана краевая задача  ;
;  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1. чему равно
равна 1. чему равно  . В ответе приведите один знак после запятой. Шаг решения методом Эйлера 0,1.
. В ответе приведите один знак после запятой. Шаг решения методом Эйлера 0,1.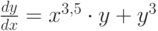 . Начальные условия
. Начальные условия  . Шаг 0,01. В ответе указать значение
. Шаг 0,01. В ответе указать значение  . (Округлить до 4-х знаков после запятой.)
. (Округлить до 4-х знаков после запятой.) . Начальные условия
. Начальные условия  . Шаг 0,05. В ответе указать значение
. Шаг 0,05. В ответе указать значение  . (Округлить до 3-х знаков после запятой.)
. (Округлить до 3-х знаков после запятой.)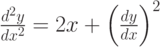 задана краевая задача
задана краевая задача  ;
;  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1,59375. чему равно
равна 1,59375. чему равно  . В ответе приведите один знак после запятой. Шаг решения методом Эйлера 0,1.
. В ответе приведите один знак после запятой. Шаг решения методом Эйлера 0,1. . Начальные условия
. Начальные условия  . Шаг 0,01. В ответе указать значение
. Шаг 0,01. В ответе указать значение  . (Округлить до 4-х знаков после запятой.)
. (Округлить до 4-х знаков после запятой.)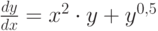 . Начальные условия
. Начальные условия  . Шаг 0,05. В ответе указать значение
. Шаг 0,05. В ответе указать значение  . (Округлить до 4-х знаков после запятой.)
. (Округлить до 4-х знаков после запятой.) . Начальные условия
. Начальные условия  . Шаг 0,15. В ответе указать значение
. Шаг 0,15. В ответе указать значение  . (Округлить до 4-х знаков после запятой.)
. (Округлить до 4-х знаков после запятой.)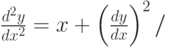 задана краевая задача
задана краевая задача  ;
;  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1,5. чему равно
равна 1,5. чему равно  . В ответе приведите один знак после запятой. Шаг решения методом Эйлера 0,1.
. В ответе приведите один знак после запятой. Шаг решения методом Эйлера 0,1.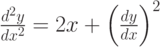 задана краевая задача
задана краевая задача  ;
;  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1,75. чему равно
равна 1,75. чему равно  . В ответе приведите один знак после запятой. Шаг решения методом Эйлера 0,1.
. В ответе приведите один знак после запятой. Шаг решения методом Эйлера 0,1. . Начальные условия
. Начальные условия  . Шаг 0,15. В ответе указать значение
. Шаг 0,15. В ответе указать значение  . (Округлить до 4-х знаков после запятой.)
. (Округлить до 4-х знаков после запятой.)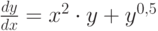 . Начальные условия
. Начальные условия  . Шаг 0,1. В ответе указать значение
. Шаг 0,1. В ответе указать значение  . (Округлить до 4-х знаков после запятой.)
. (Округлить до 4-х знаков после запятой.)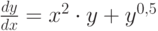 . Начальные условия
. Начальные условия  . Шаг 0,05. В ответе указать значение
. Шаг 0,05. В ответе указать значение  . (Округлить до 3-х знаков после запятой.)
. (Округлить до 3-х знаков после запятой.) . Начальные условия
. Начальные условия  . Шаг 0,01. В ответе указать значение
. Шаг 0,01. В ответе указать значение  . (Округлить до 3-х знаков после запятой.)
. (Округлить до 3-х знаков после запятой.)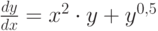 . Начальные условия
. Начальные условия  . Шаг 0,05. В ответе указать значение
. Шаг 0,05. В ответе указать значение  .
. 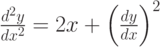 задана краевая задача
задана краевая задача  ;
;  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1,5625. чему равно
равна 1,5625. чему равно  . В ответе приведите один знак после запятой. Шаг решения методом Эйлера 0,1.
. В ответе приведите один знак после запятой. Шаг решения методом Эйлера 0,1.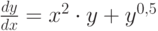 . Начальные условия
. Начальные условия  . Шаг 0,1. В ответе указать значение
. Шаг 0,1. В ответе указать значение  . (Округлить до 3-х знаков после запятой.)
. (Округлить до 3-х знаков после запятой.)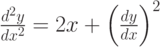 задана краевая задача
задана краевая задача  ;
;  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1,6. чему равно
равна 1,6. чему равно  . В ответе приведите один знак после запятой. Шаг решения методом Эйлера 0,1.
. В ответе приведите один знак после запятой. Шаг решения методом Эйлера 0,1.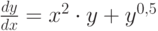 . Начальные условия
. Начальные условия  . Шаг 0,01. В ответе указать значение
. Шаг 0,01. В ответе указать значение  . (Округлить до 4-х знаков после запятой.)
. (Округлить до 4-х знаков после запятой.)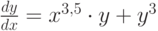 . Начальные условия
. Начальные условия  . Шаг 0,15. В ответе указать значение
. Шаг 0,15. В ответе указать значение  . (Округлить до 3-х знаков после запятой.)
. (Округлить до 3-х знаков после запятой.)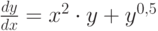 . Начальные условия
. Начальные условия  . Шаг 0,15. В ответе указать значение
. Шаг 0,15. В ответе указать значение  . (Округлить до 3-х знаков после запятой.)
. (Округлить до 3-х знаков после запятой.)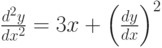 задана краевая задача
задана краевая задача  ;
;  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 2. чему равно
равна 2. чему равно  . В ответе приведите один знак после запятой. Шаг решения методом Эйлера 0,1.
. В ответе приведите один знак после запятой. Шаг решения методом Эйлера 0,1. . Начальные условия
. Начальные условия  . Шаг 0,01. В ответе указать значение
. Шаг 0,01. В ответе указать значение  . (Округлить до 3-х знаков после запятой.)
. (Округлить до 3-х знаков после запятой.)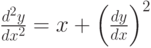 задана краевая задача
задана краевая задача  ;
;  . В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:
. В процессе решения краевой задачи методом стрельб были приняты следующие начальные условия:  ; производная в точке
; производная в точке  равна 1,6. чему равно
равна 1,6. чему равно  . В ответе приведите один знак после запятой. Шаг решения методом Эйлера 0,1.
. В ответе приведите один знак после запятой. Шаг решения методом Эйлера 0,1.