Не меньше какого числа должно быть  , чтобы выполнялось следующая теорема? Пусть
, чтобы выполнялось следующая теорема? Пусть 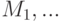
 -элементные подмножества какого-то множества, причем каждый элемент этого множества принадлежит не более чем
-элементные подмножества какого-то множества, причем каждый элемент этого множества принадлежит не более чем  множествам
множествам 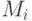 , тогда существует одноцветная раскраска данного
, тогда существует одноцветная раскраска данного  -элементного подмножества.
-элементного подмножества.
(Ответ необходимо ввести в поле ввода.)
Варианты ответа

 .Пусть
.Пусть  ?
? состоит в том, что
состоит в том, что  ,
,  ,...,
,..., ,...,
,...,  . Обозначим
. Обозначим  . Рассмотрим
. Рассмотрим  - совокупность независимых множеств вершин Кнезеровского графа
- совокупность независимых множеств вершин Кнезеровского графа  . Допустим,
. Допустим, 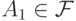 . Выберите все множества, которые в таком случае также попадают в
. Выберите все множества, которые в таком случае также попадают в 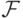 кроме
кроме  ?
?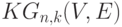 построенный следующим образом? Имеется
построенный следующим образом? Имеется 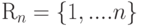 - множество натуральных чисел от 1 до
- множество натуральных чисел от 1 до  -элементные подмножества из множества
-элементные подмножества из множества 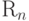 . Говорят, что пара
. Говорят, что пара  образуют ребро графа, тогда и только тогда
образуют ребро графа, тогда и только тогда  .
.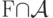 ?
?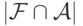 ?
?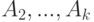 и
и  выберите множество, с котором не пересекается
выберите множество, с котором не пересекается 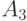 .
.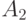 .
.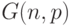 -случайный граф, множество, состоящее из
-случайный граф, множество, состоящее из  , которая независит от вероятности проведения других ребер и может зависеть от
, которая независит от вероятности проведения других ребер и может зависеть от 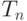 - число треугольников в случайном графе. Если
- число треугольников в случайном графе. Если 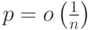 , то к чему ассимтотические стремится математическое ожидание
, то к чему ассимтотические стремится математическое ожидание  ?
?