Дискретный анализ и теория вероятностей

Сколько решений имеет характеристическое уравнение для рекуррентного соотношения $y_{n+2}+2y_{n+1}+y_{n}=0$ ?

(Ответ необходимо ввести в поле ввода.)

Варианты ответа

Похожие вопросы

Найдите наибольшее по модулю решение характеристическое уравнение для рекуррентного соотношения $y_{n+2}+2y_{n+1}-3y_{n}=0$ .

Найдите наибольшее по модулю решение характеристическое уравнение для рекуррентного соотношения $y_{n+2}-2y_{n+1}+3y_{n}=0$

Найдите наименьшее по модулю решение характеристическое уравнение для рекуррентного соотношения $y_{n+2}+2y_{n+1}-3y_{n}=0$ .

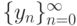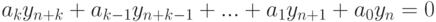Как выглядит характеристическое уравнение для cоотношения на элементы бесконечной последовательности $\{y_n\}^\infty_{n=0}$ удовлетворяющее условию $a_k y_{n+k}+a_{k-1} y_{n+k-1}+...+a_1 y_{n+1}+a_0 y_{n}=0$ , где постоянные величины $a_0,...,a_k \in C$ , если k=2

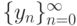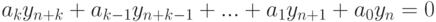Сколько решений имеет cоотношение на элементы бесконечной последовательности $\{y_n\}^\infty_{n=0}$ удовлетворяющее условию $a_k y_{n+k}+a_{k-1} y_{n+k-1}+...+a_1 y_{n+1}+a_0 y_{n}=0$ , где постоянные величины $a_0,...,a_k \in C$ ?

Имеется множество натуральных чисел от 1 до

. И определены следуюшие подмножества $A_1=\{1,2,...,k\}$ , $A_2=\{2,3,...,k+1\}$ ,..., $A_{n-k-1}=\{n-k-1,...,n\}$ ,..., $A_{n}=\{n,1,...,k-1\}$ . Обозначим ${\cal A }=\{ A_1,...,A_n \}$ . Рассмотрим ${\cal F }=\{ F_1,...,F_s \}$ - совокупность независимых множеств вершин Кнезеровского графа KG(n,k)

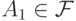. Допустим, $A_1 \in {\cal F}$ . Выберите все множества, которые в таком случае также попадают в 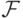${\cal F}$ кроме A_1

Имеется множество натуральных чисел от 1 до

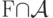. Что является наиболее точной верхней оценкой мощности ${\cal F}\cap{\cal A}$ ?

Имеется множество натуральных чисел от 1 до

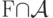. Что верно относительно мощности ${\cal F}\cap{\cal A}$ ?

Имеется множество натуральных чисел от 1 до

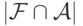. Что верно относительно $| {\cal F}\cap{\cal A}|$ ?

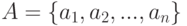Имеется множество $A=\left \{a_1,a_2,...,a_n\right\}$ и множество

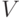– все размещения с повторениями из элементов множества по

по

. Известно, что m<n

. Рассмотрим свойство $\alpha_i,i=1,...,n$ которым или обладает или не обладает каждый элемент из множества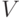

. Размещение обладает свойством $\alpha_i,i=1,...,n$ , если элемент a_i

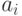не принадлежит данному размещению. Сколько

размещений не обладает ни одним из свойств $\alpha_i,i=1,...,n$ ?

Дискретный анализ и теория вероятностей

Сколько решений имеет характеристическое уравнение для рекуррентного соотношения ?

Сколько решений имеет характеристическое уравнение для рекуррентного соотношения $y_{n+2}+2y_{n+1}+y_{n}=0$ ?