Выберите выражение равное 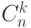 .
.
(Отметьте один правильный вариант ответа.)
Варианты ответа

 (Верный ответ)
(Верный ответ)

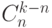

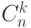 .
.
 (Верный ответ)
(Верный ответ)

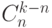
 вершинами и циклом, построенным на
вершинами и циклом, построенным на  вершинах
вершинах 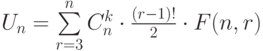 выражение
выражение 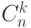 показывает...
показывает... . И определены следуюшие подмножества
. И определены следуюшие подмножества  ,
,  ,...,
,..., ,...,
,...,  . Обозначим
. Обозначим  . Рассмотрим
. Рассмотрим  - совокупность независимых множеств вершин Кнезеровского графа
- совокупность независимых множеств вершин Кнезеровского графа  . Допустим,
. Допустим, 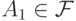 . Выберите все множества, которые в таком случае также попадают в
. Выберите все множества, которые в таком случае также попадают в 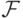 кроме
кроме  ?
? . И определены следуюшие подмножества
. И определены следуюшие подмножества  ,
,  ,...,
,..., ,...,
,...,  . Обозначим
. Обозначим  .Среди множеств
.Среди множеств 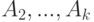 и
и  выберите множество, с котором не пересекается
выберите множество, с котором не пересекается 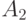 .
. . И определены следуюшие подмножества
. И определены следуюшие подмножества  ,
,  ,...,
,..., ,...,
,...,  . Обозначим
. Обозначим  .Среди множеств
.Среди множеств 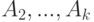 и
и  выберите множество, с котором не пересекается
выберите множество, с котором не пересекается 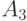 .
. . И определены следуюшие подмножества
. И определены следуюшие подмножества  ,
,  ,...,
,..., ,...,
,...,  . Обозначим
. Обозначим  . Рассмотрим
. Рассмотрим  - совокупность независимых множеств вершин Кнезеровского графа
- совокупность независимых множеств вершин Кнезеровского графа  . Что является наиболее точной верхней оценкой мощности
. Что является наиболее точной верхней оценкой мощности 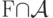 ?
? . И определены следуюшие подмножества
. И определены следуюшие подмножества  ,
,  ,...,
,..., ,...,
,...,  . Обозначим
. Обозначим  . Рассмотрим
. Рассмотрим  - совокупность независимых множеств вершин Кнезеровского графа
- совокупность независимых множеств вершин Кнезеровского графа  . Что верно относительно мощности
. Что верно относительно мощности 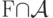 ?
? на
на  вершинах в красный и синий цвета. Пусть
вершинах в красный и синий цвета. Пусть  -вероятность покрасить ребро в красный цвет и
-вероятность покрасить ребро в красный цвет и  - вероятность покрасить ребро в синий цвет. Определим события
- вероятность покрасить ребро в синий цвет. Определим события 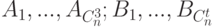 , где
, где  -состоит в том, что
-состоит в том, что  -ый треугольник целиком красный и
-ый треугольник целиком красный и 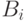 -состоит в том, что
-состоит в том, что  -ая клика размера
-ая клика размера  целиком синяя. Если для некоторого события
целиком синяя. Если для некоторого события  построен орграф зависимостей, то какое выражение позволит сверху оценить количество ребер, которые выйдут из вершины
построен орграф зависимостей, то какое выражение позволит сверху оценить количество ребер, которые выйдут из вершины  орграфа зависимостей в вершины
орграфа зависимостей в вершины 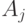 ?
?