Чему равно ![C_n^{\left[ an \right]}](https://intuit.ru//sites/default/files/tex_cache/2d98e22dfffb7ba9671b70b5fe395420.png) , где
, где  ?
?
(Отметьте один правильный вариант ответа.)
Варианты ответа
 (Верный ответ)
(Верный ответ)
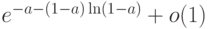


![C_n^{\left[ an \right]}](https://intuit.ru//sites/default/files/tex_cache/2d98e22dfffb7ba9671b70b5fe395420.png) , где
, где  ?
? (Верный ответ)
(Верный ответ)
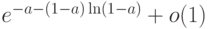

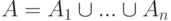 . Введем на подмножествах множества индексов
. Введем на подмножествах множества индексов  функцию
функцию 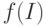 , где
, где 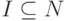 . Пусть
. Пусть 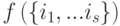 обозначает число элементов множества
обозначает число элементов множества  , которые могут не принадлежать каким-то из подмножеств
, которые могут не принадлежать каким-то из подмножеств 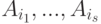 , но обязаны принадлежать каждому из остальных подмножеств. Чему равно
, но обязаны принадлежать каждому из остальных подмножеств. Чему равно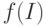 при
при 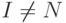 ?
?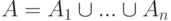 . Введем на подмножествах множества индексов
. Введем на подмножествах множества индексов  функцию
функцию 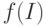 , где
, где 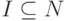 . Пусть
. Пусть 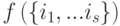 обозначает число элементов множества
обозначает число элементов множества  , которые могут не принадлежать каким-то из подмножеств
, которые могут не принадлежать каким-то из подмножеств 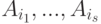 , но обязаны принадлежать каждому из остальных подмножеств. Чему равно
, но обязаны принадлежать каждому из остальных подмножеств. Чему равно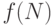 ?
? . И определены следуюшие подмножества
. И определены следуюшие подмножества  ,
,  ,...,
,..., ,...,
,...,  . Обозначим
. Обозначим  . Рассмотрим
. Рассмотрим  - совокупность независимых множеств вершин Кнезеровского графа
- совокупность независимых множеств вершин Кнезеровского графа  . Допустим,
. Допустим, 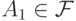 . Выберите все множества, которые в таком случае также попадают в
. Выберите все множества, которые в таком случае также попадают в 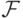 кроме
кроме  ?
?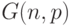 -случайный граф, множество, состоящее из
-случайный граф, множество, состоящее из  вершин, а каждое ребро проводим с вероятностью
вершин, а каждое ребро проводим с вероятностью  , которая независит от вероятности проведения других ребер и может зависеть от
, которая независит от вероятности проведения других ребер и может зависеть от  . Пусть случайная величина
. Пусть случайная величина 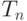 - число треугольников в случайном графе. Если
- число треугольников в случайном графе. Если 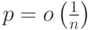 , то к чему ассимтотические стремится математическое ожидание
, то к чему ассимтотические стремится математическое ожидание  ?
? . И определены следуюшие подмножества
. И определены следуюшие подмножества  ,
,  ,...,
,..., ,...,
,...,  . Обозначим
. Обозначим  . Рассмотрим
. Рассмотрим  - совокупность независимых множеств вершин Кнезеровского графа
- совокупность независимых множеств вершин Кнезеровского графа  . Что является наиболее точной верхней оценкой мощности
. Что является наиболее точной верхней оценкой мощности 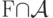 ?
? в два цвета - красный и синий. Пусть событие
в два цвета - красный и синий. Пусть событие 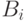 состоит в том, что в случайной раскраске
состоит в том, что в случайной раскраске  -ая по счету клика
-ая по счету клика 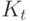 в графе
в графе  целиком синяя. Чему равно
целиком синяя. Чему равно 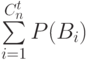 ?
? в два цвета - красный и синий. Пусть событие
в два цвета - красный и синий. Пусть событие  состоит в том, что в случайной раскраске
состоит в том, что в случайной раскраске  -ая по счету клика
-ая по счету клика  в графе
в графе  целиком красная. Чему равно
целиком красная. Чему равно  ?
?