Сколько требуется знать начальных условий, чтобы однозначно определить решение для cоотношения на элементы бесконечной последовательности 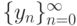 удовлетворяющее условию
удовлетворяющее условию 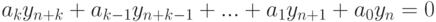 , где постоянные величины
, где постоянные величины  ?
?
(Отметьте один правильный вариант ответа.)
Варианты ответа
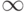

 (Верный ответ)
(Верный ответ)
0

 ?
? ,
,  ,...,
,..., ,...,
,...,  . Обозначим
. Обозначим  . Рассмотрим
. Рассмотрим  - совокупность независимых множеств вершин Кнезеровского графа
- совокупность независимых множеств вершин Кнезеровского графа  . Допустим,
. Допустим, 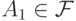 . Выберите все множества, которые в таком случае также попадают в
. Выберите все множества, которые в таком случае также попадают в 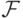 кроме
кроме  ?
?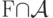 ?
?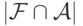 ?
? . Из множества
. Из множества  выбираем случайные подмножества
выбираем случайные подмножества  и
и  из
из  , по схеме выбора с возращением
, по схеме выбора с возращением 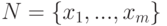 . Пусть определены события
. Пусть определены события 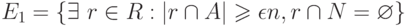 и
и  . Какое
. Какое 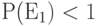 ?
?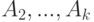 и
и  выберите множество, с котором не пересекается
выберите множество, с котором не пересекается 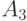 .
.