Чему согласно теореме Муавра-Лапласа равна вероятность того, что число успехов по схеме Бернулли, центрированное 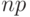 и нормированное
и нормированное  находится в пределах от
находится в пределах от  до
до  , если
, если  - число испытаний,
- число испытаний,  - вероятность успеха в одном испытании,
- вероятность успеха в одном испытании, 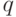 - вероятность неудачи в одном испытании?
- вероятность неудачи в одном испытании?
(Отметьте один правильный вариант ответа.)
Варианты ответа
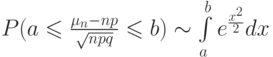
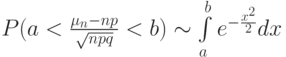
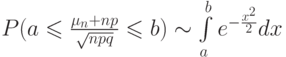
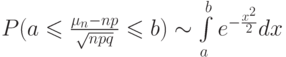 (Верный ответ)
(Верный ответ)

 , если
, если 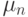 -число успехов в
-число успехов в  вероятность ровно
вероятность ровно  успехов в
успехов в 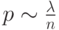 , где постоянная
, где постоянная  ?
? ,
,  ,...,
,..., ,...,
,...,  . Обозначим
. Обозначим  . Рассмотрим
. Рассмотрим  - совокупность независимых множеств вершин Кнезеровского графа
- совокупность независимых множеств вершин Кнезеровского графа  . Допустим,
. Допустим, 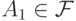 . Выберите все множества, которые в таком случае также попадают в
. Выберите все множества, которые в таком случае также попадают в 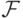 кроме
кроме  ?
? на
на  - вероятность покрасить ребро в синий цвет. Определим события
- вероятность покрасить ребро в синий цвет. Определим события 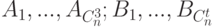 , где
, где  -состоит в том, что
-состоит в том, что  -ый треугольник целиком красный и
-ый треугольник целиком красный и 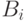 -состоит в том, что
-состоит в том, что  целиком синяя. Чему равна
целиком синяя. Чему равна  ?
?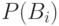 ?
?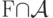 ?
?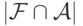 ?
?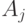 ?
? .Пусть
.Пусть 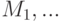
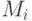 , тогда существует одноцветная раскраска данного
, тогда существует одноцветная раскраска данного