Функция  называется невозрастающей на [a,b], если
называется невозрастающей на [a,b], если ![\forall x_1, x_2 \in [a,b]: x_1 < x_2](https://intuit.ru//sites/default/files/tex_cache/e210b3b7e225b2ed9c466bd4af6172d3.png)
(Отметьте один правильный вариант ответа.)
Варианты ответа
 (Верный ответ)
(Верный ответ)
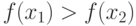



 называется невозрастающей на [a,b], если
называется невозрастающей на [a,b], если ![\forall x_1, x_2 \in [a,b]: x_1 < x_2](https://intuit.ru//sites/default/files/tex_cache/e210b3b7e225b2ed9c466bd4af6172d3.png)
 (Верный ответ)
(Верный ответ)
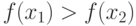


 - критическая точка
- критическая точка  , но
, но  непрерывна в
непрерывна в  . Тогда функция
. Тогда функция  в точке
в точке  имеет экстремум, если её производная
имеет экстремум, если её производная  при переходе через точку
при переходе через точку 
 - критическая точка
- критическая точка  , но
, но  непрерывна в
непрерывна в  . Тогда функция
. Тогда функция  в точке
в точке  имеет максимум, если её производная
имеет максимум, если её производная  при переходе через точку
при переходе через точку 
 - критическая точка
- критическая точка  , но
, но  непрерывна в
непрерывна в  . Тогда функция
. Тогда функция  в точке
в точке  имеет минимум, если её производная
имеет минимум, если её производная  при переходе через точку
при переходе через точку 
 в окрестности точки
в окрестности точки  существует производная
существует производная  -го порядка, непрерывная в
-го порядка, непрерывная в  и
и 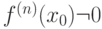 - первая отличная от нуля производная. Тогда
- первая отличная от нуля производная. Тогда  - точка максимума
- точка максимума  , если
, если в окрестности точки
в окрестности точки  существует производная
существует производная  -го порядка и
-го порядка и 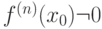 - первая отличная от нуля производная. Тогда
- первая отличная от нуля производная. Тогда  - не является точкой минимума и максимума
- не является точкой минимума и максимума  , если
, если в окрестности точки
в окрестности точки  существует производная
существует производная  -го порядка и
-го порядка и 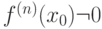 - первая отличная от нуля производная. Тогда
- первая отличная от нуля производная. Тогда  - точка минимума
- точка минимума  , если
, если