Дифференциальное исчисление функций одной переменной - ответы
Количество вопросов - 259
Какая их формул является разложением Маклорена для функции 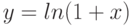 c остаточным членом в форме Пеано:
c остаточным членом в форме Пеано:
Для каких функций точка 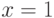 является критической точкой:
является критической точкой:
Прямая  является горизонтальной асимптотой графика функции
является горизонтальной асимптотой графика функции  , если
, если
Пусть выполнены условия теоремы 5 (правило Лопиталя) для бесконечно больших функций  и
и  . Тогда предел
. Тогда предел 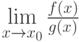
Функция  называется дифференцируемой в точке
называется дифференцируемой в точке  , если приращение
, если приращение  можно представить в виде (
можно представить в виде ( )
)
Пусть функция  в точке
в точке 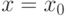 имеет производную
имеет производную 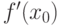 . Какое утверждение верно:
. Какое утверждение верно:
Если  , то прямая
, то прямая 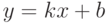
Функция  может иметь экстремум только в тех точках, в которых её производная
может иметь экстремум только в тех точках, в которых её производная 
Пусть функция  непрерывна на [a,b] и имеет производную
непрерывна на [a,b] и имеет производную  на интервале (a,b). Какое утверждение верно:
на интервале (a,b). Какое утверждение верно:
Для функции 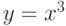 точка (0,0) графика функции является
точка (0,0) графика функции является
Для каких функций точка перегиба имеет абсциссу 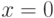 :
:
Пусть точка  - точка разрыва функции
- точка разрыва функции  и прямая
и прямая 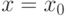 - вертикальная асимптота. Тогда
- вертикальная асимптота. Тогда  -
-
Указать интервалы монотонности функции 
Какие числа могут быть точками 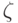 из теоремы Ролля для функции
из теоремы Ролля для функции 
Производной вектор-функции  по её аргументу
по её аргументу  называется
называется
Проверить выполнение условий теоремы 6 для применения правила Лопиталя при вычислении предела 
Если прямая 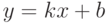 является наклонной асимптотой графика функции
является наклонной асимптотой графика функции  , то
, то
Функция  называется невозрастающей на [a,b], если
называется невозрастающей на [a,b], если ![\forall x_1, x_2 \in [a,b]: x_1 < x_2](https://intuit.ru//sites/default/files/tex_cache/e210b3b7e225b2ed9c466bd4af6172d3.png)
Производная функции 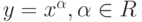 равна
равна
Производной функции  в данной точке
в данной точке  называется
называется
Какая из формул является выражением для остаточного члена 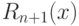 в форме Пеано:
в форме Пеано:
Производная функции 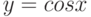 равна
равна
Какие утверждения справедливы:
Какие условия для функции  должны выполняться, чтобы её можно было разложить в ряд Тейлора в окрестности точки
должны выполняться, чтобы её можно было разложить в ряд Тейлора в окрестности точки  :
:
Какому условию должны удовлетворять функции  , чтобы их произведение
, чтобы их произведение  было дифференцируемым:
было дифференцируемым:
График дифференцируемой на интервале  функции
функции  не имеет на этом интервале выпуклость, направленную вверх или вниз, если график
не имеет на этом интервале выпуклость, направленную вверх или вниз, если график  лежит в пределах интервала
лежит в пределах интервала
В условиях теоремы Лагранжа точка 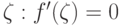
Второе приближение 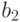 корня уравнения
корня уравнения  на отрезке
на отрезке ![[a,b]](https://intuit.ru//sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) методом касательных вычисляется по формуле:
методом касательных вычисляется по формуле:
Производная функции 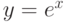 равна
равна
Чему равна производная функции 
Производной функции является функция
является функция
Угловой коэффициент касательной, проведённой к кривой  в точке с абсциссой
в точке с абсциссой  , равен
, равен
Левой производной 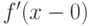 функции
функции  в данной точке
в данной точке  называется
называется
Какие из функций имеют равные правые и левые производные в точке  :
:
Если касательная, проведённая к кривой  в точке
в точке 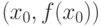 , параллельна оси Oy, то
, параллельна оси Oy, то 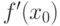
Для каких из перечисленных функций  :
:
Какое условие эквивалентно дифференцируемости функции  в точке
в точке  :
:
Какие из перечисленных функций дифференцируемы в точке 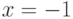 :
:
Производная функции  равна
равна
Какому условию должны удовлетворять функции 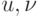 , чтобы их сумма
, чтобы их сумма 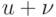 была дифференцируемой:
была дифференцируемой:
Для какого числа множеств выполняются правила дифференцирования их суммы:
Производная показательной функции 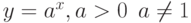 равна
равна
Производная функции 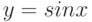 равна
равна
Чему равна производная сложной функции ![y = f[\varphi (x)]](https://intuit.ru//sites/default/files/tex_cache/ead719ea19850ef1759fce07ef02772d.png) в точке
в точке 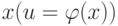 :
:
Чему равна производная функции 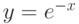
Какая из перечисленных функций является обратной для функции 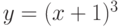
Пусть функция 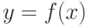 непрерывна и убывает на
непрерывна и убывает на![[a,b]](https://intuit.ru//sites/default/files/tex_cache/3f25293cb3f7d82aca4fcb642825f054.png) . Тогда обратная функция
. Тогда обратная функция  :
:
Пусть функции  и
и  взаимно обратные. Отметьте верные утверждения:
взаимно обратные. Отметьте верные утверждения:
Пусть задана функция  . Отметьте верные утверждения:
. Отметьте верные утверждения:
Производная функции 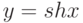 равна
равна
Производная функции 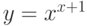 с помощью логарифмического дифференцирования вычисляется по формуле:
с помощью логарифмического дифференцирования вычисляется по формуле:
Приближённое значение функции 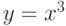 в точке
в точке 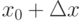 равно
равно
Производная  -го порядка
-го порядка 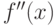 функции
функции 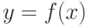 есть
есть
Может ли существовать вторая производная  в точке
в точке  , если в неё не существует первая производная
, если в неё не существует первая производная 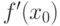 :
:
Чему равна  -я производная функции
-я производная функции 
Производная  -го порядка
-го порядка 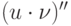 произведения двух функций
произведения двух функций  равна
равна
Дифференциал  -го порядка
-го порядка 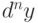 функции
функции  можно вычислить по формуле
можно вычислить по формуле
Пусть функция  задана параметрически:
задана параметрически: 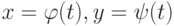 . Каким условиям должна удовлетворять функция
. Каким условиям должна удовлетворять функция 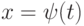 на интервале
на интервале 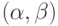 для того, чтобы существовала производная
для того, чтобы существовала производная 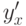 :
:
Постоянный вектор  называется пределом вектор-функции
называется пределом вектор-функции  при
при 
Чему равна производная вектор-функции 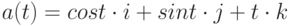
Каким условиям должна удовлетворять функция  в теореме Ролля:
в теореме Ролля:
В условиях теоремы Коши точка 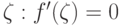
В условиях теоремы Коши точка 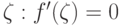
Какое условие теоремы Ролля не выполняется для функции ![f(x) = x - [x] \, 0 \leq x \leq 1](https://intuit.ru//sites/default/files/tex_cache/2d29703fbb5b42336d45261071a805ae.png) :
:
Геометрический смысл теоремы Лагранжа состоит в том, что существует хотя бы одна точка графика функции  , в которой касательная
, в которой касательная
Какое выражение является формулой Лагранжа для функции  на отрезке [a,b]:
на отрезке [a,b]:
Какой должна быть функция 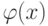 , чтобы теорема Лагранжа стала следствием теоремы Коши:
, чтобы теорема Лагранжа стала следствием теоремы Коши:
Какую неопределённость нужно раскрыть при вычислении предела функции 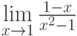 :
:
Пусть  и
и  - бесконечно большие на бесконечности функции, для которых существует предел
- бесконечно большие на бесконечности функции, для которых существует предел 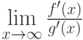 . Тогда существует предел
. Тогда существует предел
Каким условиям на бесконечности должны удовлетворять функции  и
и  , чтобы выполнялось правило Лопиталя:
, чтобы выполнялось правило Лопиталя:
Пусть выполнены условия теоремы 4 (правило Лопиталя) для бесконечно малых функций  и
и  . Тогда предел
. Тогда предел 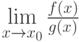
Какие утверждения справедливы:
Какое выражение является формулой Маклорена для многочлена степени  :
:
Верно ли, что  раз дифференцируемую в окрестности точки
раз дифференцируемую в окрестности точки  функцию
функцию  можно представить в виде формулыТейлора?
можно представить в виде формулыТейлора?
Верно ли, что функция 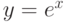 раскладывается в ряд Маклорена в любой окрестности точки
раскладывается в ряд Маклорена в любой окрестности точки 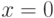
Какое выражение является многочленом Тейлора  для
для  раз дифференцируемой в окрестности точки
раз дифференцируемой в окрестности точки 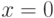 функции
функции 
Какая их формул является разложением Маклорена для функции 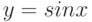 c остаточным членом в форме Пеано:
c остаточным членом в форме Пеано:
Функция  называется неубывающей на [a,b], если
называется неубывающей на [a,b], если ![\forall x_1, x_2 \in [a,b]: x_1 < x_2](https://intuit.ru//sites/default/files/tex_cache/e210b3b7e225b2ed9c466bd4af6172d3.png)
Пусть функция  непрерывна на [a,b] и имеет производную
непрерывна на [a,b] и имеет производную  на интервале (a,b). Какое утверждение верно:
на интервале (a,b). Какое утверждение верно:
Пусть функция  непрерывна на [a,b] и имеет производную
непрерывна на [a,b] и имеет производную  на интервале (a,b). Какое утверждение верно:
на интервале (a,b). Какое утверждение верно:
Указать интервалы монотонности функции 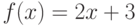
Точка  не является точкой локального минимума функции
не является точкой локального минимума функции  , если
, если
Для каких функций точка 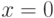 является точкой локального максимума:
является точкой локального максимума:
Какие из утверждений справедливы:
Пусть  - критическая точка
- критическая точка  , но
, но  непрерывна в
непрерывна в  . Тогда функция
. Тогда функция  в точке
в точке  имеет максимум, если её производная
имеет максимум, если её производная  при переходе через точку
при переходе через точку 
Пусть в точке  функция
функция  имеет первую и вторую производные. Какие условия являются достаточными, чтобы точка
имеет первую и вторую производные. Какие условия являются достаточными, чтобы точка  была точкой максимума для
была точкой максимума для  :
:
Наименьшее значение функция  может принимать
может принимать
Выпуклость кривой  в точке
в точке 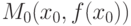 направлена вверх, если
направлена вверх, если
Точка 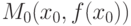 является точкой перегиба кривой
является точкой перегиба кривой  , если в этой точке
, если в этой точке
Какие условия являются достаточными, чтобы точка 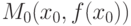 была точкой перегиба кривой
была точкой перегиба кривой 
Прямая 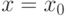 является вертикальной асимптотой графика функции
является вертикальной асимптотой графика функции  только в том случае, если
только в том случае, если
Пусть прямая 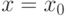 - вертикальная асимптота функции
- вертикальная асимптота функции  . Тогда точка
. Тогда точка  может быть
может быть
Для каких функций прямая 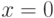 является вертикальной асимптотой:
является вертикальной асимптотой:
Если прямая 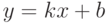 является наклонной асимптотой графика функции
является наклонной асимптотой графика функции  , то
, то  равно
равно
Если прямая 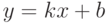 является наклонной асимптотой графика функции
является наклонной асимптотой графика функции  , то
, то  равно
равно
Прямая 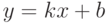 является наклонной асимптотой графика функции
является наклонной асимптотой графика функции  , если
, если
Если 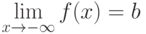 , то прямая
, то прямая 
Для функции 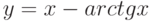 наклонные асимптоты при
наклонные асимптоты при 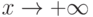 и
и 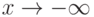
Пусть для функции  в окрестности точки
в окрестности точки  существует производная
существует производная  -го порядка и
-го порядка и 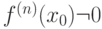 - первая отличная от нуля производная. Тогда
- первая отличная от нуля производная. Тогда 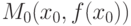 является точкой перегиба графика функции, если
является точкой перегиба графика функции, если
Из предложенного списка выбрать те условия, которым должна удовлетворять функция  , чтобы уравнение
, чтобы уравнение  на отрезке
на отрезке ![[a,b]](https://intuit.ru//sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) имело единственное решение:
имело единственное решение:
Какое условие должно выполняться в точке  , чтобы при применении метода хорд точка пересечения хорды с осью
, чтобы при применении метода хорд точка пересечения хорды с осью  было приближением к корню уравнения
было приближением к корню уравнения  на отрезке
на отрезке ![[a,b]](https://intuit.ru//sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) :
:
Последовательности приближений корня уравнения  на отрезке
на отрезке ![[a,b]](https://intuit.ru//sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) методом хорд и касательных являются
методом хорд и касательных являются
Для какого числа функций выполняются правила дифференцирования их произведения:
Какое выражение является формулой Тейлора для многочлена степени  :
:
Производная функции ![y = [u(x)]^{\nu (x)}](https://intuit.ru//sites/default/files/tex_cache/f448859cd75aef92a0b406ee93a88b80.png) с помощью логарифмического дифференцирования вычисляется по
с помощью логарифмического дифференцирования вычисляется по
Из предложенного списка выбрать те условия, которым должна удовлетворять функция  , чтобы уравнение
, чтобы уравнение  на отрезке
на отрезке ![[a,b]](https://intuit.ru//sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) имело хотя бы одно решение:
имело хотя бы одно решение:
Пусть выполнены условия теоремы 6 (правило Лопиталя) для бесконечно больших функций  и
и  на бесконечности. Тогда предел
на бесконечности. Тогда предел 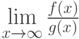
Производная функции  равна
равна
Пусть функция  задана параметрически:
задана параметрически: 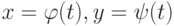 . Чему равна производная
. Чему равна производная 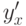 :
:
Точка  не является точкой локального максимума функции
не является точкой локального максимума функции  , если
, если
Дифференциалом 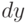 функции
функции  называется
называется
Для каких функций точка 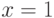 является точкой локального минимума:
является точкой локального минимума:
Указать интервалы монотонности функции 
Чему равна  -я производная функции
-я производная функции 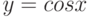
Дифференциалом  -го порядка
-го порядка 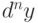 функции
функции  называется
называется
Если в точке  существует производная
существует производная  , то
, то
Какие условия являются достаточными, чтобы точка 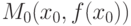 была точкой перегиба кривой
была точкой перегиба кривой 
Пусть функция  в точке
в точке 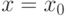 имеет производную
имеет производную 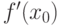 . Какое утверждение верно:
. Какое утверждение верно:
Какое условие должно выполняться в точке  , чтобы при применении метода касательных точка пересечения касательной с осью
, чтобы при применении метода касательных точка пересечения касательной с осью  было приближением к корню уравнения
было приближением к корню уравнения  на отрезке
на отрезке ![[a,b]](https://intuit.ru//sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) :
:
Пусть функции  и
и  взаимно обратные. Отметьте верные утверждения:
взаимно обратные. Отметьте верные утверждения:
Какие условия являются необходимыми, чтобы точка 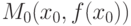 была точкой перегиба кривой
была точкой перегиба кривой 
Верно ли, что функция 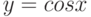 раскладывается в ряд Маклорена в любой окрестности точки
раскладывается в ряд Маклорена в любой окрестности точки 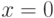
Производная 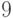 -го порядка
-го порядка 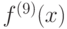 функции
функции 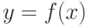 есть
есть
Пусть для функции  в окрестности точки
в окрестности точки  существует производная
существует производная  -го порядка и
-го порядка и 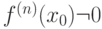 - первая отличная от нуля производная. Тогда
- первая отличная от нуля производная. Тогда  - точка минимума
- точка минимума  , если
, если
Если 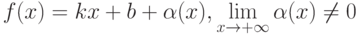 , то прямая
, то прямая 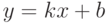
Какие утверждения справедливы:
Какие из перечисленных функций дифференцируемы в точке  :
:
Производная функции 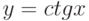 равна
равна
Если  , то прямая
, то прямая 
Каким условиям в точке  должны удовлетворять функции
должны удовлетворять функции  и
и  , чтобы выполнялось правило Лопиталя:
, чтобы выполнялось правило Лопиталя:
Какое из перечисленных уравнений является уравнением касательной к кривой  в точке с абсциссой
в точке с абсциссой  :
:
Какие из функций имеют равные правые и левые производные в точке  :
:
Если функция  в точке
в точке  имеет бесконечную производную
имеет бесконечную производную 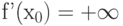 , то касательная, проведённая к кривой
, то касательная, проведённая к кривой  в точке
в точке 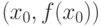
Если функции 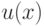 дифференцируема в точке
дифференцируема в точке  и
и 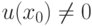 , а
, а 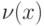 не дифференцируема в точке
не дифференцируема в точке  , то их произведение
, то их произведение  в этой точке
в этой точке
Производная функции  равна
равна
Чему равна производная сложной функции ![y = f[\varphi (x)]](https://intuit.ru//sites/default/files/tex_cache/ead719ea19850ef1759fce07ef02772d.png) в точке
в точке 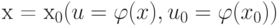 :
:
Функции 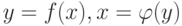 называются взаимно обратными, если
называются взаимно обратными, если
Производная функции 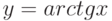 равна
равна
Производная функции 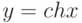 равна
равна
Приближённое значение функции ![y = \sqrt[3]{x}](https://intuit.ru//sites/default/files/tex_cache/e792c08aeb14d2f64b8026bb73f83d37.png) в точке
в точке 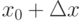 равно
равно
Пусть существует  -я производная
-я производная 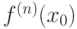 в точке
в точке  . Существует ли производная меньшего порядка
. Существует ли производная меньшего порядка  :
:
Дифференциалом  -го порядка
-го порядка 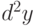 функции
функции  называется
называется
Пусть функция  задана параметрически:
задана параметрически: 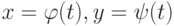 . Каким условиям должна удовлетворять функция
. Каким условиям должна удовлетворять функция 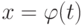 на интервале
на интервале 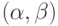 для того, чтобы существовала производная
для того, чтобы существовала производная 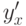 :
:
Постоянный вектор  не является пределом вектор-функции
не является пределом вектор-функции  при
при 
В условиях теоремы Ролля точка 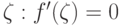
В условиях теоремы Ролля точка 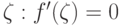
Какое условие теоремы Ролля не выполняется для функции  :
:
Какое выражение является формулой Коши для функций 
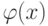 на отрезке [a,b]:
на отрезке [a,b]:
Пусть  и
и  - бесконечно малые в точке
- бесконечно малые в точке  функции, для которых существует предел
функции, для которых существует предел 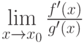 . Тогда существует предел
. Тогда существует предел
Каким свойством обладает многочлен Тейлора  функции
функции 
Какая их формул является разложением Маклорена для функции 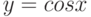 c остаточным членом в форме Пеано:
c остаточным членом в форме Пеано:
Функция  называется возрастающей на [a,b], если
называется возрастающей на [a,b], если ![\forall x_1, x_2 \in [a,b]: x_1 < x_2](https://intuit.ru//sites/default/files/tex_cache/e210b3b7e225b2ed9c466bd4af6172d3.png)
Точка  называется точкой локального максимума функции
называется точкой локального максимума функции  , если
, если
Для каких функций точка 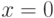 является точкой локального минимума:
является точкой локального минимума:
Для каких функций точка 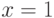 является точкой экстремума:
является точкой экстремума:
Пусть  - критическая точка
- критическая точка  , но
, но  непрерывна в
непрерывна в  . Тогда функция
. Тогда функция  в точке
в точке  имеет минимум, если её производная
имеет минимум, если её производная  при переходе через точку
при переходе через точку 
График дифференцируемой на интервале 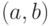 функции
функции  не имеет на этом интервале выпуклость, направленную вверх, если график
не имеет на этом интервале выпуклость, направленную вверх, если график  лежит в пределах интервала
лежит в пределах интервала
Для каких функций точка перегиба имеет абсциссу 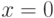 :
:
Если прямая 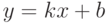 является наклонной асимптотой графика функции
является наклонной асимптотой графика функции  , то
, то
Если прямая 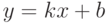 является наклонной асимптотой графика функции
является наклонной асимптотой графика функции  , то
, то  равно
равно
Прямая 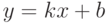 является наклонной асимптотой графика функции
является наклонной асимптотой графика функции  , если
, если
Прямая  является горизонтальной асимптотой графика функции
является горизонтальной асимптотой графика функции  , если
, если
Для функции  наклонные асимптоты при
наклонные асимптоты при 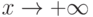 и
и 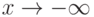
Пусть для функции  в окрестности точки
в окрестности точки  существует производная
существует производная  -го порядка, непрерывная в
-го порядка, непрерывная в  и
и 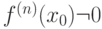 - первая отличная от нуля производная. Тогда
- первая отличная от нуля производная. Тогда  - точка максимума
- точка максимума  , если
, если
Для функции  точка (0,1) графика функции является
точка (0,1) графика функции является
Если в точке  существует производная
существует производная  , то
, то
Пусть задана функция  . Отметьте верные утверждения:
. Отметьте верные утверждения:
Если 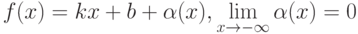 , то прямая
, то прямая 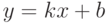
Какие утверждения справедливы:
Каким условиям должна удовлетворять функция  в теореме Лагранжа:
в теореме Лагранжа:
Чему равна  -я производная функции
-я производная функции 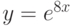
Пусть  и
и  - бесконечно малые на бесконечности функции, для которых существует предел
- бесконечно малые на бесконечности функции, для которых существует предел 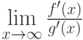 . Тогда существует предел
. Тогда существует предел
Для каких функций точка 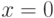 является точкой экстремума:
является точкой экстремума:
Каким условиям должны удовлетворять функции  и
и 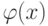 в теореме Коши:
в теореме Коши:
Как связаны многочлен Тейлора  функции
функции  , сама функция и остаточный член
, сама функция и остаточный член 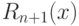 :
:
Производная функции  равна
равна
Выпуклость кривой  в точке
в точке 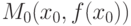 направлена вниз, если
направлена вниз, если
Пусть в точке  функция
функция  имеет первую и вторую производные. Какие условия являются достаточными, чтобы точка
имеет первую и вторую производные. Какие условия являются достаточными, чтобы точка  была точкой минимума для
была точкой минимума для  :
:
Какое равенство верно ( ):
):
Для каких из перечисленных функций  :
:
Производной функции  в данной точке
в данной точке  называется
называется
Производной функции  является функция
является функция
По определению, функция  в точке
в точке  имеет бесконечную производную
имеет бесконечную производную 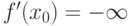 , если в этой точке
, если в этой точке
Какие из перечисленных функций непрерывны, но не дифференцируемы в точке  :
:
Каким условием должна удовлетворять функция  для того, чтобы существовала непрерывная убывающая обратная функция
для того, чтобы существовала непрерывная убывающая обратная функция  :
:
Производная 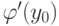 обратной функции
обратной функции  для функции
для функции  равна :
равна :
Пусть 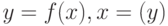 взаимно обратные функции. Тогда производная
взаимно обратные функции. Тогда производная  -го порядка
-го порядка 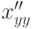 равна
равна
Дифференциал  -го порядка
-го порядка 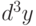 функции
функции  можно вычислить по формуле
можно вычислить по формуле
Вектор-функция  называется непрерывной при
называется непрерывной при  , если
, если
Геометрический смысл теоремы Ролля состоит в том, что существует хотя бы одна точка графика функции  , в которой касательная
, в которой касательная
Какую неопределённость нужно раскрыть при вычислении предела функции 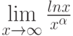 :
:
Какая из формул является выражением для остаточного члена 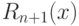 в форме Лагранжа
в форме Лагранжа
Для каких функций точка 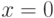 является критической точкой:
является критической точкой:
Пусть  - критическая точка
- критическая точка  , но
, но  непрерывна в
непрерывна в  . Тогда функция
. Тогда функция  в точке
в точке  имеет экстремум, если её производная
имеет экстремум, если её производная  при переходе через точку
при переходе через точку 
Пусть в точке  функция
функция  имеет первую и вторую производные. Какие утверждение справедливы:
имеет первую и вторую производные. Какие утверждение справедливы:
Наибольшее значение функция  может принимать
может принимать
Для каких функций прямая 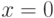 является вертикальной асимптотой:
является вертикальной асимптотой:
Если прямая 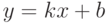 является наклонной асимптотой графика функции
является наклонной асимптотой графика функции  , то
, то  равно
равно
Для функции 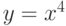 точка (0,0) графика функции является
точка (0,0) графика функции является
Второе приближение  корня уравнения
корня уравнения  на отрезке
на отрезке ![[a,b]](https://intuit.ru//sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) методом хорд вычисляется по формуле:
методом хорд вычисляется по формуле:
Каким условиям в точке  должны удовлетворять функции
должны удовлетворять функции  и
и  , чтобы выполнялось правило Лопиталя:
, чтобы выполнялось правило Лопиталя:
Какое из перечисленных уравнений является уравнением нормали к кривой  в точке с абсциссой
в точке с абсциссой  :
:
Если функция  дифференцируема в точке
дифференцируема в точке  , то она в этой точке
, то она в этой точке
Производная функции 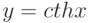 равна
равна
Какая из перечисленных функций является обратной для функции 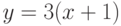
По определению, функция  в точке
в точке  имеет бесконечную производную
имеет бесконечную производную 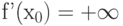 , если в этой точке
, если в этой точке
Производной функции  в данной точке
в данной точке 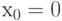 называется
называется
Производной функции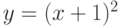 является функция
является функция
Угловой коэффициент какой прямой, проведённой в точке с абсциссой  , равен производной
, равен производной  функции
функции  :
:
Какие из перечисленных функций дифференцируемы в точке  :
:
Производная функции  равна
равна
Приближённое значение функции  в точке
в точке 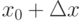 равно
равно
Если постоянный вектор  является пределом вектор-функции
является пределом вектор-функции 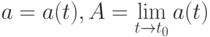 , то
, то
В условиях теоремы Лагранжа точка 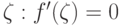
Верно ли, что функция 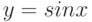 раскладывается в ряд Маклорена в любой окрестности точки
раскладывается в ряд Маклорена в любой окрестности точки 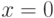
Остаточный член 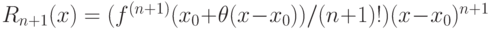 для формулы Тейлора является остаточным членом
для формулы Тейлора является остаточным членом
Пусть функция  непрерывна на [a,b] и имеет производную
непрерывна на [a,b] и имеет производную  на интервале (a,b). Какое утверждение верно:
на интервале (a,b). Какое утверждение верно:
Пусть в точке  функция
функция  имеет первую и вторую производные. Какие утверждение справедливы:
имеет первую и вторую производные. Какие утверждение справедливы:
Какие утверждения справедливы:
Для каких функций точка перегиба имеет абсциссу 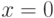 :
:
Для каких функций прямая 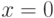 является вертикальной асимптотой:
является вертикальной асимптотой:
Если 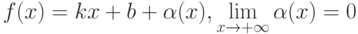 , то прямая
, то прямая 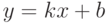
Из предложенного списка выбрать те условия, которым должна удовлетворять функция  , чтобы уравнение
, чтобы уравнение  на отрезке
на отрезке ![[a,b]](https://intuit.ru//sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) имело единственное решение:
имело единственное решение:
Если функции 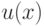 дифференцируема, а
дифференцируема, а 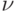 не дифференцируема в точке
не дифференцируема в точке  , то их сумма
, то их сумма 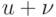 в этой точке
в этой точке
Если  , то в точке
, то в точке  производная
производная 
Остаточный член  для формулы Тейлора является остаточным членом
для формулы Тейлора является остаточным членом
Производная  -го порядка
-го порядка 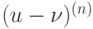 разности двух функций
разности двух функций  равна
равна
Производная функции 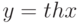 равна
равна
Правой производной 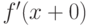 функции
функции  в данной точке
в данной точке  называется
называется
Какие из функций имеют равные правые и левые производные в точке 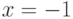 :
:
Производная  -го порядка
-го порядка 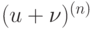 суммы двух функций
суммы двух функций  равна
равна
Для каких функций точка 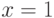 является точкой локального максимума:
является точкой локального максимума:
График дифференцируемой на интервале 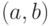 функции
функции  имеет на этом интервале выпуклость, направленную вниз, если график
имеет на этом интервале выпуклость, направленную вниз, если график  лежит в пределах интервала
лежит в пределах интервала
Прямая 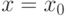 является вертикальной асимптотой графика функции
является вертикальной асимптотой графика функции  только в том случае, если
только в том случае, если
Какую неопределённость нужно раскрыть при вычислении предела функции 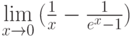 :
:
Угловой коэффициент нормали, проведённой к кривой  в точке с абсциссой
в точке с абсциссой  , равен
, равен
Каким условием должна удовлетворять функция  для того, чтобы существовала непрерывная возрастающая обратная функция
для того, чтобы существовала непрерывная возрастающая обратная функция  :
:
Какое условие нужно добавить к теореме Лагранжа, чтобы выполнялась теорема Ролля:
Функция  называется неубывающей на [a,b], если
называется неубывающей на [a,b], если ![\forall x_1, x_2 \in [a,b]: x_1 < x_2](https://intuit.ru//sites/default/files/tex_cache/e210b3b7e225b2ed9c466bd4af6172d3.png)
Пусть для функции  в окрестности точки
в окрестности точки  существует производная
существует производная  -го порядка и
-го порядка и 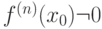 - первая отличная от нуля производная. Тогда
- первая отличная от нуля производная. Тогда  - не является точкой минимума и максимума
- не является точкой минимума и максимума  , если
, если
Каким условиям должны удовлетворять функции 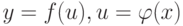 в точках
в точках  и
и 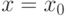 соответственно , чтобы сложная функция
соответственно , чтобы сложная функция ![y = f[\varphi (x)]](https://intuit.ru//sites/default/files/tex_cache/ead719ea19850ef1759fce07ef02772d.png) была дифференцируемой в точке
была дифференцируемой в точке 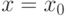 :
:
Какую неопределённость нужно раскрыть при вычислении предела функции 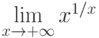 :
:
Пусть  и
и  - бесконечно большие в точке
- бесконечно большие в точке  функции, для которых существует предел
функции, для которых существует предел 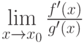 . Тогда существует предел
. Тогда существует предел
Точка  называется точкой локального минимума функции
называется точкой локального минимума функции  , если
, если
Каким условиям в точке  должны удовлетворять функции
должны удовлетворять функции  и
и  , чтобы выполнялось правило Лопиталя:
, чтобы выполнялось правило Лопиталя:
Производная  -го порядка
-го порядка 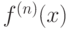 функции
функции 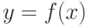 есть
есть
Какие утверждения справедливы:
Для каких из перечисленных функций  :
:
Чему равна производная функции 
Какие утверждения справедливы:
Производной функции является функция
является функция
Для каких из перечисленных функций  :
:
Чему равна  -я производная функции
-я производная функции 
Пусть функция 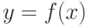 непрерывна и возрастает на
непрерывна и возрастает на ![[a,b]](https://intuit.ru//sites/default/files/tex_cache/3f25293cb3f7d82aca4fcb642825f054.png) . Тогда обратная функция
. Тогда обратная функция  :
:

 и
и  . Тогда предел
. Тогда предел 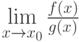
 должны выполняться, чтобы её можно было разложить в ряд Тейлора в окрестности точки
должны выполняться, чтобы её можно было разложить в ряд Тейлора в окрестности точки  :
: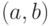 функции
функции  не имеет на этом интервале выпуклость, направленную вверх или вниз, если график
не имеет на этом интервале выпуклость, направленную вверх или вниз, если график  лежит в пределах интервала
лежит в пределах интервала задана параметрически:
задана параметрически: 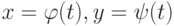 . Каким условиям должна удовлетворять функция
. Каким условиям должна удовлетворять функция 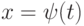 на интервале
на интервале 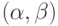 для того, чтобы существовала производная
для того, чтобы существовала производная 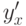 :
: , в которой касательная
, в которой касательная и
и  - бесконечно большие на бесконечности функции, для которых существует предел
- бесконечно большие на бесконечности функции, для которых существует предел 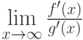 . Тогда существует предел
. Тогда существует предел и
и  , чтобы выполнялось правило Лопиталя:
, чтобы выполнялось правило Лопиталя: раз дифференцируемую в окрестности точки
раз дифференцируемую в окрестности точки  функцию
функцию  можно представить в виде формулыТейлора?
можно представить в виде формулыТейлора? - критическая точка
- критическая точка  , но
, но  непрерывна в
непрерывна в  . Тогда функция
. Тогда функция  в точке
в точке  имеет максимум, если её производная
имеет максимум, если её производная  при переходе через точку
при переходе через точку 
 функция
функция  имеет первую и вторую производные. Какие условия являются достаточными, чтобы точка
имеет первую и вторую производные. Какие условия являются достаточными, чтобы точка  была точкой максимума для
была точкой максимума для  :
: в окрестности точки
в окрестности точки  существует производная
существует производная  -го порядка и
-го порядка и 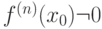 - первая отличная от нуля производная. Тогда
- первая отличная от нуля производная. Тогда  является точкой перегиба графика функции, если
является точкой перегиба графика функции, если , чтобы уравнение
, чтобы уравнение  на отрезке
на отрезке ![[a,b]](https://intuit.ru//sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) имело единственное решение:
имело единственное решение: , чтобы при применении метода хорд точка пересечения хорды с осью
, чтобы при применении метода хорд точка пересечения хорды с осью  было приближением к корню уравнения
было приближением к корню уравнения  на отрезке
на отрезке ![[a,b]](https://intuit.ru//sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) :
: , чтобы уравнение
, чтобы уравнение  на отрезке
на отрезке ![[a,b]](https://intuit.ru//sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) имело хотя бы одно решение:
имело хотя бы одно решение: и
и  на бесконечности. Тогда предел
на бесконечности. Тогда предел 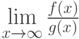
 , чтобы при применении метода касательных точка пересечения касательной с осью
, чтобы при применении метода касательных точка пересечения касательной с осью  было приближением к корню уравнения
было приближением к корню уравнения  на отрезке
на отрезке ![[a,b]](https://intuit.ru//sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) :
: в окрестности точки
в окрестности точки  существует производная
существует производная  -го порядка и
-го порядка и 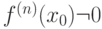 - первая отличная от нуля производная. Тогда
- первая отличная от нуля производная. Тогда  - точка минимума
- точка минимума  , если
, если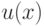 дифференцируема в точке
дифференцируема в точке  и
и 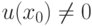 , а
, а 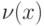 не дифференцируема в точке
не дифференцируема в точке  , то их произведение
, то их произведение  в этой точке
в этой точке задана параметрически:
задана параметрически: 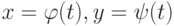 . Каким условиям должна удовлетворять функция
. Каким условиям должна удовлетворять функция 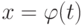 на интервале
на интервале 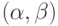 для того, чтобы существовала производная
для того, чтобы существовала производная 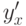 :
: - критическая точка
- критическая точка  , но
, но  непрерывна в
непрерывна в  . Тогда функция
. Тогда функция  в точке
в точке  имеет минимум, если её производная
имеет минимум, если её производная  при переходе через точку
при переходе через точку 
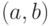 функции
функции  не имеет на этом интервале выпуклость, направленную вверх, если график
не имеет на этом интервале выпуклость, направленную вверх, если график  лежит в пределах интервала
лежит в пределах интервала в окрестности точки
в окрестности точки  существует производная
существует производная  -го порядка, непрерывная в
-го порядка, непрерывная в  и
и 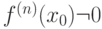 - первая отличная от нуля производная. Тогда
- первая отличная от нуля производная. Тогда  - точка максимума
- точка максимума  , если
, если и
и  - бесконечно малые на бесконечности функции, для которых существует предел
- бесконечно малые на бесконечности функции, для которых существует предел 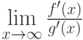 . Тогда существует предел
. Тогда существует предел функция
функция  имеет первую и вторую производные. Какие условия являются достаточными, чтобы точка
имеет первую и вторую производные. Какие условия являются достаточными, чтобы точка  была точкой минимума для
была точкой минимума для  :
: для того, чтобы существовала непрерывная убывающая обратная функция
для того, чтобы существовала непрерывная убывающая обратная функция  :
: , в которой касательная
, в которой касательная - критическая точка
- критическая точка  , но
, но  непрерывна в
непрерывна в  . Тогда функция
. Тогда функция  в точке
в точке  имеет экстремум, если её производная
имеет экстремум, если её производная  при переходе через точку
при переходе через точку 
 , чтобы уравнение
, чтобы уравнение  на отрезке
на отрезке ![[a,b]](https://intuit.ru//sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) имело единственное решение:
имело единственное решение: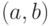 функции
функции  имеет на этом интервале выпуклость, направленную вниз, если график
имеет на этом интервале выпуклость, направленную вниз, если график  лежит в пределах интервала
лежит в пределах интервала для того, чтобы существовала непрерывная возрастающая обратная функция
для того, чтобы существовала непрерывная возрастающая обратная функция  :
: в окрестности точки
в окрестности точки  существует производная
существует производная  -го порядка и
-го порядка и 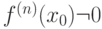 - первая отличная от нуля производная. Тогда
- первая отличная от нуля производная. Тогда  - не является точкой минимума и максимума
- не является точкой минимума и максимума  , если
, если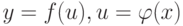 в точках
в точках  и
и 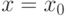 соответственно , чтобы сложная функция
соответственно , чтобы сложная функция ![y = f[\varphi (x)]](https://intuit.ru//sites/default/files/tex_cache/ead719ea19850ef1759fce07ef02772d.png) была дифференцируемой в точке
была дифференцируемой в точке 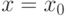 :
: и
и  - бесконечно большие в точке
- бесконечно большие в точке  функции, для которых существует предел
функции, для которых существует предел 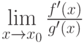 . Тогда существует предел
. Тогда существует предел