База ответов ИНТУИТ

Дифференциальное исчисление функций одной переменной

<<- Назад к вопросам

Верно ли, что n+1 раз дифференцируемую в окрестности точки x_0 функцию f(x) можно представить в виде формулыТейлора?

(Отметьте один правильный вариант ответа.)
Варианты ответа
да, всегда(Верный ответ)
нет, никогда
да, но есть исключения
Похожие вопросы
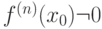Пусть для функции f(x) в окрестности точки x_0 существует производная n-го порядка, непрерывная в x_0 и f^{(n)}(x_0) \neg 0 - первая отличная от нуля производная. Тогда x_0 - точка максимума f(x), если
Пусть для функции f(x) в окрестности точки x_0 существует производная n-го порядка и f^{(n)}(x_0) \neg 0 - первая отличная от нуля производная. Тогда x_0 - не является точкой минимума и максимума f(x), если
Пусть для функции f(x) в окрестности точки x_0 существует производная n-го порядка и f^{(n)}(x_0) \neg 0 - первая отличная от нуля производная. Тогда x_0 - точка минимума f(x), если
Пусть x_0 - критическая точка f(x), но f(x) непрерывна в x_0. Тогда функция f(x) в точке x_0 имеет экстремум, если её производная f'(x) при переходе через точку x_0
Пусть x_0 - критическая точка f(x), но f(x) непрерывна в x_0. Тогда функция f(x) в точке x_0 имеет минимум, если её производная f'(x) при переходе через точку x_0
Пусть x_0 - критическая точка f(x), но f(x) непрерывна в x_0. Тогда функция f(x) в точке x_0 имеет максимум, если её производная f'(x) при переходе через точку x_0
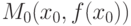Пусть для функции f(x) в окрестности точки x_0 существует производная n-го порядка и f^{(n)}(x_0) \neg 0 - первая отличная от нуля производная. Тогда M_0(x_0,f(x_0)) является точкой перегиба графика функции, если
Пусть в точке x_0 функция f(x) имеет первую и вторую производные. Какие условия являются достаточными, чтобы точка x_0 была точкой минимума для f(x):
Пусть в точке x_0 функция f(x) имеет первую и вторую производные. Какие условия являются достаточными, чтобы точка x_0 была точкой максимума для f(x):
Функция y = f(x) называется дифференцируемой в точке x_0, если приращение \Delta y можно представить в виде (A = const, \alpha (\Delta x) \to 0 \Delta x \to 0)