База ответов ИНТУИТ

Инструменты, алгоритмы и структуры данных

<<- Назад к вопросам

Рекурсивное определение функции F можно рассматривать как уравнение неподвижной точки F = h(F). Какие утверждения справедливы для этого уравнения?

(Ответ считается верным, если отмечены все правильные варианты ответов.)
Варианты ответа
решением уравнения неподвижной точки является функция h, которая, будучи примененной к графу функции F оставляет этот граф (множество пар) неизменным. (Верный ответ)
рекурсивное определение F позволяет построить функцию h(Верный ответ)
если известно решение уравнения неподвижной точки - функция h, то можно функцию F определить без использования рекурсии(Верный ответ)
функция h, также как и функция F, является рекурсивной
Похожие вопросы
Рекурсивное определение можно рассматривать как уравнение неподвижной точки F = h(F). Пусть функция h является решением этого уравнения. Какие утверждения справедливы для этой функции?
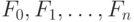Пусть функция h является решением уравнения неподвижной точки F = h(F). Это позволяет дать не рекурсивное определение функции F, аналогично тому, как определяется предел последовательности. Рассмотрим последовательность графов и связанных с ними функций F_0, F_1, … , F_n. Какие утверждения не являются справедливыми относительно такого определения F?
Пусть аргументом функции h является множество пар целых чисел. Пусть также функция h:
  • добавляет в множество пару [0,0];
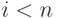  • если в множестве есть пара [i, S] и i<n, то в множество добавляется пара [i+1, S+ i +1]
    •  Для какой рекурсивно определенной функции F(n), где n>=0, функция h является решением уравнения неподвижной точки F = h(F)?
    Рекурсивное определение напоминает фокус. Рассмотрим рекурсивное определение известной в математике функции:
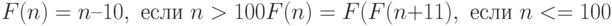
    F(n) = n – 10,\text{ если }n > 100\\ F(n) = F(F(n + 11),\text{ если }n <= 100
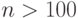    Совершенно очевидно, какие значения принимает эта функция при n> 100. А каковы ее значения при 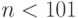n< 101? Оказывается, для таких n функция имеет одно и то же значение. Какое?
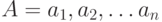    Пусть для конечного множества элементов A ={a_1, a_2,… a_n} задано ациклическое отношение r множеством пар [a_k, a_j], принадлежащих отношению. На множестве А можно построить n! различных последовательностей этих элементов - перечислений элементов. Какие утверждения справедливы относительно этих перечислений и их топологической отсортированности?
    Рассмотрим рекурсивное определение понятия "идентификатор":
    \text{идентификатор }\triangleq\text{ буква | идентификатор буква | идентификатор цифра}
    Пусть алфавит языка содержит две буквы - x и y и одну цифру -1. Индуцируя построение идентификаторов в стиле неподвижной точки, на нулевом уровне можно построить два идентификатора в соответствии с нерекурсивной частью определения, а сколько идентификаторов можно построить, принадлежащих уровню 2:
    Гарри Поттер ищет важную для него информацию. Он надеется, что она может быть в одной из книг библиотеки Хогварда, содержащей N книг. Гарри наугад выбирает книгу и просматривает ее содержимое, на что у него уходит T минут. При неудаче он повторяет поиск, выбирая новую книгу. Для такого алгоритма поиска каковы значения времени поиска: минимальное, максимальное, в среднем?
    Пусть Т - полное бинарное дерево (каждый узел не являющийся листом дерева имеет двух потомков) число листьев в котором равно 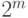2^m. Для обхода дерева применяется инфиксная процедура обхода (обойти левое дерево, обойти корень, обойти правое дерево). Каким по счету будет посещен корень дерева, если счет узлов начинается с 1)?
    Пусть разыскивается путь в графе. Содержательно можно рассматривать города, соединенные сетью дорог. Задача состоит в том, чтобы найти путь из города А в город В. Для поиска пути применяется алгоритм перебора с возвратами, реализованный в виде процедуры поиска find(path), где path - это построенный путь, начинающийся в городе А и заканчивающийся приходом в некоторый ранее не встречавшийся на построенном пути город N. 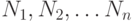Из города N дороги ведут в n городов - N_1, N_2,… N_n, не вошедшие в путь path. Какие утверждения справедливы для процедуры поиска?
    Пусть разыскивается путь в графе. Содержательно можно рассматривать города, соединенные сетью дорог. Задача состоит в том, чтобы найти путь из города А в город В. Для поиска пути применяется алгоритм перебора с возвратами, реализованный в виде процедуры поиска find(path), где path - это построенный путь, начинающийся в городе А и заканчивающийся приходом в некоторый ранее не встречавшийся на построенном пути город N. Из города N дороги ведут в n городов - N_1, N_2,… N_n, не входящие в путь path. Какие утверждения справедливы относительно возвратов в процессе поиска?