Инструменты, алгоритмы и структуры данных

Рассмотрим рекурсивное определение понятия "идентификатор":
$\text{идентификатор }\triangleq\text{ буква | идентификатор буква | идентификатор цифра}$
Пусть алфавит языка содержит две буквы - x и y и одну цифру -1. Индуцируя построение идентификаторов в стиле неподвижной точки, на нулевом уровне можно построить два идентификатора в соответствии с нерекурсивной частью определения, а сколько идентификаторов можно построить, принадлежащих уровню 2:

(Отметьте один правильный вариант ответа.)

Варианты ответа

18(Верный ответ)

Похожие вопросы

Рассмотрим язык программирования с двумя операторами - присваивания и цикла. Присваивание рассматривается в классическом варианте variable := expression и считается терминальным, не определяемым далее понятием. Грамматика языка такова:

$\text{Оператор }\triangleq\text{ Присваивание | Цикл}\\ \text{Цикл }\triangleq \text{ until (Условие) Оператор}$

Какие утверждения являются справедливыми относительно правил этой грамматики?

Рекурсивное определение напоминает фокус. Рассмотрим рекурсивное определение известной в математике функции:

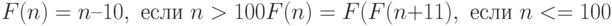
$F(n) = n – 10,\text{ если }n > 100\\ F(n) = F(F(n + 11),\text{ если }n <= 100$

Совершенно очевидно, какие значения принимает эта функция при n> 100

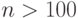. А каковы ее значения при n< 101

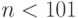? Оказывается, для таких

функция имеет одно и то же значение. Какое?

Пусть функция

является решением уравнения неподвижной точки F = h(F)

. Это позволяет дать не рекурсивное определение функции

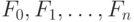, аналогично тому, как определяется предел последовательности. Рассмотрим последовательность графов и связанных с ними функций F_0, F_1, … , F_n

. Какие утверждения не являются справедливыми относительно такого определения

Рекурсивное определение можно рассматривать как уравнение неподвижной точки F = h(F)

. Пусть функция

является решением этого уравнения. Какие утверждения справедливы для этой функции?

Рекурсивное определение функции

можно рассматривать как уравнение неподвижной точки F = h(F)

. Какие утверждения справедливы для этого уравнения?

Рассмотрим конечное множество из пяти элементов. Пусть на этом множестве задано отношение r, содержащее только одну пару элементов. Сколько различных топологически отсортированных отношением r последовательностей можно построить?

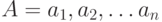Пусть для конечного множества элементов $A ={a_1, a_2,… a_n}$ задано ациклическое отношение r множеством пар [a_k, a_j]

, принадлежащих отношению. На множестве А можно построить n! различных последовательностей этих элементов - перечислений элементов. Какие утверждения справедливы относительно этих перечислений и их топологической отсортированности?

Ограничители языка являются лексемами, у которых есть только единственный образец - сам ограничитель, в то время как у таких лексем как Целое или Идентификатор число образцов бесконечно. Укажите, какие элементы не может содержать продукция БНФ?

Пусть аргументом функции

является множество пар целых чисел. Пусть также функция

добавляет в множество пару [0,0];

если в множестве есть пара [i, S]

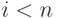, то в множество добавляется пара [i+1, S+ i +1]

Для какой рекурсивно определенной функции F(n)

, где

, функция

является решением уравнения неподвижной точки F = h(F)

Напомним, что идентификатором называется любая последовательность букв, цифр и символа подчеркивания, начинающаяся с буквы. Заметьте, это определение не рекурсивно. Какие из БНФ определений идентификатора являются корректными рекурсивными определениями?