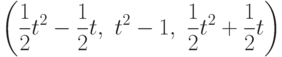Какое скалярное произведение будет иметь вектор 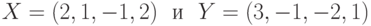 ?
?
(Отметьте один правильный вариант ответа.)
Варианты ответа
0
9(Верный ответ)
3

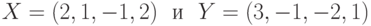 ?
?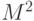 задано скалярное произведение
задано скалярное произведение  . Как будет выглядеть матрица оператора дифференцирования А и сопряженного оператора
. Как будет выглядеть матрица оператора дифференцирования А и сопряженного оператора 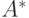 в базисе
в базисе  ?
?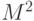 задано скалярное произведение
задано скалярное произведение  . Как будет выглядеть матрица оператора дифференцирования А и сопряженного оператора
. Как будет выглядеть матрица оператора дифференцирования А и сопряженного оператора 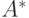 в базисе
в базисе 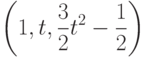
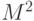 задано скалярное произведение
задано скалярное произведение  . Как будет выглядеть матрица оператора дифференцирования А и сопряженного оператора
. Как будет выглядеть матрица оператора дифференцирования А и сопряженного оператора 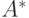 в базисе
в базисе