Найти величину касательного напряжения на поверхности обтекаемой пластинки в задаче Блазиуса используя интегральное уравнение количества движения и профиль скорости 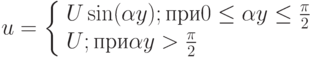 . Здесь
. Здесь  ,
, 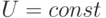
(Отметьте один правильный вариант ответа.)
Варианты ответа
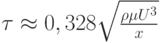 (Верный ответ)
(Верный ответ)
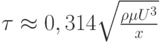
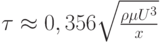

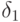 (Толщина вытеснения
(Толщина вытеснения  )
)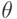 (Толщина потери импульса
(Толщина потери импульса 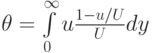 )
)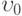 . Расстояние между плоскостями равно
. Расстояние между плоскостями равно 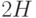 . Коэффициент вязкости:
. Коэффициент вязкости: 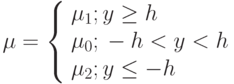 , причем
, причем  ,
,  ,
,  . Найти величину касательного напряжения
. Найти величину касательного напряжения 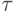 на плоскостях при соотношении
на плоскостях при соотношении  (при
(при  ,
, 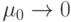 )
) (при
(при  (при
(при  при
при  при соотношении
при соотношении 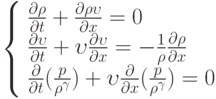 , где
, где  - постоянная;
- постоянная;  — декартова координата;
— декартова координата;  — плотность;
— плотность;  — давление;
— давление; 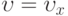 ,
,  — компоненты скорости. Пусть плоскость
— компоненты скорости. Пусть плоскость 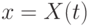 есть поверхность слабого разрыва параметров
есть поверхность слабого разрыва параметров 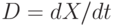 движения поверхности слабого разрыва через значения
движения поверхности слабого разрыва через значения