Математические модели механики сплошных сред - ответы
Количество вопросов - 252
При уменьшении температуры динамическая вязкость жидкостей:
Укажите размерность константы скорости для реакции второго порядка:
Укажите единицу измерения коэффициента теплопроводности:
Как называется изолированная поверхность, на которой терпят разрыв параметры, описывающие движение и состояние среды?
Укажите определение вихревого слоя:
Написать уравнение равновесия упругой среды в перемещениях при наличии температурных деформаций, если перемещения обладают осевой симметрией при плоской деформации ( )
)
Что характеризует модуль объёмного сжатия?
Определить деформацию  неравномерно нагретого упругого цилиндра с осесимметричным распределением температуры
неравномерно нагретого упругого цилиндра с осесимметричным распределением температуры 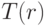 . Считать, что осевые смещения отсутствуют, т. е. имеет место плоское деформированное состояние. На внешней границе цилиндра температура равна нулю
. Считать, что осевые смещения отсутствуют, т. е. имеет место плоское деформированное состояние. На внешней границе цилиндра температура равна нулю
Найти составляющую 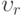 поля скоростей в осесимметричном ползущем течении вязкой жидкости между параллельными плоскостями, сближающимися с относительной скоростью
поля скоростей в осесимметричном ползущем течении вязкой жидкости между параллельными плоскостями, сближающимися с относительной скоростью  , в момент, когда расстояние между ними равно
, в момент, когда расстояние между ними равно 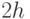 . Решение искать в виде
. Решение искать в виде 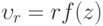 ,
, 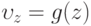 , ось
, ось  перпендикулярна слою (
перпендикулярна слою ( - уравнения плоскостей)
- уравнения плоскостей)
Определить напряжение 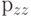 в длинной круглой трубе с внутренним
в длинной круглой трубе с внутренним  и внешним
и внешним  радиусами при плоской деформации, если температура внутри равна
радиусами при плоской деформации, если температура внутри равна 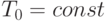 , снаружи
, снаружи 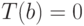 , а ее внешняя и внутренняя поверхности свободны от напряжений
, а ее внешняя и внутренняя поверхности свободны от напряжений
Определить удлинение 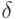 стержня первоначальной длины
стержня первоначальной длины 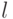 и веса
и веса  , висящего вертикально в поле силы тяжести
, висящего вертикально в поле силы тяжести
Укажите определение объёмной доли:
Сферический вихрь Хилла представляет собой осесимметричное течение без закрутки внутри сферы радиуса  , в котором вихрь имеет только азимутальную компоненту, пропорциональную расстоянию от оси симметрии
, в котором вихрь имеет только азимутальную компоненту, пропорциональную расстоянию от оси симметрии  ,
, 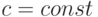 . Найти скорость обтекания сферического вихря Хилла, используя условие непрерывности поля скорости
. Найти скорость обтекания сферического вихря Хилла, используя условие непрерывности поля скорости
Уравнения Навье-Стокса состоят из:
Укажите, что утверждает теорема Гельмгольца:
Слой вязкой жидкости ограничен двумя горизонтальными бесконечными параллельными пластинами  и
и  , расстояние
, расстояние  между которыми фиксировано. Найти составляющую скорости
между которыми фиксировано. Найти составляющую скорости 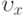 слоя, если пластина
слоя, если пластина  покоится, пластина
покоится, пластина  движется со скоростью
движется со скоростью  и давление вдоль пластин постоянно
и давление вдоль пластин постоянно
Укажите закон теплопроводности Фурье:
При увеличении давления динамическая вязкость жидкостей:
Укажите определение диффузии:
При каких видах разрыва через поверхность разрыва нет потока вещества?
Какая теорема устанавливает связь между циркуляцией скорости по замкнутому контуру и потоком вектора вихря через поверхность, натянутую на этот контур?
Перемещение электронов проводимости и дырок, обусловленное неоднородностями их концентрации в полупроводниках, происходит посредством:
Укажите условие, которое должно выполняться на поверхности разрыва:
Жидкость заполняет двугранный угол, образованный взаимно перпендикулярными плоскими стенками. Найти составляющую поля скорости 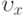 изолированной вихревой нити, параллельной ребру угла. Считать выполненными условия теоремы Томсона
изолированной вихревой нити, параллельной ребру угла. Считать выполненными условия теоремы Томсона
Укажите определение теоремы Гельмгольца о сохранении вихревых линий:
Бесконечный слой вязкой жидкости толщины  ограничен свободной поверхностью, а снизу — неподвижной плоскостью, наклоненной под углом
ограничен свободной поверхностью, а снизу — неподвижной плоскостью, наклоненной под углом  к горизонту. Под действием силы тяжести в слое происходит стационарное течение. Найти значение средней по сечению скорости в слое
к горизонту. Под действием силы тяжести в слое происходит стационарное течение. Найти значение средней по сечению скорости в слое
Поверхность, проведенная через какую-нибудь линию в жидкости и образованная из вихревых линий, называется:
Найти величину касательного напряжения на поверхности обтекаемой пластинки в задаче Блазиуса используя интегральное уравнение количества движения и профиль скорости 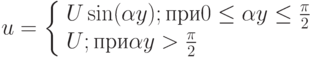 . Здесь
. Здесь  ,
, 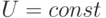
Как называется величина, характеризующая количество вещества, переносимого в единицу времени через единицу площади поверхности, перпендикулярной направлению переноса?
Укажите формулу коэффициента линейного расширения:
Как называется предельное состояние слоя вихрей, когда его толщина стремится к нулю таким образом, что циркуляция скорости по контуру элементарной площадки, ортогональной направлению распространения вихрей, стремится к некоторому постоянному значению?
Какая теорема утверждает, что если внешние силы потенциальны, то жидкая масса, составляющая вихревую трубку в какой-то момент времени, сохраняется в форме вихревой трубки и во все последующие моменты времени?
Укажите, что утверждает теорема Стокса:
Какая теорема доказывает, что если в некоторый момент времени поле скорости идеальной жидкости во всем пространстве потенциально и в дальнейшем происходит непрерывное баротропное движение, причем массовые силы обладают потенциалом, то поле скорости остается потенциальным?
Функция тока 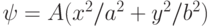 определяет плоскопараллельное течение внутри эллипса, имеющее постоянную завихренность
определяет плоскопараллельное течение внутри эллипса, имеющее постоянную завихренность  . Рассмотреть это течение относительно системы координат, вращающейся с угловой скоростью
. Рассмотреть это течение относительно системы координат, вращающейся с угловой скоростью  . Найти потенциал скорости относительного движения
. Найти потенциал скорости относительного движения
Сферический вихрь Хилла представляет собой осесимметричное течение без закрутки внутри сферы радиуса  , в котором вихрь имеет только азимутальную компоненту, пропорциональную расстоянию от оси симметрии
, в котором вихрь имеет только азимутальную компоненту, пропорциональную расстоянию от оси симметрии  ,
, 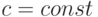 . Получить функцию тока этого течения
. Получить функцию тока этого течения
Функция тока 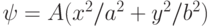 определяет плоскопараллельное течение внутри эллипса, имеющее постоянную завихренность
определяет плоскопараллельное течение внутри эллипса, имеющее постоянную завихренность  . Рассмотреть это течение относительно системы координат, вращающейся с угловой скоростью
. Рассмотреть это течение относительно системы координат, вращающейся с угловой скоростью  . Найти поле скорости переносного движения
. Найти поле скорости переносного движения
Закрытый покоящийся сосуд, заполненный неоднородной несжимаемой жидкостью, мгновенно приводится в поступательное движение со скоростью  . Для случая слабо неоднородной жидкости, когда
. Для случая слабо неоднородной жидкости, когда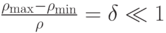 , определить вектор вихря
, определить вектор вихря  в нулевом приближении по малому параметру
в нулевом приближении по малому параметру 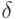
Укажите условие, которое должно быть выполнено для вихревого движения сплошной среды( -вектор скорости,
-вектор скорости,  -потенциал скорости):
-потенциал скорости):
Какой коэффициент является касательным напряжением вязкости, необходимым для поддержания разности скоростей, равной единице, между двумя параллельными слоями жидкости, разделенными расстоянием, равным единице?
Какой коэффициент является частным от деления динамического коэффициента вязкости на плотность жидкости?
При уменьшении давления динамическая вязкость жидкостей:
Какую часть полных напряжений характеризует девиатор тензора напряжений?
Бесконечный слой вязкой жидкости толщины  ограничен свободной поверхностью, а снизу — неподвижной плоскостью, наклоненной под углом
ограничен свободной поверхностью, а снизу — неподвижной плоскостью, наклоненной под углом  к горизонту. Под действием силы тяжести в слое происходит стационарное течение. Найти значение максимальной скорости в слое
к горизонту. Под действием силы тяжести в слое происходит стационарное течение. Найти значение максимальной скорости в слое
Два круглых соосно расположенных диска одинакового радиуса 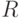 погружены в вязкую жидкость и медленно сближаются с относительной скоростью
погружены в вязкую жидкость и медленно сближаются с относительной скоростью  . Определить испытываемое дисками сопротивление, когда расстояние
. Определить испытываемое дисками сопротивление, когда расстояние 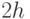 между ними мало
между ними мало
Бесконечный слой вязкой жидкости толщины  ограничен свободной поверхностью, а снизу — неподвижной плоскостью, наклоненной под углом
ограничен свободной поверхностью, а снизу — неподвижной плоскостью, наклоненной под углом  к горизонту. Под действием силы тяжести в слое происходит стационарное течение. Используя данную модель, найти значение максимальной скорости в слое при течении воды (
к горизонту. Под действием силы тяжести в слое происходит стационарное течение. Используя данную модель, найти значение максимальной скорости в слое при течении воды (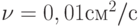 ) в канале, длина которого
) в канале, длина которого 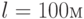 , перепад высот начала и конца над горизонтальной плоскостью
, перепад высот начала и конца над горизонтальной плоскостью  , глубина
, глубина 
Слой вязкой жидкости ограничен двумя горизонтальными бесконечными параллельными пластинами  и
и  , расстояние
, расстояние  между которыми фиксировано. Найти составляющую скорости
между которыми фиксировано. Найти составляющую скорости 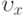 слоя, если пластина
слоя, если пластина  покоится, пластина
покоится, пластина  движется со скоростью
движется со скоростью  и задан градиент давления вдоль
и задан градиент давления вдоль 
Найти составляющую 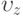 поля скоростей в осесимметричном ползущем течении вязкой жидкости между параллельными плоскостями, сближающимися с относительной скоростью
поля скоростей в осесимметричном ползущем течении вязкой жидкости между параллельными плоскостями, сближающимися с относительной скоростью  , в момент, когда расстояние между ними равно
, в момент, когда расстояние между ними равно 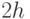 . Решение искать в виде
. Решение искать в виде 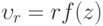 ,
, 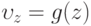 , ось
, ось  перпендикулярна слою (
перпендикулярна слою ( - уравнения плоскостей)
- уравнения плоскостей)
Слой вязкой жидкости ограничен двумя горизонтальными бесконечными параллельными пластинами  и
и  , расстояние
, расстояние  между которыми фиксировано. Найти напряжение сил трения
между которыми фиксировано. Найти напряжение сил трения 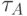 на пластинах, если пластина
на пластинах, если пластина  покоится, пластина
покоится, пластина  движется со скоростью
движется со скоростью  и давление вдоль пластин постоянно
и давление вдоль пластин постоянно
Поток газа через элемент поверхности разрыва, отнесенный на единицу площади:
При тангенциальном разрыве испытывают скачок:
Силы, с которыми действуют друг на друга газы по обеим сторонам поверхности разрыва:
При возникновении ударной волны непрерывны:
Укажите название поверхности, отделяющей области с разными значениями термодинамических параметров:
При тангенциальном разрыве непрерывна:
Одномерное адиабатическое движение идеального совершенного газа описывается системой уравнений 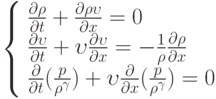 , где
, где  - постоянная;
- постоянная;  — декартова координата;
— декартова координата;  — плотность;
— плотность;  — давление;
— давление; 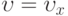 ,
,  — компоненты скорости. Пусть плоскость
— компоненты скорости. Пусть плоскость 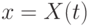 есть поверхность слабого разрыва параметров
есть поверхность слабого разрыва параметров  ,
,  и
и  . Выразить скорость
. Выразить скорость 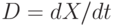 движения поверхности слабого разрыва через значения
движения поверхности слабого разрыва через значения  ,
,  ,
,  на ней.
на ней.
Идеальный совершенный газ, в котором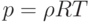 ,
,  , протекает сквозь поверхность разрыва, на которой нет внешних притоков массы, импульса и энергии. Считая потоки тепла
, протекает сквозь поверхность разрыва, на которой нет внешних притоков массы, импульса и энергии. Считая потоки тепла 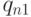 и
и 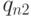 равными нулю (адиабатичность), а значения
равными нулю (адиабатичность), а значения 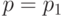 ,
, 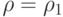 по одну сторону поверхности разрыва известными, найти изменение энтропии
по одну сторону поверхности разрыва известными, найти изменение энтропии  как функцию
как функцию 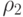
Рассмотреть стационарное течение вязкой жидкости между двумя параллельными плоскостями, движущимися в противоположных направлениях со скоростью 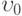 . Расстояние между плоскостями равно
. Расстояние между плоскостями равно 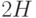 . Коэффициент вязкости:
. Коэффициент вязкости: 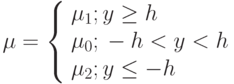 , причем
, причем  ,
,  ,
,  . Найти величину касательного напряжения
. Найти величину касательного напряжения 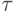 на плоскостях при соотношении
на плоскостях при соотношении  (при
(при  ,
, 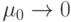 )
)
Как называется изолированная поверхность, на которой параметры, описывающие движение и состояние среды, непрерывны, но их производные терпят разрыв?
Рассмотреть стационарное течение вязкой жидкости между двумя параллельными плоскостями, движущимися в противоположных направлениях со скоростью 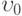 . Расстояние между плоскостями равно
. Расстояние между плоскостями равно 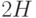 . Коэффициент вязкости:
. Коэффициент вязкости: 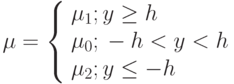 , причем
, причем  ,
,  ,
,  . Найти величину скачка скорости
. Найти величину скачка скорости  при
при  при соотношении
при соотношении  (
( ,
,  )
)
На поверхность воды падает дождь. Написать соотношения на поверхности  , разделяющей дождь и воду, рассматривая дождь как сплошную среду, воду считать несжимаемой жидкостью плотности
, разделяющей дождь и воду, рассматривая дождь как сплошную среду, воду считать несжимаемой жидкостью плотности  .Предполагая известными скорость дождя относительно поверхности
.Предполагая известными скорость дождя относительно поверхности  , а также его среднюю плотность и температуру, найти температуру в воде под поверхностью
, а также его среднюю плотность и температуру, найти температуру в воде под поверхностью 
Пограничный слой образуется:
Внутри пограничного слоя течения жидкости, вязкость жидкости влияет на течение:
Как называются решения уравнений в частных производных, зависящие от какой-нибудь одной комбинации независимых переменных и удовлетворяющие некоторому обыкновенному дифференциальному уравнению?
Укажите верное выражение независимой безразмерной переменной 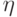 в случае автомодельного движения газа(
в случае автомодельного движения газа(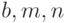 - постоянные):
- постоянные):
В задаче о распаде произвольного разрыва в газе, при 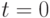 характеристики течения
характеристики течения 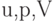 кусочно-постоянны и в области
кусочно-постоянны и в области  (
( ) равны
) равны  , а в области
, а в области  (
(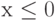 ) —
) —  . Значения
. Значения  в областях
в областях  и
и  одинаковы. Будет ли движение газа при
одинаковы. Будет ли движение газа при 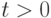 автомодельным?
автомодельным?
Как называются уравнения плоского ламинарного пограничного слоя на некоторой поверхности в несжимаемой жидкости?
При установившемся обтекании со скоростью 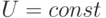 полубесконечной пластины, поставленной по потоку, функция тока для течения в пограничном слое может быть представлена в виде
полубесконечной пластины, поставленной по потоку, функция тока для течения в пограничном слое может быть представлена в виде 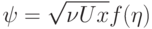 , где
, где  . Начало координат расположено в носике пластины, ось
. Начало координат расположено в носике пластины, ось  направлена вдоль пластины. Какое из указанных ниже граничных условий, следует ставить для
направлена вдоль пластины. Какое из указанных ниже граничных условий, следует ставить для 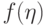 ?
?
При установившемся обтекании со скоростью 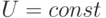 полубесконечной пластины, поставленной по потоку, функция тока для течения в пограничном слое может быть представлена в виде
полубесконечной пластины, поставленной по потоку, функция тока для течения в пограничном слое может быть представлена в виде 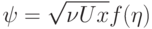 , где
, где  . Начало координат расположено в носике пластины, ось
. Начало координат расположено в носике пластины, ось  направлена вдоль пластины. Получить уравнение для
направлена вдоль пластины. Получить уравнение для 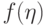
Сферический газовый пузырь радиуса  движется в вязкой жидкости с постоянной скоростью
движется в вязкой жидкости с постоянной скоростью 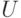 . Вычислить силу вязкого сопротивления при
. Вычислить силу вязкого сопротивления при 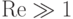
Профиль скорости в пограничном слое задан соотношениями 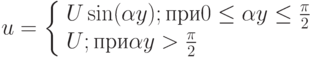 . Здесь
. Здесь  ,
, 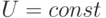 . Найти толщину вытеснения
. Найти толщину вытеснения 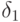 (Толщина вытеснения
(Толщина вытеснения 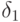 в пограничном слое определяются формулами:
в пограничном слое определяются формулами:  )
)
Вне пограничного слоя скорость имеет вид 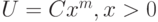 , где
, где  ,
,  — постоянные, течение в пограничном слое имеет функцию тока вида
— постоянные, течение в пограничном слое имеет функцию тока вида 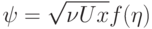 , где
, где  . Какое из указанных ниже граничных условий, следует ставить для функции
. Какое из указанных ниже граничных условий, следует ставить для функции 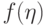 ?
?
Для абсолютно упругого материала коэффициент Пуассона равен
Что характеризует модуль Юнга?
Какая физическая величина характеризует способность материала сопротивляться изменению формы при сохранении его объёма?
Какая физическая величина характеризует способность объекта изменять свой объём под воздействием всестороннего нормального напряжения?
Тензор упругих постоянных в обобщенном законе Гука, является тензором:
Укажите выражение первого параметра Ламе  через модуль Юнга и коэффициент Пуассона:
через модуль Юнга и коэффициент Пуассона:
Призматический стержень из линейно упругого материала находится в равновесии под действием растягивающих усилий, равномерно распределенных по торцевым сечениям, и при свободных боковых гранях (простое растяжение). Найти компоненту 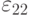 тензора деформаций при заданной величине напряжений
тензора деформаций при заданной величине напряжений  на торцах
на торцах
Образец из линейно упругого материала находится между двумя парами параллельных жестких стенок, так что его поперечные размеры не могут меняться. На торцах образца действуют однородные сжимающие напряжения  . Найти компоненту
. Найти компоненту  тензора напряжений в материале, считая, что между ним и стенками трение отсутствует
тензора напряжений в материале, считая, что между ним и стенками трение отсутствует
Напряженное состояние, описываемое шаровым тензором напряжений  , называется всесторонним сжатием. Определить относительное изменение объема
, называется всесторонним сжатием. Определить относительное изменение объема 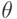
Образец из линейно упругого материала находится между двумя парами параллельных жестких стенок, так что его поперечные размеры не могут меняться. На торцах образца действуют однородные сжимающие напряжения  . Найти компоненту
. Найти компоненту 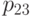 тензора напряжений в материале, считая, что между ним и стенками трение отсутствует
тензора напряжений в материале, считая, что между ним и стенками трение отсутствует
Образец из линейно упругого материала находится между двумя парами параллельных жестких стенок, так что его поперечные размеры не могут меняться. На торцах образца действуют однородные сжимающие напряжения  . Найти компоненту
. Найти компоненту  тензора деформации в материале, считая, что между ним и стенками трение отсутствует
тензора деформации в материале, считая, что между ним и стенками трение отсутствует
Коэффициент теплопроводности - это ...
Укажите, как определяется коэффициент температуропроводности( - коэффициент теплопроводности,
- коэффициент теплопроводности,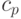 - изобарная теплоёмкость,
- изобарная теплоёмкость, - плотность):
- плотность):
Укажите единицу измерения коэффициента линейного расширения:
Укажите выражение уравнения теплопроводности:
Написать уравнение равновесия упругой среды в перемещениях при наличии температурных деформаций:
Написать уравнение равновесия упругой среды в перемещениях при наличии температурных деформаций, если перемещения обладают осевой симметрией для плоского напряженного состояния ( )
)
В круглом тонком диске радиуса 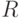 и постоянной толщины температура меняется от центра к периферии по закону
и постоянной толщины температура меняется от центра к периферии по закону  . Все поверхности диска свободны от напряжений, толщина мала, так что напряженное состояние можно считать плоским. Определить напряжение
. Все поверхности диска свободны от напряжений, толщина мала, так что напряженное состояние можно считать плоским. Определить напряжение 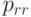 в диске, вызванное неоднородностью поля температур. На внешней границе диска
в диске, вызванное неоднородностью поля температур. На внешней границе диска 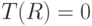
Определить деформацию 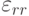 неравномерно нагретого упругого цилиндра с осесимметричным распределением температуры
неравномерно нагретого упругого цилиндра с осесимметричным распределением температуры 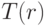 . Считать, что осевые смещения отсутствуют, т. е. имеет место плоское деформированное состояние. На внешней границе цилиндра температура равна нулю
. Считать, что осевые смещения отсутствуют, т. е. имеет место плоское деформированное состояние. На внешней границе цилиндра температура равна нулю
Определить напряжение 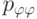 в упругом шаре радиуса
в упругом шаре радиуса  , имеющем полость радиуса
, имеющем полость радиуса  , если температура
, если температура 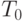 внутри полости постоянна, а температура снаружи равна нулю. Предварительно найти распределение температуры в среде. Внешняя поверхность шара и поверхность полости свободны от напряжений
внутри полости постоянна, а температура снаружи равна нулю. Предварительно найти распределение температуры в среде. Внешняя поверхность шара и поверхность полости свободны от напряжений
Как называется отношение массы растворённого вещества к массе раствора?
Укажите определение молярной объёмной концентрации:
Укажите название процесса переноса материи при отсутствии градиента концентрации частиц:
Средняя молекулярная масса смеси равна:
Константа скорости реакции - это ...
Электродиффузия - это ...
Укажите определение плотности диффузионного потока:
Укажите второй закон Фика(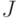 - плотность потока диффузии,
- плотность потока диффузии, 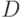 - коэффициент диффузии,
- коэффициент диффузии,  - концентрация вещества):
- концентрация вещества):
Эффект Соре обозначает явление:
Вне пограничного слоя скорость имеет вид 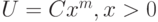 , где
, где  ,
,  — постоянные, течение в пограничном слое имеет функцию тока вида
— постоянные, течение в пограничном слое имеет функцию тока вида 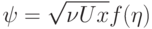 , где
, где  . Какое из указанных ниже граничных условий, следует ставить для функции
. Какое из указанных ниже граничных условий, следует ставить для функции 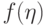 ?
?
При контактном разрыве непрерывны:
Как называется отношение объёма растворённого вещества к объёму раствора?
На стальном тросе диаметром  подвешен груз в
подвешен груз в  . Какую максимальную длину может иметь трос, чтобы он не оборвался? Предел прочности стали считать равным
. Какую максимальную длину может иметь трос, чтобы он не оборвался? Предел прочности стали считать равным  , удельный вес —
, удельный вес — 
Укажите определение вихревой пелены:
Модуль объёмного сжатия определяется как:
Поверхность разрыва — это ...
Функция тока для течения в пограничном слое в задаче Блазиуса представляется в виде 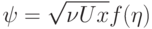 , где
, где 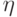 определяется как:
определяется как:
Как называется жидкость или газ, заключенная внутри вихревой поверхности, построенной на бесконечно малом замкнутом контуре?
При установившемся обтекании со скоростью 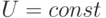 полубесконечной пластины, поставленной по потоку, функция тока для течения в пограничном слое может быть представлена в виде
полубесконечной пластины, поставленной по потоку, функция тока для течения в пограничном слое может быть представлена в виде 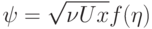 , где
, где  . Начало координат расположено в носике пластины, ось
. Начало координат расположено в носике пластины, ось  направлена вдоль пластины. Какое из указанных ниже граничных условий, следует ставить для
направлена вдоль пластины. Какое из указанных ниже граничных условий, следует ставить для 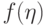 ?
?
В задаче Блазиуса рассматривается обтекание средой:
Укажите название данного уравнения: 
Жидкость заполняет двугранный угол, образованный взаимно перпендикулярными плоскими стенками. Найти траекторию изолированной вихревой нити, параллельной ребру угла. Считать выполненными условия теоремы Томсона
Одномерное адиабатическое движение идеального совершенного газа описывается системой уравнений 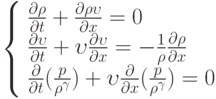 , где
, где  - постоянная;
- постоянная;  — декартова координата;
— декартова координата;  — плотность;
— плотность;  — давление;
— давление; 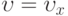 ,
,  — компоненты скорости. Пусть плоскость
— компоненты скорости. Пусть плоскость 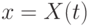 есть поверхность слабого разрыва параметров
есть поверхность слабого разрыва параметров  ,
,  и
и  . Выразить скорость
. Выразить скорость 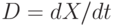 движения поверхности слабого разрыва через значения
движения поверхности слабого разрыва через значения  ,
,  ,
,  на ней.
на ней.
Математически закон Фика аналогичен:
При контактном разрыве испытывает скачок:
Слой вязкой жидкости ограничен двумя горизонтальными бесконечными параллельными пластинами  и
и  , расстояние
, расстояние  между которыми фиксировано.Найти напряжение сил трения
между которыми фиксировано.Найти напряжение сил трения 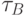 на пластинах, если пластина
на пластинах, если пластина  покоится, пластина
покоится, пластина  движется со скоростью
движется со скоростью  и задан градиент давления вдоль
и задан градиент давления вдоль 
Укажите определение динамического коэффициента вязкости:
Как называется величина, характеризующая теплопроводящие свойства материала и определяемая плотностью теплового потока при единичной разности температур между поверхностями слоя материала единичной толщины
Укажите определение теоремы Томсона:
Закрытый покоящийся сосуд, заполненный неоднородной несжимаемой жидкостью, мгновенно приводится в поступательное движение со скоростью  . Для случая слабо неоднородной жидкости, когда
. Для случая слабо неоднородной жидкости, когда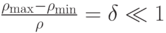 , определить вектор вихря
, определить вектор вихря  в первом приближении по малому параметру
в первом приближении по малому параметру 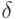
Коэффициент температуропроводности - это ...
Определить изменение объема 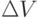 стержня первоначальной длины
стержня первоначальной длины 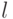 и веса
и веса  , висящего вертикально в поле силы тяжести
, висящего вертикально в поле силы тяжести
Какое условие должно выполняться на поверхности разрыва?
Как называется численная характеристика материала, равная количеству теплоты, проходящей через материал толщиной 1 м и площадью 1 кв.м за час при разности температур на двух противоположных поверхностях в 1°С?
Какой закон показывает, что тензор напряжений является линейной функцией тензора скоростей деформаций элементарного объёма жидкости?
Какая из характеристик материала совпадает со вторым параметром Ламе?
Укажите выражение уравнений Ламе:
Определить напряжение 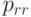 в упругом шаре радиуса
в упругом шаре радиуса  , имеющем полость радиуса
, имеющем полость радиуса  , если температура
, если температура 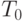 внутри полости постоянна, а температура снаружи равна нулю. Предварительно найти распределение температуры в среде. Внешняя поверхность шара и поверхность полости свободны от напряжений
внутри полости постоянна, а температура снаружи равна нулю. Предварительно найти распределение температуры в среде. Внешняя поверхность шара и поверхность полости свободны от напряжений
Укажите единицу измерения коэффициента температуропроводности:
Что характеризует модуль сдвига?
На поверхности разрыва ...
Какая теорема утверждает, что в однородной идеальной несжимаемой жидкости в поле потенциальных массовых сил циркуляция скорости по жидкому замкнутому контуру сохраняется и не зависит от времени?
Сферический вихрь Хилла представляет собой осесимметричное течение без закрутки внутри сферы радиуса  , в котором вихрь имеет только азимутальную компоненту, пропорциональную расстоянию от оси симметрии
, в котором вихрь имеет только азимутальную компоненту, пропорциональную расстоянию от оси симметрии  ,
, 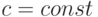 . Найти потенциал скорости обтекания сферического вихря Хилла
. Найти потенциал скорости обтекания сферического вихря Хилла
Функция тока 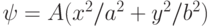 определяет плоскопараллельное течение внутри эллипса, имеющее постоянную завихренность
определяет плоскопараллельное течение внутри эллипса, имеющее постоянную завихренность  . Рассмотреть это течение относительно системы координат, вращающейся с угловой скоростью
. Рассмотреть это течение относительно системы координат, вращающейся с угловой скоростью  . Найти функцию тока относительного движения
. Найти функцию тока относительного движения
Укажите определение кинематического коэффициента вязкости:
Какой закон доказывает, что вектор теплового потока в данной индивидуальной точке сплошной среды прямо пропорционален градиенту температуры в этой же точке?
Какую часть полных напряжений характеризует шаровый тензор напряжений?
Найти стационарное движение вязкой несжимаемой жидкости в длинной горизонтальной цилиндрической трубе под действием заданного постоянного продольного перепада давления 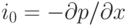 , если сечением трубы является круговое кольцо,
, если сечением трубы является круговое кольцо,  и
и  — внутренний и внешний радиусы
— внутренний и внешний радиусы
Бесконечный слой вязкой жидкости толщины  ограничен свободной поверхностью, а снизу — неподвижной плоскостью, наклоненной под углом
ограничен свободной поверхностью, а снизу — неподвижной плоскостью, наклоненной под углом  к горизонту. Под действием силы тяжести в слое происходит стационарное течение. Используя данную модель, найти значение средней по сечению скорости в слое при течении воды (
к горизонту. Под действием силы тяжести в слое происходит стационарное течение. Используя данную модель, найти значение средней по сечению скорости в слое при течении воды (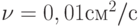 ) в канале, длина которого
) в канале, длина которого 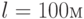 , перепад высот начала и конца над горизонтальной плоскостью
, перепад высот начала и конца над горизонтальной плоскостью  , глубина
, глубина 
Слой вязкой жидкости ограничен двумя горизонтальными бесконечными параллельными пластинами  и
и  , расстояние
, расстояние  между которыми фиксировано. Найти напряжение сил трения
между которыми фиксировано. Найти напряжение сил трения 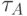 на пластинах, если пластина
на пластинах, если пластина  покоится, пластина
покоится, пластина  движется со скоростью
движется со скоростью  и задан градиент давления вдоль
и задан градиент давления вдоль 
Укажите условие, выполняющееся на поверхности разрыва:
На поверхности разрыва ...
При каком виде разрыва непрерывно давление?
При каком виде разрыва испытывает скачок давление?
Поверхность слабого разрыва - это ...
Поверхность сильного разрыва - это ...
На поверхность воды падает дождь. Написать соотношения на поверхности  , разделяющей дождь и воду, рассматривая дождь как сплошную среду, воду считать несжимаемой жидкостью плотности
, разделяющей дождь и воду, рассматривая дождь как сплошную среду, воду считать несжимаемой жидкостью плотности  .Предполагая известными скорость дождя относительно поверхности
.Предполагая известными скорость дождя относительно поверхности  , а также его среднюю плотность и температуру, найти скорость в воде под поверхностью
, а также его среднюю плотность и температуру, найти скорость в воде под поверхностью 
Как называется область течения вязкой жидкости с малой поперечной толщиной, образующаяся у поверхности обтекаемого твёрдого тела или на границе раздела двух потоков жидкости с различными скоростями, температурами или химическим составом?
При описании движения течения жидкости в тонком пограничном слое, уравнения Навье-Стокса могут быть заменены на:
Автомодельные решения - это ...
Какие из перечисленных ниже задач имеют автомодельное решение?
В каком случае задача имеет автомодельное решение?(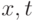 из независимой безразмерной переменной
из независимой безразмерной переменной 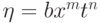 , где
, где 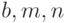 - постоянные)
- постоянные)
Чему равен вихрь на свободной поверхности, которая ограничивает плоское установившееся течение вязкой жидкости?(при  )
)
При установившемся обтекании со скоростью 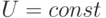 полубесконечной пластины, поставленной по потоку, функция тока для течения в пограничном слое может быть представлена в виде
полубесконечной пластины, поставленной по потоку, функция тока для течения в пограничном слое может быть представлена в виде 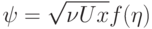 , где
, где  . Начало координат расположено в носике пластины, ось
. Начало координат расположено в носике пластины, ось  направлена вдоль пластины. Найти касательное напряжение
направлена вдоль пластины. Найти касательное напряжение 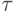 на пластине
на пластине
Вне пограничного слоя скорость имеет вид 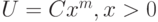 , где
, где  ,
,  — постоянные, течение в пограничном слое имеет функцию тока вида
— постоянные, течение в пограничном слое имеет функцию тока вида 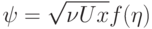 , где
, где  . Какое из указанных ниже граничных условий, следует ставить для функции
. Какое из указанных ниже граничных условий, следует ставить для функции 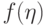 ?
?
Модуль Юнга определяется как:
Модуль сдвига определяется как:
Закон Гука устанавливает взаимосвязь:
Укажите выражение модуля всестороннего сжатия через параметры Ламе:
Призматический стержень из линейно упругого материала находится в равновесии под действием растягивающих усилий, равномерно распределенных по торцевым сечениям, и при свободных боковых гранях (простое растяжение). Найти компоненту  тензора деформаций при заданной величине напряжений
тензора деформаций при заданной величине напряжений  на торцах
на торцах
Образец из линейно упругого материала находится между двумя парами параллельных жестких стенок, так что его поперечные размеры не могут меняться. На торцах образца действуют однородные сжимающие напряжения  . Найти компоненту
. Найти компоненту 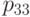 тензора напряжений в материале, считая, что между ним и стенками трение отсутствует
тензора напряжений в материале, считая, что между ним и стенками трение отсутствует
Образец из линейно упругого материала находится между двумя парами параллельных жестких стенок, так что его поперечные размеры не могут меняться. На торцах образца действуют однородные сжимающие напряжения  . Найти компоненту
. Найти компоненту 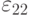 тензора деформации в материале, считая, что между ним и стенками трение отсутствует
тензора деформации в материале, считая, что между ним и стенками трение отсутствует
Укажите определение теплопроводности:
Как называется физическая величина, характеризующая скорость выравнивания температуры вещества в неравновесных тепловых процессах?
Укажите единицу измерения коэффициента объемного расширения:
Написать уравнение равновесия упругой среды в перемещениях при наличии температурных деформаций, если перемещения обладают сферической симметрией ( )
)
В круглом упругом тонком диске радиуса 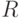 и постоянной толщины в центре имеется область радиуса
и постоянной толщины в центре имеется область радиуса  , где поддерживается постоянная температура
, где поддерживается постоянная температура 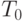 . На внешней границе диска, при
. На внешней границе диска, при  , напряжения отсутствуют и температура равна нулю. Найти радиальные напряжения в диске. Напряженное состояние можно считать плоским
, напряжения отсутствуют и температура равна нулю. Найти радиальные напряжения в диске. Напряженное состояние можно считать плоским
Как называется количество растворённого вещества в единице объёма раствора?
Какая физическая величина численно равна скорости реакции при концентрации каждого из реагирующих веществ равной 1 моль/л?
Как называется направленный перенос заряженных частиц при действии на систему внешнего электрического поля?
Укажите первый закон Фика(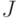 - плотность потока диффузии,
- плотность потока диффузии, 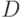 - коэффициент диффузии,
- коэффициент диффузии,  - концентрация вещества):
- концентрация вещества):
Как называется перенос компонентов газовых или жидких смесей в результате внешнего воздействия на систему градиента давления или гравитационного поля?
При увеличении температуры динамическая вязкость жидкостей:
Как называется перенос компонентов газовых или жидких смесей в результате неравномерного нагревания среды под влиянием градиента температуры?
Слой вязкой жидкости ограничен двумя горизонтальными бесконечными параллельными пластинами  и
и  , расстояние
, расстояние  между которыми фиксировано. Найти напряжение сил трения
между которыми фиксировано. Найти напряжение сил трения 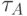 на пластинах, если обе пластины покоятся, а движение жидкости вызывается заданным градиентом давления вдоль пластин
на пластинах, если обе пластины покоятся, а движение жидкости вызывается заданным градиентом давления вдоль пластин
Одномерное адиабатическое движение идеального совершенного газа описывается системой уравнений 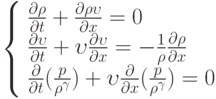 , где
, где  - постоянная;
- постоянная;  — декартова координата;
— декартова координата;  — плотность;
— плотность;  — давление;
— давление; 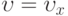 ,
,  — компоненты скорости. Пусть плоскость
— компоненты скорости. Пусть плоскость 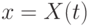 есть поверхность слабого разрыва параметров
есть поверхность слабого разрыва параметров  ,
,  и
и  . Выразить скорость
. Выразить скорость 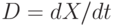 движения поверхности слабого разрыва через значения
движения поверхности слабого разрыва через значения  ,
,  ,
,  на ней.
на ней.
Принцип Сен-Венана позволяет:
Движение газа называется автомодельным, если:
Укажите размерность массовой доли:
Жидкость заполняет двугранный угол, образованный взаимно перпендикулярными плоскими стенками. Найти составляющую поля скорости  изолированной вихревой нити, параллельной ребру угла. Считать выполненными условия теоремы Томсона
изолированной вихревой нити, параллельной ребру угла. Считать выполненными условия теоремы Томсона
Укажите определение теоремы Лагранжа:
Коэффициент теплопроводности вакуума равен:
В круглом тонком диске радиуса 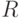 и постоянной толщины температура меняется от центра к периферии по закону
и постоянной толщины температура меняется от центра к периферии по закону  . Все поверхности диска свободны от напряжений, толщина мала, так что напряженное состояние можно считать плоским. Определить напряжение
. Все поверхности диска свободны от напряжений, толщина мала, так что напряженное состояние можно считать плоским. Определить напряжение 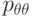 в диске, вызванное неоднородностью поля температур. На внешней границе диска
в диске, вызванное неоднородностью поля температур. На внешней границе диска 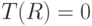
Укажите выражение обращенного закона Гука с учетом температурных напряжений( ):
):
Образец из линейно упругого материала находится между двумя парами параллельных жестких стенок, так что его поперечные размеры не могут меняться. На торцах образца действуют однородные сжимающие напряжения  . Найти компоненту
. Найти компоненту  тензора напряжений в материале, считая, что между ним и стенками трение отсутствует
тензора напряжений в материале, считая, что между ним и стенками трение отсутствует
Сферический вихрь Хилла представляет собой осесимметричное течение без закрутки внутри сферы радиуса  , в котором вихрь имеет только азимутальную компоненту, пропорциональную расстоянию от оси симметрии
, в котором вихрь имеет только азимутальную компоненту, пропорциональную расстоянию от оси симметрии  ,
, 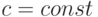 . Найти функцию тока обтекания сферического вихря Хилла
. Найти функцию тока обтекания сферического вихря Хилла
Укажите размерность молярной объёмной концентрации:
Функция тока 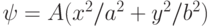 определяет плоскопараллельное течение внутри эллипса, имеющее постоянную завихренность
определяет плоскопараллельное течение внутри эллипса, имеющее постоянную завихренность  . Рассмотреть это течение относительно системы координат, вращающейся с угловой скоростью
. Рассмотреть это течение относительно системы координат, вращающейся с угловой скоростью  . Найти функцию тока переносного движения
. Найти функцию тока переносного движения
Второй закон фика связывает:
Рассмотреть стационарное течение вязкой жидкости между двумя параллельными плоскостями, движущимися в противоположных направлениях со скоростью 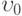 . Расстояние между плоскостями равно
. Расстояние между плоскостями равно 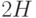 . Коэффициент вязкости:
. Коэффициент вязкости: 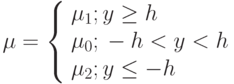 , причем
, причем  ,
,  ,
,  . Найти величину скачка скорости
. Найти величину скачка скорости  при
при  при соотношении
при соотношении  (
( ,
,  )
)
Укажите определение вихревой нити:
Какая теорема утверждает, что произвольное дифференцируемое векторное поле может быть разложено на безвихревую и соленоидальную компоненты?
Функция тока 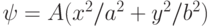 определяет плоскопараллельное течение внутри эллипса, имеющее постоянную завихренность
определяет плоскопараллельное течение внутри эллипса, имеющее постоянную завихренность  . Рассмотреть это течение относительно системы координат, вращающейся с угловой скоростью
. Рассмотреть это течение относительно системы координат, вращающейся с угловой скоростью  . Найти вектор вихря относительного движения
. Найти вектор вихря относительного движения
Укажите определение вихревой линии:
Укажите определение коэффициента теплопроводности:
Найти стационарное движение вязкой несжимаемой жидкости в длинной горизонтальной цилиндрической трубе под действием заданного постоянного продольного перепада давления 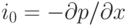 , если сечением трубы является круг радиуса
, если сечением трубы является круг радиуса 
На поверхности разрыва ...
Идеальный совершенный газ, в котором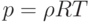 ,
,  , протекает сквозь поверхность разрыва, на которой нет внешних притоков массы, импульса и энергии. Считая потоки тепла
, протекает сквозь поверхность разрыва, на которой нет внешних притоков массы, импульса и энергии. Считая потоки тепла 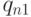 и
и 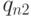 равными нулю (адиабатичность), а значения
равными нулю (адиабатичность), а значения 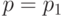 ,
, 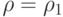 по одну сторону поверхности разрыва известными, найти
по одну сторону поверхности разрыва известными, найти  как функцию
как функцию 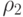 , где индекс 2 относится к величинам по другую сторону поверхности разрыва (
, где индекс 2 относится к величинам по другую сторону поверхности разрыва (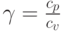 )
)
Рассмотреть стационарное течение вязкой жидкости между двумя параллельными плоскостями, движущимися в противоположных направлениях со скоростью 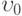 . Расстояние между плоскостями равно
. Расстояние между плоскостями равно 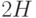 . Коэффициент вязкости:
. Коэффициент вязкости: 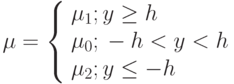 , причем
, причем  ,
,  ,
,  . Найти величину касательного напряжения
. Найти величину касательного напряжения 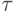 на плоскостях при соотношении
на плоскостях при соотношении  (при
(при  ,
,  )
)
Рассмотреть стационарное течение вязкой жидкости между двумя параллельными плоскостями, движущимися в противоположных направлениях со скоростью 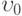 . Расстояние между плоскостями равно
. Расстояние между плоскостями равно 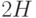 . Коэффициент вязкости:
. Коэффициент вязкости: 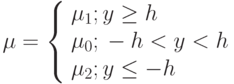 , причем
, причем  ,
,  ,
,  . Найти величину скачка скорости
. Найти величину скачка скорости  при
при  при соотношении
при соотношении  (
( ,
,  )
)
Пограничный слой - это ...
Функция тока для течения в пограничном слое в задаче Блазиуса представляется в виде:
Какая физическая величина характеризует сопротивление материала растяжению или сжатию при упругой деформации?
Призматический стержень из линейно упругого материала находится в равновесии под действием растягивающих усилий, равномерно распределенных по торцевым сечениям, и при свободных боковых гранях (простое растяжение). Найти компоненту 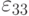 тензора деформаций при заданной величине напряжений
тензора деформаций при заданной величине напряжений  на торцах
на торцах
Образец из линейно упругого материала находится между двумя парами параллельных жестких стенок, так что его поперечные размеры не могут меняться. На торцах образца действуют однородные сжимающие напряжения  . Найти компоненту
. Найти компоненту 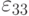 тензора деформации в материале, считая, что между ним и стенками трение отсутствует
тензора деформации в материале, считая, что между ним и стенками трение отсутствует
Укажите название данного уравнения: 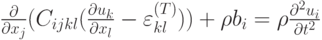
Укажите название данного уравнения: 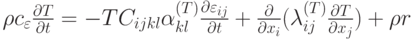
Определить деформацию 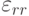 неравномерно нагретого упругого шара со сферически симметричным распределением температуры. На внешней границе шара считать
неравномерно нагретого упругого шара со сферически симметричным распределением температуры. На внешней границе шара считать 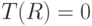
Определить напряжение 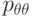 в упругом шаре радиуса
в упругом шаре радиуса  , имеющем полость радиуса
, имеющем полость радиуса  , если температура
, если температура 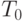 внутри полости постоянна, а температура снаружи равна нулю. Предварительно найти распределение температуры в среде. Внешняя поверхность шара и поверхность полости свободны от напряжений
внутри полости постоянна, а температура снаружи равна нулю. Предварительно найти распределение температуры в среде. Внешняя поверхность шара и поверхность полости свободны от напряжений
Укажите определение массовой доли:
Как называется общая масса смеси, деленная на общее число молей?
Укажите размерность константы скорости для реакции первого порядка:
Укажите размерность массового диффузионного потока:
Диффузионное осаждение мелких взвешенных частиц при столкновении их с молекулами газа происходит посредством:
Образец из линейно упругого материала находится между двумя парами параллельных жестких стенок, так что его поперечные размеры не могут меняться. На торцах образца действуют однородные сжимающие напряжения  . Найти компоненту
. Найти компоненту 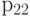 тензора напряжений в материале, считая, что между ним и стенками трение отсутствует
тензора напряжений в материале, считая, что между ним и стенками трение отсутствует
Задача Блазиуса рассматривает обтекание полубесконечной пластины:
Линия, касательные к которой совпадают с мгновенными осями вращения частиц некоторой жидкости, называется:
Слой вязкой жидкости ограничен двумя горизонтальными бесконечными параллельными пластинами  и
и  , расстояние
, расстояние  между которыми фиксировано. Найти составляющую скорости
между которыми фиксировано. Найти составляющую скорости 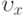 слоя, если обе пластины покоятся, а движение жидкости вызывается заданным градиентом давления вдоль пластин
слоя, если обе пластины покоятся, а движение жидкости вызывается заданным градиентом давления вдоль пластин
Движение каких жидкостей описывают уравнения Навье-Стокса?
При установившемся обтекании со скоростью 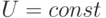 полубесконечной пластины, поставленной по потоку, функция тока для течения в пограничном слое может быть представлена в виде
полубесконечной пластины, поставленной по потоку, функция тока для течения в пограничном слое может быть представлена в виде 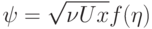 , где
, где  . Начало координат расположено в носике пластины, ось
. Начало координат расположено в носике пластины, ось  направлена вдоль пластины. Какое из указанных ниже граничных условий, следует ставить для
направлена вдоль пластины. Какое из указанных ниже граничных условий, следует ставить для 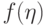 ?
?
Для абсолютно хрупкого материала коэффициент Пуассона равен:
Определить деформацию  неравномерно нагретого упругого шара со сферически симметричным распределением температуры. На внешней границе шара считать
неравномерно нагретого упругого шара со сферически симметричным распределением температуры. На внешней границе шара считать 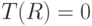
Определить напряжение 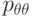 в длинной круглой трубе с внутренним
в длинной круглой трубе с внутренним  и внешним
и внешним  радиусами при плоской деформации, если температура внутри равна
радиусами при плоской деформации, если температура внутри равна 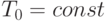 , снаружи
, снаружи 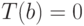 , а ее внешняя и внутренняя поверхности свободны от напряжений
, а ее внешняя и внутренняя поверхности свободны от напряжений
Размерность коэффициента диффузии:
Покоящийся газ находится в цилиндрической трубе в области  , ограниченной поршнем (
, ограниченной поршнем ( ). В момент времени
). В момент времени 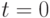 поршень начинает двигаться по закону
поршень начинает двигаться по закону 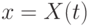 с постоянной скоростью
с постоянной скоростью 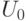 . Будет ли движение газа при
. Будет ли движение газа при 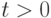 автомодельным?
автомодельным?
Определить напряжение 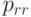 в длинной круглой трубе с внутренним
в длинной круглой трубе с внутренним  и внешним
и внешним  радиусами при плоской деформации, если температура внутри равна
радиусами при плоской деформации, если температура внутри равна 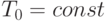 , снаружи
, снаружи 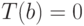 , а ее внешняя и внутренняя поверхности свободны от напряжений
, а ее внешняя и внутренняя поверхности свободны от напряжений
Функция тока 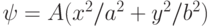 определяет плоскопараллельное течение внутри эллипса, имеющее постоянную завихренность
определяет плоскопараллельное течение внутри эллипса, имеющее постоянную завихренность  . Рассмотреть это течение относительно системы координат, вращающейся с угловой скоростью
. Рассмотреть это течение относительно системы координат, вращающейся с угловой скоростью  . Найти поле скорости относительного движения
. Найти поле скорости относительного движения
Автомодельность позволяет свести задачу к решению:
Укажите определение вихревой поверхности:
Бесконечный слой вязкой жидкости толщины  ограничен свободной поверхностью, а снизу — неподвижной плоскостью, наклоненной под углом
ограничен свободной поверхностью, а снизу — неподвижной плоскостью, наклоненной под углом  к горизонту. Под действием силы тяжести в слое происходит стационарное течение. Найти распределение скорости в слое
к горизонту. Под действием силы тяжести в слое происходит стационарное течение. Найти распределение скорости в слое
Найти поле давлений в осесимметричном ползущем течении вязкой жидкости между параллельными плоскостями, сближающимися с относительной скоростью  , в момент, когда расстояние между ними равно
, в момент, когда расстояние между ними равно 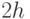 . Решение искать в виде
. Решение искать в виде 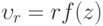 ,
, 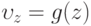 , ось
, ось  перпендикулярна слою (
перпендикулярна слою ( - уравнения плоскостей,
- уравнения плоскостей, 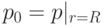 ,
, 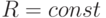 )
)
Рассмотреть стационарное течение вязкой жидкости между двумя параллельными плоскостями, движущимися в противоположных направлениях со скоростью 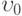 . Расстояние между плоскостями равно
. Расстояние между плоскостями равно 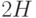 . Коэффициент вязкости:
. Коэффициент вязкости: 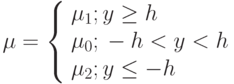 , причем
, причем  ,
,  ,
,  . Найти величину касательного напряжения
. Найти величину касательного напряжения 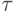 на плоскостях при соотношении
на плоскостях при соотношении  (при
(при  ,
,  )
)
Вне пограничного слоя течения жидкости, вязкость жидкости при решении задач:
Коэффициент Пуассона показывает:
Образец из линейно упругого материала находится между двумя парами параллельных жестких стенок, так что его поперечные размеры не могут меняться. На торцах образца действуют однородные сжимающие напряжения  . Найти компоненту
. Найти компоненту 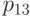 тензора напряжений в материале, считая, что между ним и стенками трение отсутствует
тензора напряжений в материале, считая, что между ним и стенками трение отсутствует
Напряженное состояние, описываемое шаровым тензором напряжений  , называется всесторонним сжатием. Определить компоненты деформации
, называется всесторонним сжатием. Определить компоненты деформации
Как называется процесс переноса материи или энергии из области с высокой концентрацией в область с низкой концентрацией?
Напряженное состояние, описываемое шаровым тензором напряжений  , называется всесторонним сжатием. Коэффициент пропорциональности между
, называется всесторонним сжатием. Коэффициент пропорциональности между  и относительным изменением объема
и относительным изменением объема 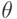 называется модулем объемного сжатия
называется модулем объемного сжатия 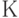 . Найти выражение для
. Найти выражение для 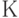 через
через 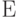 и
и 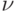
Ударная волна, распространяющаяся с постоянной скоростью 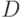 по покоящемуся газу
по покоящемуся газу  , в момент времени
, в момент времени 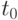 достигает поверхности контактного разрыва, отделяющей газ
достигает поверхности контактного разрыва, отделяющей газ  от газа
от газа  . Будет ли движение газов при
. Будет ли движение газов при 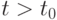 автомодельным?
автомодельным?
Профиль скорости в пограничном слое задан соотношениями 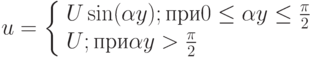 . Здесь
. Здесь  ,
, 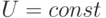 . Найти толщину потери импульса
. Найти толщину потери импульса 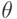 (Толщина потери импульса
(Толщина потери импульса 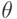 в пограничном слое определяются формулами:
в пограничном слое определяются формулами: 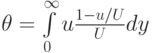 )
)
Укажите размерность объёмной доли:
Укажите формулу коэффициента объемного расширения:
Укажите, что доказывает обобщенный закон Ньютона:
На поверхность воды падает дождь. Написать соотношения на поверхности  , разделяющей дождь и воду, рассматривая дождь как сплошную среду, воду считать несжимаемой жидкостью плотности
, разделяющей дождь и воду, рассматривая дождь как сплошную среду, воду считать несжимаемой жидкостью плотности  .Предполагая известными скорость дождя относительно поверхности
.Предполагая известными скорость дождя относительно поверхности  , а также его среднюю плотность и температуру, найти давление в воде под поверхностью
, а также его среднюю плотность и температуру, найти давление в воде под поверхностью 
Как называется вихревая область среди незавихренной жидкости или газа, которая заключена между двумя близкими вихревыми поверхностями?

 )
) неравномерно нагретого упругого цилиндра с осесимметричным распределением температуры
неравномерно нагретого упругого цилиндра с осесимметричным распределением температуры 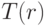 . Считать, что осевые смещения отсутствуют, т. е. имеет место плоское деформированное состояние. На внешней границе цилиндра температура равна нулю
. Считать, что осевые смещения отсутствуют, т. е. имеет место плоское деформированное состояние. На внешней границе цилиндра температура равна нулю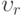 поля скоростей в осесимметричном ползущем течении вязкой жидкости между параллельными плоскостями, сближающимися с относительной скоростью
поля скоростей в осесимметричном ползущем течении вязкой жидкости между параллельными плоскостями, сближающимися с относительной скоростью  , в момент, когда расстояние между ними равно
, в момент, когда расстояние между ними равно 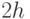 . Решение искать в виде
. Решение искать в виде 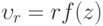 ,
, 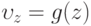 , ось
, ось  перпендикулярна слою (
перпендикулярна слою ( - уравнения плоскостей)
- уравнения плоскостей)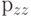 в длинной круглой трубе с внутренним
в длинной круглой трубе с внутренним  и внешним
и внешним  радиусами при плоской деформации, если температура внутри равна
радиусами при плоской деформации, если температура внутри равна 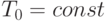 , снаружи
, снаружи 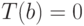 , а ее внешняя и внутренняя поверхности свободны от напряжений
, а ее внешняя и внутренняя поверхности свободны от напряжений , в котором вихрь имеет только азимутальную компоненту, пропорциональную расстоянию от оси симметрии
, в котором вихрь имеет только азимутальную компоненту, пропорциональную расстоянию от оси симметрии  ,
, 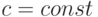 . Найти скорость обтекания сферического вихря Хилла, используя условие непрерывности поля скорости
. Найти скорость обтекания сферического вихря Хилла, используя условие непрерывности поля скорости и
и  , расстояние
, расстояние  между которыми фиксировано. Найти составляющую скорости
между которыми фиксировано. Найти составляющую скорости 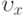 слоя, если пластина
слоя, если пластина  покоится, пластина
покоится, пластина  движется со скоростью
движется со скоростью  и давление вдоль пластин постоянно
и давление вдоль пластин постоянно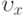 изолированной вихревой нити, параллельной ребру угла. Считать выполненными условия теоремы Томсона
изолированной вихревой нити, параллельной ребру угла. Считать выполненными условия теоремы Томсона ограничен свободной поверхностью, а снизу — неподвижной плоскостью, наклоненной под углом
ограничен свободной поверхностью, а снизу — неподвижной плоскостью, наклоненной под углом  к горизонту. Под действием силы тяжести в слое происходит стационарное течение. Найти значение средней по сечению скорости в слое
к горизонту. Под действием силы тяжести в слое происходит стационарное течение. Найти значение средней по сечению скорости в слое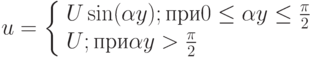 . Здесь
. Здесь  ,
, 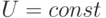
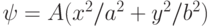 определяет плоскопараллельное течение внутри эллипса, имеющее постоянную завихренность
определяет плоскопараллельное течение внутри эллипса, имеющее постоянную завихренность  . Рассмотреть это течение относительно системы координат, вращающейся с угловой скоростью
. Рассмотреть это течение относительно системы координат, вращающейся с угловой скоростью  . Найти потенциал скорости относительного движения
. Найти потенциал скорости относительного движения , в котором вихрь имеет только азимутальную компоненту, пропорциональную расстоянию от оси симметрии
, в котором вихрь имеет только азимутальную компоненту, пропорциональную расстоянию от оси симметрии  ,
, 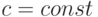 . Получить функцию тока этого течения
. Получить функцию тока этого течения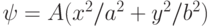 определяет плоскопараллельное течение внутри эллипса, имеющее постоянную завихренность
определяет плоскопараллельное течение внутри эллипса, имеющее постоянную завихренность  . Рассмотреть это течение относительно системы координат, вращающейся с угловой скоростью
. Рассмотреть это течение относительно системы координат, вращающейся с угловой скоростью  . Найти поле скорости переносного движения
. Найти поле скорости переносного движения . Для случая слабо неоднородной жидкости, когда
. Для случая слабо неоднородной жидкости, когда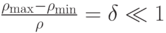 , определить вектор вихря
, определить вектор вихря  в нулевом приближении по малому параметру
в нулевом приближении по малому параметру 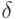
 -вектор скорости,
-вектор скорости,  -потенциал скорости):
-потенциал скорости): ограничен свободной поверхностью, а снизу — неподвижной плоскостью, наклоненной под углом
ограничен свободной поверхностью, а снизу — неподвижной плоскостью, наклоненной под углом  к горизонту. Под действием силы тяжести в слое происходит стационарное течение. Найти значение максимальной скорости в слое
к горизонту. Под действием силы тяжести в слое происходит стационарное течение. Найти значение максимальной скорости в слое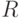 погружены в вязкую жидкость и медленно сближаются с относительной скоростью
погружены в вязкую жидкость и медленно сближаются с относительной скоростью  . Определить испытываемое дисками сопротивление, когда расстояние
. Определить испытываемое дисками сопротивление, когда расстояние 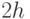 между ними мало
между ними мало ограничен свободной поверхностью, а снизу — неподвижной плоскостью, наклоненной под углом
ограничен свободной поверхностью, а снизу — неподвижной плоскостью, наклоненной под углом  к горизонту. Под действием силы тяжести в слое происходит стационарное течение. Используя данную модель, найти значение максимальной скорости в слое при течении воды (
к горизонту. Под действием силы тяжести в слое происходит стационарное течение. Используя данную модель, найти значение максимальной скорости в слое при течении воды (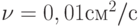 ) в канале, длина которого
) в канале, длина которого 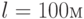 , перепад высот начала и конца над горизонтальной плоскостью
, перепад высот начала и конца над горизонтальной плоскостью  , глубина
, глубина 
 и
и  , расстояние
, расстояние  между которыми фиксировано. Найти составляющую скорости
между которыми фиксировано. Найти составляющую скорости 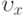 слоя, если пластина
слоя, если пластина  покоится, пластина
покоится, пластина  движется со скоростью
движется со скоростью  и задан градиент давления вдоль
и задан градиент давления вдоль 
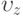 поля скоростей в осесимметричном ползущем течении вязкой жидкости между параллельными плоскостями, сближающимися с относительной скоростью
поля скоростей в осесимметричном ползущем течении вязкой жидкости между параллельными плоскостями, сближающимися с относительной скоростью  , в момент, когда расстояние между ними равно
, в момент, когда расстояние между ними равно 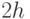 . Решение искать в виде
. Решение искать в виде 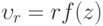 ,
, 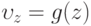 , ось
, ось  перпендикулярна слою (
перпендикулярна слою ( - уравнения плоскостей)
- уравнения плоскостей) и
и  , расстояние
, расстояние  между которыми фиксировано. Найти напряжение сил трения
между которыми фиксировано. Найти напряжение сил трения  на пластинах, если пластина
на пластинах, если пластина  покоится, пластина
покоится, пластина  движется со скоростью
движется со скоростью  и давление вдоль пластин постоянно
и давление вдоль пластин постоянно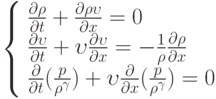 , где
, где  - постоянная;
- постоянная;  — декартова координата;
— декартова координата;  — плотность;
— плотность;  — давление;
— давление; 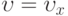 ,
,  — компоненты скорости. Пусть плоскость
— компоненты скорости. Пусть плоскость 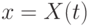 есть поверхность слабого разрыва параметров
есть поверхность слабого разрыва параметров  ,
,  и
и  . Выразить скорость
. Выразить скорость 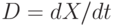 движения поверхности слабого разрыва через значения
движения поверхности слабого разрыва через значения  ,
,  ,
,  на ней.
на ней.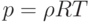 ,
,  , протекает сквозь поверхность разрыва, на которой нет внешних притоков массы, импульса и энергии. Считая потоки тепла
, протекает сквозь поверхность разрыва, на которой нет внешних притоков массы, импульса и энергии. Считая потоки тепла 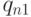 и
и 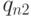 равными нулю (адиабатичность), а значения
равными нулю (адиабатичность), а значения 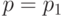 ,
, 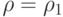 по одну сторону поверхности разрыва известными, найти изменение энтропии
по одну сторону поверхности разрыва известными, найти изменение энтропии  как функцию
как функцию 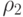
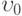 . Расстояние между плоскостями равно
. Расстояние между плоскостями равно 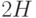 . Коэффициент вязкости:
. Коэффициент вязкости: 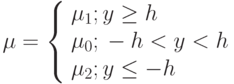 , причем
, причем  ,
,  ,
,  . Найти величину касательного напряжения
. Найти величину касательного напряжения 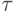 на плоскостях при соотношении
на плоскостях при соотношении  (при
(при  ,
,  )
)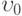 . Расстояние между плоскостями равно
. Расстояние между плоскостями равно 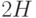 . Коэффициент вязкости:
. Коэффициент вязкости: 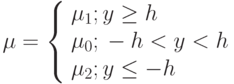 , причем
, причем  ,
,  ,
,  . Найти величину скачка скорости
. Найти величину скачка скорости  при
при  при соотношении
при соотношении  (
( ,
,  )
) , разделяющей дождь и воду, рассматривая дождь как сплошную среду, воду считать несжимаемой жидкостью плотности
, разделяющей дождь и воду, рассматривая дождь как сплошную среду, воду считать несжимаемой жидкостью плотности  .Предполагая известными скорость дождя относительно поверхности
.Предполагая известными скорость дождя относительно поверхности  , а также его среднюю плотность и температуру, найти температуру в воде под поверхностью
, а также его среднюю плотность и температуру, найти температуру в воде под поверхностью 
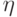 в случае автомодельного движения газа(
в случае автомодельного движения газа(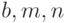 - постоянные):
- постоянные):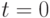 характеристики течения
характеристики течения 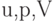 кусочно-постоянны и в области
кусочно-постоянны и в области  (
( ) равны
) равны  , а в области
, а в области  (
(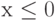 ) —
) —  . Значения
. Значения  в областях
в областях  и
и  одинаковы. Будет ли движение газа при
одинаковы. Будет ли движение газа при 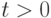 автомодельным?
автомодельным?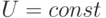 полубесконечной пластины, поставленной по потоку, функция тока для течения в пограничном слое может быть представлена в виде
полубесконечной пластины, поставленной по потоку, функция тока для течения в пограничном слое может быть представлена в виде 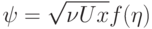 , где
, где  . Начало координат расположено в носике пластины, ось
. Начало координат расположено в носике пластины, ось  направлена вдоль пластины. Какое из указанных ниже граничных условий, следует ставить для
направлена вдоль пластины. Какое из указанных ниже граничных условий, следует ставить для 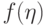 ?
?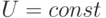 полубесконечной пластины, поставленной по потоку, функция тока для течения в пограничном слое может быть представлена в виде
полубесконечной пластины, поставленной по потоку, функция тока для течения в пограничном слое может быть представлена в виде 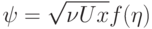 , где
, где  . Начало координат расположено в носике пластины, ось
. Начало координат расположено в носике пластины, ось  направлена вдоль пластины. Получить уравнение для
направлена вдоль пластины. Получить уравнение для 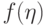
 движется в вязкой жидкости с постоянной скоростью
движется в вязкой жидкости с постоянной скоростью 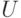 . Вычислить силу вязкого сопротивления при
. Вычислить силу вязкого сопротивления при 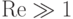
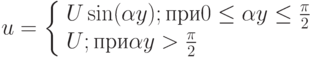 . Здесь
. Здесь  ,
, 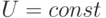 . Найти толщину вытеснения
. Найти толщину вытеснения 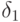 (Толщина вытеснения
(Толщина вытеснения 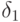 в пограничном слое определяются формулами:
в пограничном слое определяются формулами:  )
)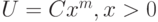 , где
, где  ,
,  — постоянные, течение в пограничном слое имеет функцию тока вида
— постоянные, течение в пограничном слое имеет функцию тока вида 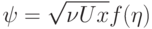 , где
, где  . Какое из указанных ниже граничных условий, следует ставить для функции
. Какое из указанных ниже граничных условий, следует ставить для функции 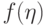 ?
?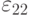 тензора деформаций при заданной величине напряжений
тензора деформаций при заданной величине напряжений  на торцах
на торцах . Найти компоненту
. Найти компоненту  тензора напряжений в материале, считая, что между ним и стенками трение отсутствует
тензора напряжений в материале, считая, что между ним и стенками трение отсутствует , называется всесторонним сжатием. Определить относительное изменение объема
, называется всесторонним сжатием. Определить относительное изменение объема 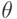
 . Найти компоненту
. Найти компоненту 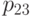 тензора напряжений в материале, считая, что между ним и стенками трение отсутствует
тензора напряжений в материале, считая, что между ним и стенками трение отсутствует . Найти компоненту
. Найти компоненту  тензора деформации в материале, считая, что между ним и стенками трение отсутствует
тензора деформации в материале, считая, что между ним и стенками трение отсутствует - коэффициент теплопроводности,
- коэффициент теплопроводности,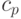 - изобарная теплоёмкость,
- изобарная теплоёмкость, - плотность):
- плотность): )
)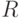 и постоянной толщины температура меняется от центра к периферии по закону
и постоянной толщины температура меняется от центра к периферии по закону  . Все поверхности диска свободны от напряжений, толщина мала, так что напряженное состояние можно считать плоским. Определить напряжение
. Все поверхности диска свободны от напряжений, толщина мала, так что напряженное состояние можно считать плоским. Определить напряжение 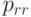 в диске, вызванное неоднородностью поля температур. На внешней границе диска
в диске, вызванное неоднородностью поля температур. На внешней границе диска 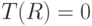
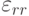 неравномерно нагретого упругого цилиндра с осесимметричным распределением температуры
неравномерно нагретого упругого цилиндра с осесимметричным распределением температуры 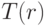 . Считать, что осевые смещения отсутствуют, т. е. имеет место плоское деформированное состояние. На внешней границе цилиндра температура равна нулю
. Считать, что осевые смещения отсутствуют, т. е. имеет место плоское деформированное состояние. На внешней границе цилиндра температура равна нулю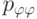 в упругом шаре радиуса
в упругом шаре радиуса  , имеющем полость радиуса
, имеющем полость радиуса  , если температура
, если температура 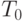 внутри полости постоянна, а температура снаружи равна нулю. Предварительно найти распределение температуры в среде. Внешняя поверхность шара и поверхность полости свободны от напряжений
внутри полости постоянна, а температура снаружи равна нулю. Предварительно найти распределение температуры в среде. Внешняя поверхность шара и поверхность полости свободны от напряжений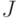 - плотность потока диффузии,
- плотность потока диффузии, 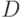 - коэффициент диффузии,
- коэффициент диффузии,  - концентрация вещества):
- концентрация вещества):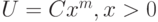 , где
, где  ,
,  — постоянные, течение в пограничном слое имеет функцию тока вида
— постоянные, течение в пограничном слое имеет функцию тока вида 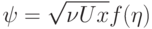 , где
, где  . Какое из указанных ниже граничных условий, следует ставить для функции
. Какое из указанных ниже граничных условий, следует ставить для функции 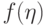 ?
? подвешен груз в
подвешен груз в  . Какую максимальную длину может иметь трос, чтобы он не оборвался? Предел прочности стали считать равным
. Какую максимальную длину может иметь трос, чтобы он не оборвался? Предел прочности стали считать равным  , удельный вес —
, удельный вес — 
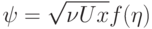 , где
, где 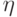 определяется как:
определяется как: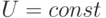 полубесконечной пластины, поставленной по потоку, функция тока для течения в пограничном слое может быть представлена в виде
полубесконечной пластины, поставленной по потоку, функция тока для течения в пограничном слое может быть представлена в виде 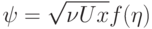 , где
, где  . Начало координат расположено в носике пластины, ось
. Начало координат расположено в носике пластины, ось  направлена вдоль пластины. Какое из указанных ниже граничных условий, следует ставить для
направлена вдоль пластины. Какое из указанных ниже граничных условий, следует ставить для 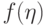 ?
?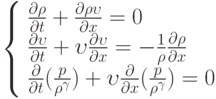 , где
, где  - постоянная;
- постоянная;  — декартова координата;
— декартова координата;  — плотность;
— плотность;  — давление;
— давление; 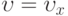 ,
,  — компоненты скорости. Пусть плоскость
— компоненты скорости. Пусть плоскость 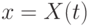 есть поверхность слабого разрыва параметров
есть поверхность слабого разрыва параметров  ,
,  и
и  . Выразить скорость
. Выразить скорость 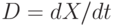 движения поверхности слабого разрыва через значения
движения поверхности слабого разрыва через значения  ,
,  ,
,  на ней.
на ней. и
и  , расстояние
, расстояние  между которыми фиксировано.Найти напряжение сил трения
между которыми фиксировано.Найти напряжение сил трения 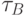 на пластинах, если пластина
на пластинах, если пластина  покоится, пластина
покоится, пластина  движется со скоростью
движется со скоростью  и задан градиент давления вдоль
и задан градиент давления вдоль 
 . Для случая слабо неоднородной жидкости, когда
. Для случая слабо неоднородной жидкости, когда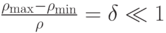 , определить вектор вихря
, определить вектор вихря  в первом приближении по малому параметру
в первом приближении по малому параметру 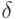
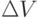 стержня первоначальной длины
стержня первоначальной длины 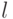 и веса
и веса  , висящего вертикально в поле силы тяжести
, висящего вертикально в поле силы тяжести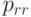 в упругом шаре радиуса
в упругом шаре радиуса  , имеющем полость радиуса
, имеющем полость радиуса  , если температура
, если температура 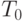 внутри полости постоянна, а температура снаружи равна нулю. Предварительно найти распределение температуры в среде. Внешняя поверхность шара и поверхность полости свободны от напряжений
внутри полости постоянна, а температура снаружи равна нулю. Предварительно найти распределение температуры в среде. Внешняя поверхность шара и поверхность полости свободны от напряжений , в котором вихрь имеет только азимутальную компоненту, пропорциональную расстоянию от оси симметрии
, в котором вихрь имеет только азимутальную компоненту, пропорциональную расстоянию от оси симметрии  ,
, 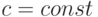 . Найти потенциал скорости обтекания сферического вихря Хилла
. Найти потенциал скорости обтекания сферического вихря Хилла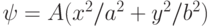 определяет плоскопараллельное течение внутри эллипса, имеющее постоянную завихренность
определяет плоскопараллельное течение внутри эллипса, имеющее постоянную завихренность  . Рассмотреть это течение относительно системы координат, вращающейся с угловой скоростью
. Рассмотреть это течение относительно системы координат, вращающейся с угловой скоростью  . Найти функцию тока относительного движения
. Найти функцию тока относительного движения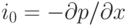 , если сечением трубы является круговое кольцо,
, если сечением трубы является круговое кольцо,  и
и  — внутренний и внешний радиусы
— внутренний и внешний радиусы ограничен свободной поверхностью, а снизу — неподвижной плоскостью, наклоненной под углом
ограничен свободной поверхностью, а снизу — неподвижной плоскостью, наклоненной под углом  к горизонту. Под действием силы тяжести в слое происходит стационарное течение. Используя данную модель, найти значение средней по сечению скорости в слое при течении воды (
к горизонту. Под действием силы тяжести в слое происходит стационарное течение. Используя данную модель, найти значение средней по сечению скорости в слое при течении воды (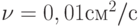 ) в канале, длина которого
) в канале, длина которого 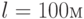 , перепад высот начала и конца над горизонтальной плоскостью
, перепад высот начала и конца над горизонтальной плоскостью  , глубина
, глубина 
 и
и  , расстояние
, расстояние  между которыми фиксировано. Найти напряжение сил трения
между которыми фиксировано. Найти напряжение сил трения 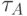 на пластинах, если пластина
на пластинах, если пластина  покоится, пластина
покоится, пластина  движется со скоростью
движется со скоростью  и задан градиент давления вдоль
и задан градиент давления вдоль 
 , разделяющей дождь и воду, рассматривая дождь как сплошную среду, воду считать несжимаемой жидкостью плотности
, разделяющей дождь и воду, рассматривая дождь как сплошную среду, воду считать несжимаемой жидкостью плотности  .Предполагая известными скорость дождя относительно поверхности
.Предполагая известными скорость дождя относительно поверхности  , а также его среднюю плотность и температуру, найти скорость в воде под поверхностью
, а также его среднюю плотность и температуру, найти скорость в воде под поверхностью 
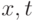 из независимой безразмерной переменной
из независимой безразмерной переменной 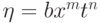 , где
, где 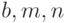 - постоянные)
- постоянные) )
)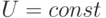 полубесконечной пластины, поставленной по потоку, функция тока для течения в пограничном слое может быть представлена в виде
полубесконечной пластины, поставленной по потоку, функция тока для течения в пограничном слое может быть представлена в виде 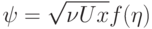 , где
, где  . Начало координат расположено в носике пластины, ось
. Начало координат расположено в носике пластины, ось  направлена вдоль пластины. Найти касательное напряжение
направлена вдоль пластины. Найти касательное напряжение 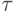 на пластине
на пластине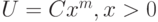 , где
, где  ,
,  — постоянные, течение в пограничном слое имеет функцию тока вида
— постоянные, течение в пограничном слое имеет функцию тока вида 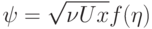 , где
, где  . Какое из указанных ниже граничных условий, следует ставить для функции
. Какое из указанных ниже граничных условий, следует ставить для функции 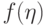 ?
? тензора деформаций при заданной величине напряжений
тензора деформаций при заданной величине напряжений  на торцах
на торцах . Найти компоненту
. Найти компоненту 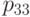 тензора напряжений в материале, считая, что между ним и стенками трение отсутствует
тензора напряжений в материале, считая, что между ним и стенками трение отсутствует . Найти компоненту
. Найти компоненту 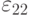 тензора деформации в материале, считая, что между ним и стенками трение отсутствует
тензора деформации в материале, считая, что между ним и стенками трение отсутствует )
) и постоянной толщины в центре имеется область радиуса
и постоянной толщины в центре имеется область радиуса  , где поддерживается постоянная температура
, где поддерживается постоянная температура  . На внешней границе диска, при
. На внешней границе диска, при  , напряжения отсутствуют и температура равна нулю. Найти радиальные напряжения в диске. Напряженное состояние можно считать плоским
, напряжения отсутствуют и температура равна нулю. Найти радиальные напряжения в диске. Напряженное состояние можно считать плоским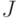 - плотность потока диффузии,
- плотность потока диффузии, 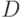 - коэффициент диффузии,
- коэффициент диффузии,  - концентрация вещества):
- концентрация вещества): и
и  , расстояние
, расстояние  между которыми фиксировано. Найти напряжение сил трения
между которыми фиксировано. Найти напряжение сил трения  на пластинах, если обе пластины покоятся, а движение жидкости вызывается заданным градиентом давления вдоль пластин
на пластинах, если обе пластины покоятся, а движение жидкости вызывается заданным градиентом давления вдоль пластин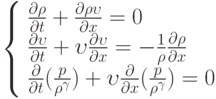 , где
, где  - постоянная;
- постоянная;  — декартова координата;
— декартова координата;  — плотность;
— плотность;  — давление;
— давление; 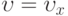 ,
,  — компоненты скорости. Пусть плоскость
— компоненты скорости. Пусть плоскость 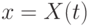 есть поверхность слабого разрыва параметров
есть поверхность слабого разрыва параметров  ,
,  и
и  . Выразить скорость
. Выразить скорость 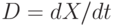 движения поверхности слабого разрыва через значения
движения поверхности слабого разрыва через значения  ,
,  ,
,  на ней.
на ней. изолированной вихревой нити, параллельной ребру угла. Считать выполненными условия теоремы Томсона
изолированной вихревой нити, параллельной ребру угла. Считать выполненными условия теоремы Томсона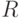 и постоянной толщины температура меняется от центра к периферии по закону
и постоянной толщины температура меняется от центра к периферии по закону  . Все поверхности диска свободны от напряжений, толщина мала, так что напряженное состояние можно считать плоским. Определить напряжение
. Все поверхности диска свободны от напряжений, толщина мала, так что напряженное состояние можно считать плоским. Определить напряжение 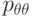 в диске, вызванное неоднородностью поля температур. На внешней границе диска
в диске, вызванное неоднородностью поля температур. На внешней границе диска 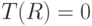
 . Найти компоненту
. Найти компоненту  тензора напряжений в материале, считая, что между ним и стенками трение отсутствует
тензора напряжений в материале, считая, что между ним и стенками трение отсутствует , в котором вихрь имеет только азимутальную компоненту, пропорциональную расстоянию от оси симметрии
, в котором вихрь имеет только азимутальную компоненту, пропорциональную расстоянию от оси симметрии  ,
,  . Найти функцию тока обтекания сферического вихря Хилла
. Найти функцию тока обтекания сферического вихря Хилла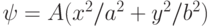 определяет плоскопараллельное течение внутри эллипса, имеющее постоянную завихренность
определяет плоскопараллельное течение внутри эллипса, имеющее постоянную завихренность  . Рассмотреть это течение относительно системы координат, вращающейся с угловой скоростью
. Рассмотреть это течение относительно системы координат, вращающейся с угловой скоростью  . Найти функцию тока переносного движения
. Найти функцию тока переносного движения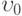 . Расстояние между плоскостями равно
. Расстояние между плоскостями равно 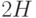 . Коэффициент вязкости:
. Коэффициент вязкости: 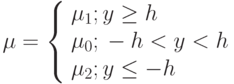 , причем
, причем  ,
,  ,
,  . Найти величину скачка скорости
. Найти величину скачка скорости  при
при  при соотношении
при соотношении  (
( ,
,  )
)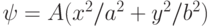 определяет плоскопараллельное течение внутри эллипса, имеющее постоянную завихренность
определяет плоскопараллельное течение внутри эллипса, имеющее постоянную завихренность  . Рассмотреть это течение относительно системы координат, вращающейся с угловой скоростью
. Рассмотреть это течение относительно системы координат, вращающейся с угловой скоростью  . Найти вектор вихря относительного движения
. Найти вектор вихря относительного движения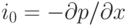 , если сечением трубы является круг радиуса
, если сечением трубы является круг радиуса 
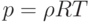 ,
,  , протекает сквозь поверхность разрыва, на которой нет внешних притоков массы, импульса и энергии. Считая потоки тепла
, протекает сквозь поверхность разрыва, на которой нет внешних притоков массы, импульса и энергии. Считая потоки тепла  и
и  равными нулю (адиабатичность), а значения
равными нулю (адиабатичность), а значения 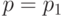 ,
, 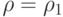 по одну сторону поверхности разрыва известными, найти
по одну сторону поверхности разрыва известными, найти  как функцию
как функцию 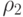 , где индекс 2 относится к величинам по другую сторону поверхности разрыва (
, где индекс 2 относится к величинам по другую сторону поверхности разрыва (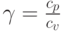 )
)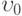 . Расстояние между плоскостями равно
. Расстояние между плоскостями равно 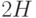 . Коэффициент вязкости:
. Коэффициент вязкости: 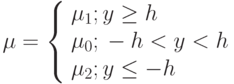 , причем
, причем  ,
,  ,
,  . Найти величину касательного напряжения
. Найти величину касательного напряжения  на плоскостях при соотношении
на плоскостях при соотношении  (при
(при  ,
,  )
)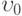 . Расстояние между плоскостями равно
. Расстояние между плоскостями равно 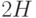 . Коэффициент вязкости:
. Коэффициент вязкости: 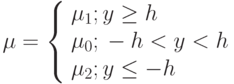 , причем
, причем  ,
,  ,
,  . Найти величину скачка скорости
. Найти величину скачка скорости  при
при  при соотношении
при соотношении  (
( ,
,  )
)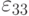 тензора деформаций при заданной величине напряжений
тензора деформаций при заданной величине напряжений  на торцах
на торцах . Найти компоненту
. Найти компоненту 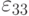 тензора деформации в материале, считая, что между ним и стенками трение отсутствует
тензора деформации в материале, считая, что между ним и стенками трение отсутствует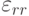 неравномерно нагретого упругого шара со сферически симметричным распределением температуры. На внешней границе шара считать
неравномерно нагретого упругого шара со сферически симметричным распределением температуры. На внешней границе шара считать 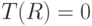
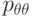 в упругом шаре радиуса
в упругом шаре радиуса  , имеющем полость радиуса
, имеющем полость радиуса  , если температура
, если температура 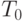 внутри полости постоянна, а температура снаружи равна нулю. Предварительно найти распределение температуры в среде. Внешняя поверхность шара и поверхность полости свободны от напряжений
внутри полости постоянна, а температура снаружи равна нулю. Предварительно найти распределение температуры в среде. Внешняя поверхность шара и поверхность полости свободны от напряжений . Найти компоненту
. Найти компоненту 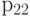 тензора напряжений в материале, считая, что между ним и стенками трение отсутствует
тензора напряжений в материале, считая, что между ним и стенками трение отсутствует и
и  , расстояние
, расстояние  между которыми фиксировано. Найти составляющую скорости
между которыми фиксировано. Найти составляющую скорости 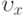 слоя, если обе пластины покоятся, а движение жидкости вызывается заданным градиентом давления вдоль пластин
слоя, если обе пластины покоятся, а движение жидкости вызывается заданным градиентом давления вдоль пластин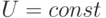 полубесконечной пластины, поставленной по потоку, функция тока для течения в пограничном слое может быть представлена в виде
полубесконечной пластины, поставленной по потоку, функция тока для течения в пограничном слое может быть представлена в виде 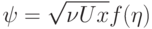 , где
, где  . Начало координат расположено в носике пластины, ось
. Начало координат расположено в носике пластины, ось  направлена вдоль пластины. Какое из указанных ниже граничных условий, следует ставить для
направлена вдоль пластины. Какое из указанных ниже граничных условий, следует ставить для 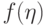 ?
? неравномерно нагретого упругого шара со сферически симметричным распределением температуры. На внешней границе шара считать
неравномерно нагретого упругого шара со сферически симметричным распределением температуры. На внешней границе шара считать 
 в длинной круглой трубе с внутренним
в длинной круглой трубе с внутренним  и внешним
и внешним  радиусами при плоской деформации, если температура внутри равна
радиусами при плоской деформации, если температура внутри равна 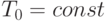 , снаружи
, снаружи 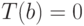 , а ее внешняя и внутренняя поверхности свободны от напряжений
, а ее внешняя и внутренняя поверхности свободны от напряжений , ограниченной поршнем (
, ограниченной поршнем ( ). В момент времени
). В момент времени 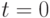 поршень начинает двигаться по закону
поршень начинает двигаться по закону 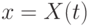 с постоянной скоростью
с постоянной скоростью 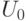 . Будет ли движение газа при
. Будет ли движение газа при 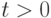 автомодельным?
автомодельным?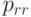 в длинной круглой трубе с внутренним
в длинной круглой трубе с внутренним  и внешним
и внешним  радиусами при плоской деформации, если температура внутри равна
радиусами при плоской деформации, если температура внутри равна 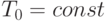 , снаружи
, снаружи 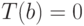 , а ее внешняя и внутренняя поверхности свободны от напряжений
, а ее внешняя и внутренняя поверхности свободны от напряжений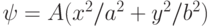 определяет плоскопараллельное течение внутри эллипса, имеющее постоянную завихренность
определяет плоскопараллельное течение внутри эллипса, имеющее постоянную завихренность  . Рассмотреть это течение относительно системы координат, вращающейся с угловой скоростью
. Рассмотреть это течение относительно системы координат, вращающейся с угловой скоростью  . Найти поле скорости относительного движения
. Найти поле скорости относительного движения ограничен свободной поверхностью, а снизу — неподвижной плоскостью, наклоненной под углом
ограничен свободной поверхностью, а снизу — неподвижной плоскостью, наклоненной под углом  к горизонту. Под действием силы тяжести в слое происходит стационарное течение. Найти распределение скорости в слое
к горизонту. Под действием силы тяжести в слое происходит стационарное течение. Найти распределение скорости в слое , в момент, когда расстояние между ними равно
, в момент, когда расстояние между ними равно  . Решение искать в виде
. Решение искать в виде 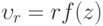 ,
, 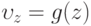 , ось
, ось  перпендикулярна слою (
перпендикулярна слою ( - уравнения плоскостей,
- уравнения плоскостей, 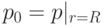 ,
, 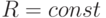 )
) . Расстояние между плоскостями равно
. Расстояние между плоскостями равно 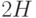 . Коэффициент вязкости:
. Коэффициент вязкости: 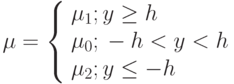 , причем
, причем  ,
,  ,
,  . Найти величину касательного напряжения
. Найти величину касательного напряжения  на плоскостях при соотношении
на плоскостях при соотношении  (при
(при  ,
,  )
) . Найти компоненту
. Найти компоненту 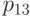 тензора напряжений в материале, считая, что между ним и стенками трение отсутствует
тензора напряжений в материале, считая, что между ним и стенками трение отсутствует , называется всесторонним сжатием. Определить компоненты деформации
, называется всесторонним сжатием. Определить компоненты деформации , называется всесторонним сжатием. Коэффициент пропорциональности между
, называется всесторонним сжатием. Коэффициент пропорциональности между  и относительным изменением объема
и относительным изменением объема 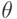 называется модулем объемного сжатия
называется модулем объемного сжатия 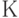 . Найти выражение для
. Найти выражение для 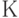 через
через 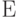 и
и 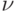
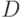 по покоящемуся газу
по покоящемуся газу  , в момент времени
, в момент времени 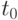 достигает поверхности контактного разрыва, отделяющей газ
достигает поверхности контактного разрыва, отделяющей газ  от газа
от газа  . Будет ли движение газов при
. Будет ли движение газов при 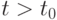 автомодельным?
автомодельным?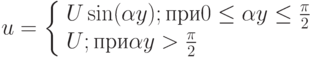 . Здесь
. Здесь  ,
,  . Найти толщину потери импульса
. Найти толщину потери импульса  (Толщина потери импульса
(Толщина потери импульса  в пограничном слое определяются формулами:
в пограничном слое определяются формулами: 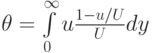 )
) , разделяющей дождь и воду, рассматривая дождь как сплошную среду, воду считать несжимаемой жидкостью плотности
, разделяющей дождь и воду, рассматривая дождь как сплошную среду, воду считать несжимаемой жидкостью плотности  .Предполагая известными скорость дождя относительно поверхности
.Предполагая известными скорость дождя относительно поверхности  , а также его среднюю плотность и температуру, найти давление в воде под поверхностью
, а также его среднюю плотность и температуру, найти давление в воде под поверхностью 