Укажите верное выражение независимой безразмерной переменной 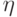 в случае автомодельного движения газа(
в случае автомодельного движения газа(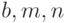 - постоянные):
- постоянные):
(Отметьте один правильный вариант ответа.)
Варианты ответа

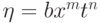 (Верный ответ)
(Верный ответ)


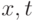 из независимой безразмерной переменной
из независимой безразмерной переменной 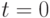 характеристики течения
характеристики течения 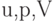 кусочно-постоянны и в области
кусочно-постоянны и в области  (
( ) равны
) равны  , а в области
, а в области  (
(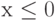 ) —
) —  . Значения
. Значения  в областях
в областях 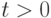 автомодельным?
автомодельным?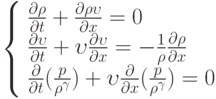 , где
, где  — декартова координата;
— декартова координата;  — плотность;
— плотность;  — давление;
— давление; 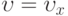 ,
,  — компоненты скорости. Пусть плоскость
— компоненты скорости. Пусть плоскость 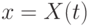 есть поверхность слабого разрыва параметров
есть поверхность слабого разрыва параметров  . Выразить скорость
. Выразить скорость 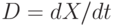 движения поверхности слабого разрыва через значения
движения поверхности слабого разрыва через значения  ). В момент времени
). В момент времени 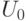 . Будет ли движение газа при
. Будет ли движение газа при 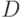 по покоящемуся газу
по покоящемуся газу 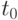 достигает поверхности контактного разрыва, отделяющей газ
достигает поверхности контактного разрыва, отделяющей газ 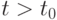 автомодельным?
автомодельным?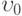 . Расстояние между плоскостями равно
. Расстояние между плоскостями равно 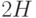 . Коэффициент вязкости:
. Коэффициент вязкости: 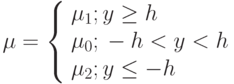 , причем
, причем  ,
,  ,
,  . Найти величину скачка скорости
. Найти величину скачка скорости  при соотношении
при соотношении  (
( ,
, 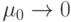 )
) (
( (
(