Найти стационарное движение вязкой несжимаемой жидкости в длинной горизонтальной цилиндрической трубе под действием заданного постоянного продольного перепада давления 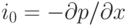 , если сечением трубы является круг радиуса
, если сечением трубы является круг радиуса 
(Отметьте один правильный вариант ответа.)
Варианты ответа


 (Верный ответ)
(Верный ответ)

 — внутренний и внешний радиусы
— внутренний и внешний радиусы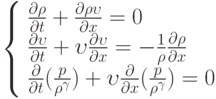 , где
, где  - постоянная;
- постоянная;  — декартова координата;
— декартова координата;  — плотность;
— плотность;  — давление;
— давление; 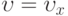 ,
,  — компоненты скорости. Пусть плоскость
— компоненты скорости. Пусть плоскость 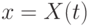 есть поверхность слабого разрыва параметров
есть поверхность слабого разрыва параметров  . Выразить скорость
. Выразить скорость 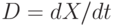 движения поверхности слабого разрыва через значения
движения поверхности слабого разрыва через значения  ограничен свободной поверхностью, а снизу — неподвижной плоскостью, наклоненной под углом
ограничен свободной поверхностью, а снизу — неподвижной плоскостью, наклоненной под углом  к горизонту. Под действием силы тяжести в слое происходит стационарное течение. Используя данную модель, найти значение максимальной скорости в слое при течении воды (
к горизонту. Под действием силы тяжести в слое происходит стационарное течение. Используя данную модель, найти значение максимальной скорости в слое при течении воды (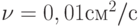 ) в канале, длина которого
) в канале, длина которого 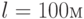 , перепад высот начала и конца над горизонтальной плоскостью
, перепад высот начала и конца над горизонтальной плоскостью  , глубина
, глубина 
 и
и  , расстояние
, расстояние  между которыми фиксировано. Найти напряжение сил трения
между которыми фиксировано. Найти напряжение сил трения 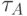 на пластинах, если обе пластины покоятся, а движение жидкости вызывается заданным градиентом давления вдоль пластин
на пластинах, если обе пластины покоятся, а движение жидкости вызывается заданным градиентом давления вдоль пластин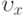 слоя, если обе пластины покоятся, а движение жидкости вызывается заданным градиентом давления вдоль пластин
слоя, если обе пластины покоятся, а движение жидкости вызывается заданным градиентом давления вдоль пластин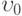 . Расстояние между плоскостями равно
. Расстояние между плоскостями равно 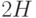 . Коэффициент вязкости:
. Коэффициент вязкости: 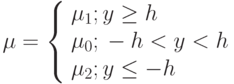 , причем
, причем  ,
,  ,
,  . Найти величину скачка скорости
. Найти величину скачка скорости  при соотношении
при соотношении  (
( ,
, 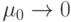 )
) (
(