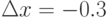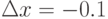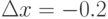Какое выражение является многочленом Тейлора  для
для  раз дифференцируемой в окрестности точки
раз дифференцируемой в окрестности точки 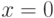 функции
функции 
(Отметьте один правильный вариант ответа.)
Варианты ответа

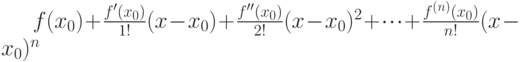 (Верный ответ)
(Верный ответ)
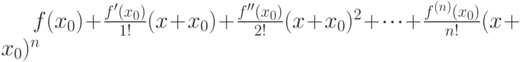
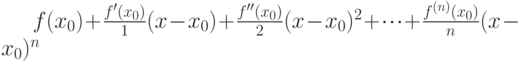

 в окрестности точки
в окрестности точки  существует производная
существует производная 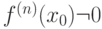 - первая отличная от нуля производная. Тогда
- первая отличная от нуля производная. Тогда 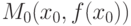 является точкой перегиба графика функции, если
является точкой перегиба графика функции, если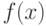 вычислите дифференциал
вычислите дифференциал 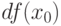 и приращение функции
и приращение функции 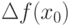 в заданной точке
в заданной точке 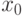 при приращении аргумента
при приращении аргумента  . В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой:
. В качестве ответа введите относительную погрешность дифференциала к приращению функции. Округлите значение до 4 знаков после запятой:  ,
, 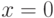 ,
, 

 ,
,