Если в точке  существует производная
существует производная  , то
, то
(Отметьте один правильный вариант ответа.)
Варианты ответа
производная в этой точке не равна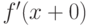 или
или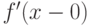
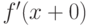 или
или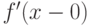
производная в этой точке равна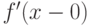 (Верный ответ)
(Верный ответ)
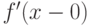 (Верный ответ)
(Верный ответ)
не существует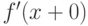
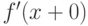

 - критическая точка
- критическая точка  , но
, но  -го порядка, непрерывная в
-го порядка, непрерывная в 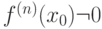 - первая отличная от нуля производная. Тогда
- первая отличная от нуля производная. Тогда ![\left[x\right]](https://intuit.ru//sites/default/files/tex_cache/fed5f6dcdaa57752ef9a484febad21d3.png) - целая часть от
- целая часть от 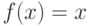 если
если  и
и 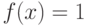 , если
, если 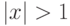
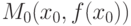 является точкой перегиба графика функции, если
является точкой перегиба графика функции, если , то в точке
, то в точке