Пусть функции 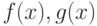 определены в некоторой окрестности точки
определены в некоторой окрестности точки  и
и 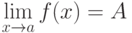 . Тогда
. Тогда
(Ответ считается верным, если отмечены все правильные варианты ответов.)
Варианты ответа
![\overline{\exists} \lim\limits_{x \to a} {[f(x) + g(x)]}](https://intuit.ru//sites/default/files/tex_cache/ec1f29b6178a65b9076fe4a1efb7d0a8.png) , если
, если 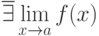 (Верный ответ)
(Верный ответ)
![\lim\limits_{x \to a} {[f(x) + g(x)]} = A + B](https://intuit.ru//sites/default/files/tex_cache/3f44e0f3f004ec14e3dcdebd7e5845bd.png) , если
, если  (Верный ответ)
(Верный ответ)
![\lim\limits_{x \to a} {[f(x) - g(x)]} = + \infty](https://intuit.ru//sites/default/files/tex_cache/1d084cb12636f97cf7601c359c96e6c2.png) , если
, если 

 определена в некоторой окрестности точки
определена в некоторой окрестности точки 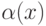 - б.м.ф. при
- б.м.ф. при 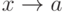 )
) . Тогда (
. Тогда ( существует производная
существует производная  -го порядка и
-го порядка и 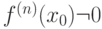 - первая отличная от нуля производная. Тогда
- первая отличная от нуля производная. Тогда 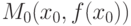 является точкой перегиба графика функции, если
является точкой перегиба графика функции, если - окрестности точки
- окрестности точки  , то в некоторой окрестности точки
, то в некоторой окрестности точки