Функция  - интегрируема по Риману на
- интегрируема по Риману на ![[a,b]](https://intuit.ru//sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) . Тогда предел интегральных сумм этой функции
. Тогда предел интегральных сумм этой функции
(Отметьте один правильный вариант ответа.)
Варианты ответа
равен нулю
может равняться бесконечности
может не существовать
существует и конечен(Верный ответ)

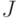 называется пределом интегральных сумм
называется пределом интегральных сумм  функции
функции  для любого разбиения
для любого разбиения ![[a,b]:\Delta x_k<\delta](https://intuit.ru//sites/default/files/tex_cache/c411055598b353d591251014a426935c.png)
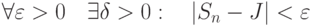
![[a,c]](https://intuit.ru//sites/default/files/tex_cache/209f61583177d88b1f24c85f6a43c6ff.png) , но не интегрируема на отрезке
, но не интегрируема на отрезке ![[c,b]](https://intuit.ru//sites/default/files/tex_cache/d6033df87877013a91e322ce6a5bc181.png) . Тогда она на отрезке
. Тогда она на отрезке  на заданном отрезке
на заданном отрезке  равных промежутков точками
равных промежутков точками 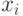 ,
,  ,
, 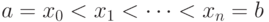 и выбирая значения
и выбирая значения  ,
,  указанным способом.
указанным способом. 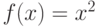 на отрезке
на отрезке ![[0,3]](https://intuit.ru//sites/default/files/tex_cache/ed9c05fe24c0f49f5d73f494a921e0c4.png) , значения
, значения 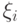 ,
, 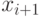 .
.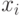 .
. на отрезке
на отрезке ![[1,6]](https://intuit.ru//sites/default/files/tex_cache/2bccbe7a6d329cdc83f6595403ff524e.png) , значения
, значения 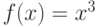 на отрезке
на отрезке ![[-2,3]](https://intuit.ru//sites/default/files/tex_cache/b0d7f8a67eadd14f5ecf59564e6b1c08.png) , значения
, значения