Площадь, ограниченная кривой 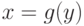 и осью ординат, вычисляется по формуле
и осью ординат, вычисляется по формуле 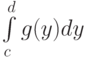 . Пределы интегрирования
. Пределы интегрирования  - это:
- это:
(Ответ считается верным, если отмечены все правильные варианты ответов.)
Варианты ответа
корни уравнения 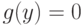 (Верный ответ)
(Верный ответ)
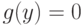 (Верный ответ)
(Верный ответ)
корни уравнения 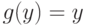
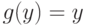
точки пересечения кривой с осью 

точки пересечения кривой с осью 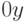 (Верный ответ)
(Верный ответ)
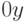 (Верный ответ)
(Верный ответ)

 для функции
для функции  на заданном отрезке
на заданном отрезке ![[a,b]](https://intuit.ru//sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) , разбивая его на
, разбивая его на  равных промежутков точками
равных промежутков точками 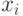 ,
,  ,
, 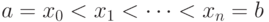 и выбирая значения
и выбирая значения  ,
,  указанным способом.
указанным способом. 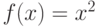 на отрезке
на отрезке ![[0,3]](https://intuit.ru//sites/default/files/tex_cache/ed9c05fe24c0f49f5d73f494a921e0c4.png) , значения
, значения 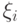 ,
, 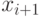 .
.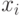 .
. на отрезке
на отрезке ![[1,6]](https://intuit.ru//sites/default/files/tex_cache/2bccbe7a6d329cdc83f6595403ff524e.png) , значения
, значения 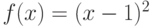 на отрезке
на отрезке ![[1,4]](https://intuit.ru//sites/default/files/tex_cache/94fe668c80113341416b96929a8f1024.png) , значения
, значения ![[-1,1]](https://intuit.ru//sites/default/files/tex_cache/d060b17b29e0dae91a1cac23ea62281a.png) , значения
, значения 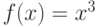 на отрезке
на отрезке ![[-2,3]](https://intuit.ru//sites/default/files/tex_cache/b0d7f8a67eadd14f5ecf59564e6b1c08.png) , значения
, значения  на отрезке
на отрезке ![[-1,4]](https://intuit.ru//sites/default/files/tex_cache/75088b46132fb25afe18309c5681c320.png) , значения
, значения ![[x_i,x_{i+1}]](https://intuit.ru//sites/default/files/tex_cache/ed75161bcea8dc1b8e616c48806cc6e7.png) .
.