При вычислении длины кривой в полярных координатах функция 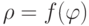 на отрезке
на отрезке ![[\alpha,\beta]](https://intuit.ru//sites/default/files/tex_cache/76ec9b92b11ea1475095ec6a47fccd53.png) должна удовлетворять условиям:
должна удовлетворять условиям:
(Отметьте один правильный вариант ответа.)
Варианты ответа
дифференцируемость
непрерывная дифференцируемость(Верный ответ)
непрерывность

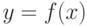 на отрезке
на отрезке ![[a,b]](https://intuit.ru//sites/default/files/tex_cache/2c3d331bc98b44e71cb2aae9edadca7e.png) должна удовлетворять условиям:
должна удовлетворять условиям: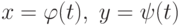 на отрезке
на отрезке ![[t_0,T]](https://intuit.ru//sites/default/files/tex_cache/71e0859cd3bff90002eb796d8f2918a0.png) должны удовлетворять условиям:
должны удовлетворять условиям: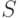 кривой
кривой 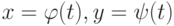 , вычисляется по формуле
, вычисляется по формуле 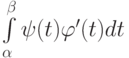 . Тогда на отрезке
. Тогда на отрезке  должны выполняться условия:
должны выполняться условия: . Отметьте верные утверждения:
. Отметьте верные утверждения: для функции
для функции  на заданном отрезке
на заданном отрезке  равных промежутков точками
равных промежутков точками 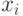 ,
,  ,
, 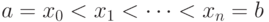 и выбирая значения
и выбирая значения  ,
,  указанным способом.
указанным способом. 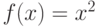 на отрезке
на отрезке ![[0,3]](https://intuit.ru//sites/default/files/tex_cache/ed9c05fe24c0f49f5d73f494a921e0c4.png) , значения
, значения 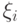 ,
, 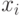 .
.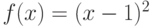 на отрезке
на отрезке ![[1,4]](https://intuit.ru//sites/default/files/tex_cache/94fe668c80113341416b96929a8f1024.png) , значения
, значения 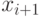 .
.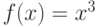 на отрезке
на отрезке ![[-2,3]](https://intuit.ru//sites/default/files/tex_cache/b0d7f8a67eadd14f5ecf59564e6b1c08.png) , значения
, значения