Заданы два уравнения кривых второго порядка:

Найти координаты точек их пересечения, если известны значения коэффициентов:
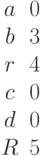
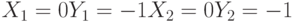
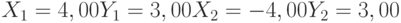
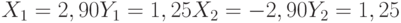

Заданы два уравнения кривых второго порядка:

Найти координаты точек их пересечения, если известны значения коэффициентов:
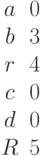
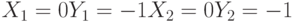
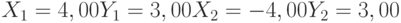
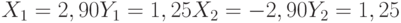
Заданы два уравнения кривых второго порядка:

Найти координаты точек их пересечения, если известны значения коэффициентов:
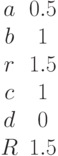
Заданы два уравнения кривых второго порядка:

Найти координаты точек их пересечения, если известны значения коэффициентов:
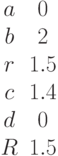
Заданы два уравнения кривых второго порядка:

Найти координаты точек их пересечения, если известны значения коэффициентов:
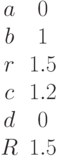
Заданы два уравнения кривых второго порядка:

Найти координаты точек их пересечения, если известны значения коэффициентов:
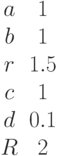
Заданы два уравнения кривых второго порядка:

Найти координаты точек их пересечения, если известны значения коэффициентов:
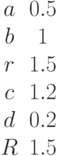
Заданы два уравнения кривых второго порядка:

Найти координаты точек их пересечения, если известны значения коэффициентов:

Заданы два уравнения кривых второго порядка:

Найти координаты точек их пересечения, если известны значения коэффициентов:
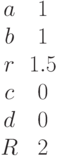
Заданы два уравнения кривых второго порядка:

Найти координаты точек их пересечения, если известны значения коэффициентов:
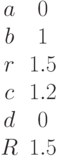
Заданы два уравнения кривых второго порядка:

Найти координаты точек их пересечения, если известны значения коэффициентов:
