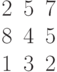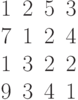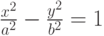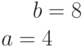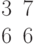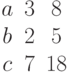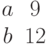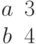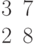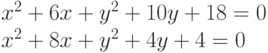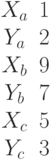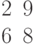Основы аналитической геометрии - ответы
Составить уравнение плоскости проходящей через прямую уравнением:
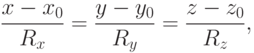
Параллельно прямой:

Уравнение представить в виде:
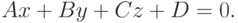

Найти координаты точки, в которой с координатной плоскостью YOZ пересекается прямая, образованная пересечением двух плоскостей, заданных уравнениями:
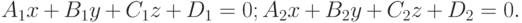
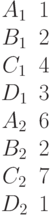
Задана матрица коэффициентов левой части системы линейных алгебраических уравнений:

И одно из базисных решений:
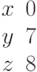
Найти методом Гаусса базисные решения.
Найти коэффициенты уравнения прямой y=kx+b по координатам двух точек, через которые проходит прямая: (3;7) и (8;3).
Даны отрезки, отсекаемые прямой на осях координат: a=1; b=-2. Найти координаты точки принадлежащей прямой: (5;…).
Задано уравнение кривой в виде: 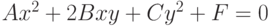 . Найти преобразование координат
. Найти преобразование координат 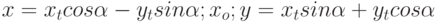 , которое приводит уравнение к виду:
, которое приводит уравнение к виду:
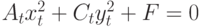 . Указать значение
. Указать значение 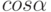 .
.
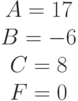
Задано параметрически уравнение эллипса:
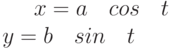
Значения  и
и 
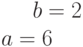
Какая из нижеприведенных точек лежит внутри этой кривой.
Составить уравнение плоскости проходящей через точку с координатами 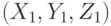 и перпендикулярную прямой заданной уравнением:
и перпендикулярную прямой заданной уравнением:
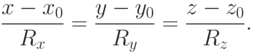
Уравнение представить в виде:
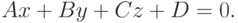

На прямой даны две точки: А(4) и В(10). Найти координаты точки М, лежащей на отрезке AB, если известно, что АМ=2МВ.
Заданы координаты точки в декартовой системе координат (6;8). Найти ее координаты в полярной системе координат. Укажите угол с точностью до одного знака после запятой.
Заданы координаты точки в декартовой системе координат (6;8;12). Найти ее координаты в цилиндрической системе координат.
Заданы координаты точки в декартовой системе координат (8,5;8,5;8,5). Найти ее координаты в сферической системе.
Заданы координаты точки в сферической системе координат:  . Найти ее координаты в декартовой системе.
. Найти ее координаты в декартовой системе.
Найти проекции на оси координат направляющего вектора прямой проходящей через две точки, координаты которых: (5;2) и (9;7).
Найти длины отрезков отсекаемых на осях координат прямой проходящей через две точки, координаты которых: (5;2) и (9;7).
Даны отрезки отсекаемые прямой на осях координат: a=2; b=7. Найти коэффициенты уравнения прямой : y=kx+b.
Через точку с координатами (6;4) проходит пряма, направляющий вектор которой равен (8;2). Найти коэффициенты уравнения этой прямой: y=kx+b.
Через точку с координатами (6;4) проходит пряма, направляющий вектор которой равен (8;2). Найти отрезки, отсекаемые этой прямой на осях координат.
Задана матрица коэффициентов левой части системы линейных алгебраических уравнений:
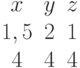
И столбец свободных членов:
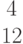
Найти методом Гаусса базисные решения.
Задана матрица коэффициентов левой части системы линейных алгебраических уравнений:

И одно из базисных решений:

Найти методом Гаусса базисные решения.
Задана матрица коэффициентов левой части системы линейных алгебраических уравнений:
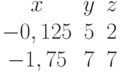
И одно из базисных решений:
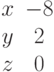
Найти методом Гаусса базисные решения.
Задана матрица коэффициентов левой части системы линейных алгебраических уравнений:
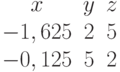
И одно из базисных решений:
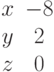
Найти методом Гаусса базисные решения.
Область поиска решения задачи линейного программирования имеет вид выпуклого многоугольника с вершинами:
 | 20 | 0 | 0 | 10 |
 | 0 | 0 | 30 | 18 |
Целевая функция имеет вид.
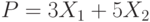
В какой вершине целевая функция достигает максимального значения.
Даны матрица левой части и столбец свободных членов системы линейных алгебраических уравнений.

Найти решение методом Крамера.
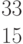
Заданы координаты точки (6;9) . Найдите координаты после трансляции системы координат вдоль оси ОХ на a=5.
Заданы координаты точки (3;4). Найдите координаты после трансляции системы координат вдоль оси ОУ на b=7.
Заданы координаты точки (8;7). Найдите координаты после трансляции системы координат вдоль оси ОХ на a= 4 и вдоль оси ОУ на b=2.
Заданы координаты точки (6;9). Найдите координаты после трансляции системы координат вдоль оси ОХ на a= 4 и поворота против часовой стрелки на 30 градусов.
Заданы координаты точки (3;4). Найдите координаты после трансляции системы координат вдоль оси ОУ на b= 7 и поворота против часовой стрелки на 30 градусов.
Заданы координаты точки (3;4). Найдите координаты после трансляции системы координат вдоль оси ОХ на a= 5; вдоль оси ОУ на b= 4 и поворота против часовой стрелки на 30 градусов.
После трансляции координаты точки приняли значение (6;9). Найдите координаты до трансляции системы координат вдоль оси ОХ на a=5; вдоль оси ОУ на b=4.
После трансляции координаты точки приняли значение (6;9). Найдите координаты до трансляции системы координат вдоль оси ОХ на a= 5; вдоль оси ОУ на b= 4 и повороте против часовой стрелки на 30 градусов.
Условия.
Заданы два уравнения кривых второго порядка:

Найти координаты точек их пересечения, если известны значения коэффициентов:

Заданы два уравнения кривых второго порядка:

Найти координаты точек их пересечения, если известны значения коэффициентов:
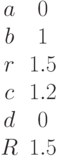
Заданы два уравнения кривых второго порядка:

Найти координаты точек их пересечения, если известны значения коэффициентов:
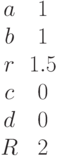
Заданы два уравнения кривых второго порядка:

Найти координаты точек их пересечения, если известны значения коэффициентов:

Заданы два уравнения кривых второго порядка:

Найти координаты точек их пересечения, если известны значения коэффициентов:

Заданы два уравнения кривых второго порядка:

Найти координаты точек их пересечения, если известны значения коэффициентов:
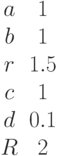
Заданы два уравнения кривых второго порядка:

Найти координаты точек их пересечения, если известны значения коэффициентов:
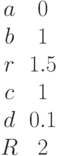
Заданы два уравнения кривых второго порядка:

Найти координаты точек их пересечения, если известны значения коэффициентов:
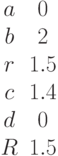
Условия.
Задано уравнение прямой в виде:  . Укажите, какое из уравнений вида:
. Укажите, какое из уравнений вида: 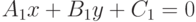 ; соответствует прямой перпендикулярной прямой заданной уравнением
; соответствует прямой перпендикулярной прямой заданной уравнением  . Считать, что
. Считать, что
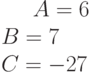
Задано уравнение прямой в виде:  . Укажите, какое из уравнений вида:
. Укажите, какое из уравнений вида: 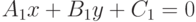 ; соответствует прямой параллельной прямой заданной уравнением
; соответствует прямой параллельной прямой заданной уравнением 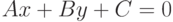 , и проходящей через точку
, и проходящей через точку 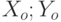 . Считать, что
. Считать, что


Задано уравнение прямой в виде:  . Укажите, какое из уравнений вида:
. Укажите, какое из уравнений вида: 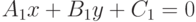 ; соответствует прямой перпендикулярной прямой заданной уравнением
; соответствует прямой перпендикулярной прямой заданной уравнением 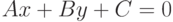 , и проходящей через точку
, и проходящей через точку 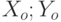 . Считать, что
. Считать, что


Задано уравнение прямой в виде:  . Найдите координаты точки пересечения с этой прямой перпендикуляра к ней проходящего через точку
. Найдите координаты точки пересечения с этой прямой перпендикуляра к ней проходящего через точку 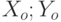 . Считать, что
. Считать, что

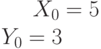
Найти отрезки, отсекаемые на осях координат (a на оси ОХ и b на оси OY) прямой проходящей через точку с координатами 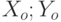 , если известно, что
, если известно, что 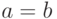 .
.
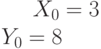
Найти отрезки, отсекаемые на осях координат (a на оси ОХ и b на оси OY) прямой проходящей через точку с координатами 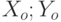 , если известно, что
, если известно, что 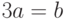 .
.
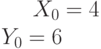
Найти отрезки, отсекаемые на осях координат (a на оси ОХ и b на оси OY) прямой проходящей через точку с координатами 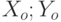 , если известно, что
, если известно, что 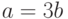 .
.
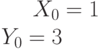
Заданы уравнения двух пересекающихся прямых:

Найти уравнения биссектрис углов образованных этими прямыми:

Известно, что:
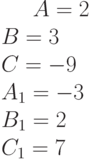
Задано параметрически уравнение эллипса:
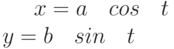
Значения  и
и 
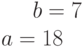
Какая из нижеприведенных точек лежит внутри этой кривой.
Задано параметрически уравнение эллипса:
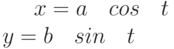
Значения  и
и 
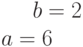
Какая из нижеприведенных точек лежит на этой кривой.
Задано параметрически уравнение эллипса:
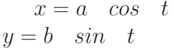
Значения  и
и 
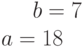
Какая из нижеприведенных точек лежит внутри этой кривой.
Задано уравнение кривой в виде: 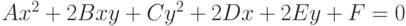 . Найти преобразование координат
. Найти преобразование координат 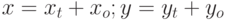 , при котором уравнение принимает вид:
, при котором уравнение принимает вид:
 . Указать значение
. Указать значение 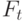 .
.
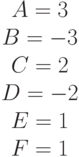
Задано уравнение кривой в виде: 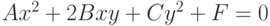 . Найти преобразование координат
. Найти преобразование координат  , которое приводит уравнение к виду:
, которое приводит уравнение к виду:
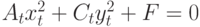 . Указать значение
. Указать значение  .
.

Задано уравнение кривой в виде: 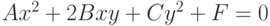 . Найти преобразование координат
. Найти преобразование координат  , которое приводит уравнение к виду:
, которое приводит уравнение к виду:
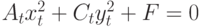 . Указать значение
. Указать значение  в градусах.
в градусах.

Задано уравнение кривой в виде: 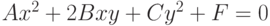 . Найти преобразование координат
. Найти преобразование координат 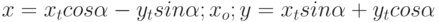 , которое приводит уравнение к виду:
, которое приводит уравнение к виду:
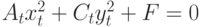 . Указать значение
. Указать значение 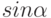 .
.

Задано уравнение кривой в виде: Ax2+2Bxy+Cy2+F=0. Найти преобразование координат 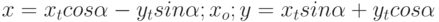 , которое приводит уравнение к виду:
, которое приводит уравнение к виду:
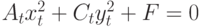 . Указать значение
. Указать значение 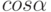 .
.

Найти уравнение плоскости в виде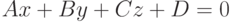 , если известны координаты точки и двух векторов лежащих в этой плоскости.
, если известны координаты точки и двух векторов лежащих в этой плоскости.
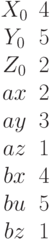
Найти уравнение плоскости в отрезках, если известны координаты точки и двух векторов лежащих в этой плоскости.
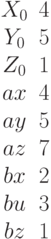
Задано уравнение плоскости в виде 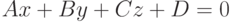 . Найти значения направляющих косинусов нормального вектора этой плоскости.
. Найти значения направляющих косинусов нормального вектора этой плоскости.
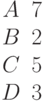
Задано уравнение плоскости в виде 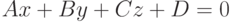 . Найти значения углов (в градусах) между нормальным вектором этой плоскости и координатными осями.
. Найти значения углов (в градусах) между нормальным вектором этой плоскости и координатными осями.
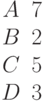
Найти проекции направляющего вектора прямой образованной пересечением двух плоскостей, заданных уравнениями:
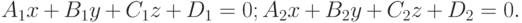
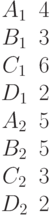
Найти угол, под которым с плоскостью
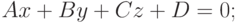
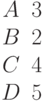
пересекается прямая, образованная пересечением двух плоскостей, заданных уравнениями:
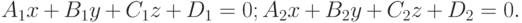

Найти координаты точки, в которой с координатной плоскостью YOZ пересекается прямая, образованная пересечением двух плоскостей, заданных уравнениями:
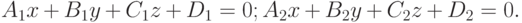

Найти координаты точки, в которой с координатной плоскостью ZOX пересекается прямая, образованная пересечением двух плоскостей, заданных уравнениями:
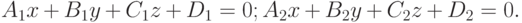

Найти координаты точки, в которой с координатной плоскостью XOY пересекается прямая, образованная пересечением двух плоскостей, заданных уравнениями:
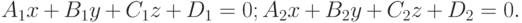
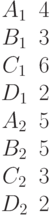
Составить уравнение плоскости проходящей через точку с координатами
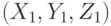 и прямую заданную уравнением:
и прямую заданную уравнением:
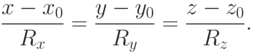
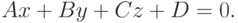

Составить уравнение плоскости проходящей через прямую уравнением:
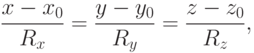
Параллельно прямой:

Уравнение представить в виде:
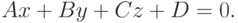

Составить уравнение плоскости проходящей через точку с координатами 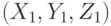 и перпендикулярную прямой заданной уравнением:
и перпендикулярную прямой заданной уравнением:
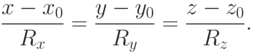
Уравнение представить в виде:
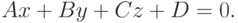
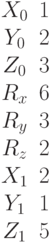
Укажите уравнение прямой, лежащей в одной плоскости с прямой, заданной уравнением:
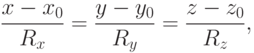
Уравнение прямой представить в виде:


Составить уравнение плоскости проходящей через прямую, заданную уравнением:
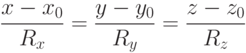
перпендикулярно плоскости:
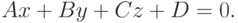
Уравнение представить в виде:


Укажите проекции направляющего вектора прямой, проходящей через точку 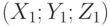 перпендикулярно к прямой заданной уравнением:
перпендикулярно к прямой заданной уравнением:
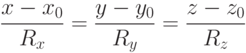
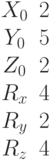
Дан однополостный гиперболоид. Его полуоси a, b, c. Выясните, какая из точек принадлежит однополосному гиперболоиду.
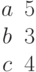
Дан двухполостный гиперболоид. Его полуоси a, b, c. Выясните, какая из точек принадлежит двухполосному гиперболоиду.
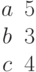
Найти точки пересечения прямой, проходящей через точку с координатами (Xo,Yo,Zo) в направлении вектора (Rx,Ry,Rz), с поверхностью заданной уравнением:

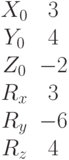
Найти точки пересечения прямой, проходящей через точку с координатами (Xo,Yo,Zo) в направлении вектора (Rx,Ry,Rz), с поверхностью заданной уравнением:


Найти точки пересечения прямой, проходящей через точку с координатами (Xo,Yo,Zo) в направлении вектора (Rx,Ry,Rz), с поверхностью заданной уравнением:


Дана расширенная матрица системы линейных алгебраических уравнений. Найти значения вспомогательных определителей.

Заданы два уравнения кривых второго порядка:

Найти координаты точек их пересечения, если известны значения коэффициентов:
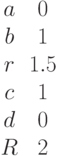
Найти угол, под которым с плоскостью
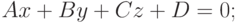
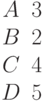
пересекается прямая, образованная пересечением двух плоскостей, заданных уравнениями:
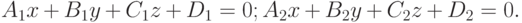
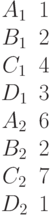
Задано уравнение плоскости в виде 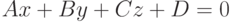 . Найти значения углов (в градусах) между нормальным вектором этой плоскости и координатными осями.
. Найти значения углов (в градусах) между нормальным вектором этой плоскости и координатными осями.
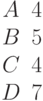
Задана матрица коэффициентов левой части системы линейных алгебраических уравнений:
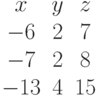
И одно из базисных решений:
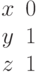
Найти методом Гаусса базисные решения.
Задано уравнение кривой в виде: 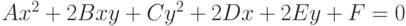 . Найти преобразование координат
. Найти преобразование координат 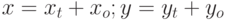 , при котором уравнение принимает вид:
, при котором уравнение принимает вид:
 . Указать значение
. Указать значение 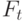 .
.

Условия.
Заданы два уравнения кривых второго порядка:

Найти координаты точек их пересечения, если известны значения коэффициентов:
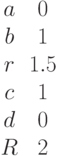
Заданы координаты точки (8;7) . Найдите координаты после трансляции системы координат вдоль оси ОХ на a=5.
Даны полуоси гиперболы  и
и  . Найти расстояние между ее директрисами.
. Найти расстояние между ее директрисами.
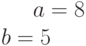 Ответ введите с точностью до 2-го знака после запятой.
Ответ введите с точностью до 2-го знака после запятой.
Даны матрица левой части и столбец свободных членов системы линейных алгебраических уравнений.
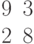
Найти главный определитель системы.
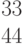
Дана матрица левой части и столбец свободных членов системы линейных алгебраических уравнений.

Вычислить первый вспомогательный определитель системы.

Даны полуоси эллипса  и
и  . Найти расстояние между его директрисами.
. Найти расстояние между его директрисами.
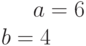 Ответ введите с точностью до 2-го знака после запятой.
Ответ введите с точностью до 2-го знака после запятой.
Даны полуоси эллипса  и
и  . Найти его эксцентриситет.
. Найти его эксцентриситет.
 Ответ введите с точностью до 2-го знака после запятой.
Ответ введите с точностью до 2-го знака после запятой.
Дана матрица левой части и столбец свободных членов системы линейных алгебраических уравнений.
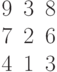
Вычислить главный определитель системы.

Заданы уравнения прямых в виде  и
и 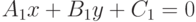 .
.
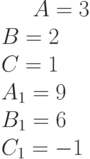
Найти расстояние между прямыми.
Ответ введите с точностью до 2-го знака после запятой.Область поиска решения задачи линейного программирования имеет вид выпуклого многоугольника с вершинами:
 | 20 | 0 | 0 | 10 |
 | 0 | 0 | 30 | 18 |
Целевая функция имеет вид.
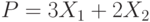
Даны матрица левой части и столбец свободных членов системы линейных алгебраических уравнений.
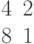
Найти главный определитель системы.
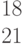
Даны матрица левой части и столбец свободных членов системы линейных алгебраических уравнений.
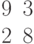
Найти первый вспомогательный определитель системы.
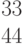
Даны матрица левой части и столбец свободных членов системы линейных алгебраических уравнений.
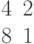
Найти второй вспомогательный определитель системы.
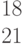
Дана матрица левой части и столбец свободных членов системы линейных алгебраических уравнений.
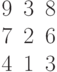
Вычислить первый вспомогательный определитель системы.

Дана матрица левой части и столбец свободных членов системы линейных алгебраических уравнений.
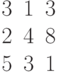
Вычислить второй вспомогательный определитель системы.
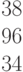
Дана матрица левой части и столбец свободных членов системы линейных алгебраических уравнений.

Вычислить третий вспомогательный определитель системы.

Задано уравнение прямой в виде  .
.
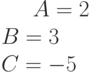
Найти угол в градусах между прямой и направлением оси ОХ.
Ответ введите с точностью до 1-го знака после запятой.Задано уравнение прямой в виде  .
.
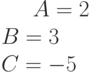
Найти расстояние от прямой до начала координат.
Ответ введите с точностью до 2-го знака после запятой.Заданы уравнения прямых в виде  и
и 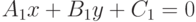 .
.

Найти угол между прямыми (в градусах).
Ответ введите с точностью до 1-го знака после запятой.Заданы уравнения прямых в виде  и
и 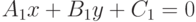 .
.

Найти расстояние между прямыми.
Ответ введите с точностью до 2-го знака после запятой.Задано уравнение прямой в виде  .
.
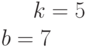
Найти угол в градусах между прямой и направлением оси ОХ.
Ответ введите с точностью до 1-го знака после запятой.Задано уравнение прямой в виде  .
.
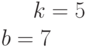
Расстояние между прямой и началом координат. Ответ введите с точностью до 2-го знака после запятой.
Заданы уравнения двух прямых в виде  и
и  .
.

Угол (в градусах) между прямыми.
Ответ введите с точностью до 1-го знака после запятой.Даны полуоси эллипса.  и
и  . Найти расстояние между его фокусами.
. Найти расстояние между его фокусами.
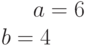 Ответ введите с точностью до 2-го знака после запятой.
Ответ введите с точностью до 2-го знака после запятой.
Даны полуоси гиперболы.  и
и  . Найти расстояние между ее фокусами.
. Найти расстояние между ее фокусами.
 Ответ введите с точностью до 2-го знака после запятой.
Ответ введите с точностью до 2-го знака после запятой.
Даны полуоси эллипса  и
и  . Найти его эксцентриситет.
. Найти его эксцентриситет.
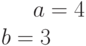 Ответ введите с точностью до 2-го знака после запятой.
Ответ введите с точностью до 2-го знака после запятой.
Даны полуоси гиперболы  и
и  . Найти ее эксцентриситет.
. Найти ее эксцентриситет.
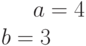 Ответ введите с точностью до 2-го знака после запятой.
Ответ введите с точностью до 2-го знака после запятой.
Даны полуоси эллипса  и
и  . Найти расстояние между его директрисами.
. Найти расстояние между его директрисами.
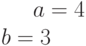 Ответ введите с точностью до 2-го знака после запятой.
Ответ введите с точностью до 2-го знака после запятой.
Даны полуоси гиперболы  и
и  . Найти расстояние между ее директрисами.
. Найти расстояние между ее директрисами.
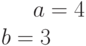 Ответ введите с точностью до 1-го знака после запятой.
Ответ введите с точностью до 1-го знака после запятой.
Даны полуоси гиперболы  и
и  . Найти значение коэффициента
. Найти значение коэффициента  в ее уравнении в полярной системе координат. Ответ введите с точностью до 3-го знака после запятой.
в ее уравнении в полярной системе координат. Ответ введите с точностью до 3-го знака после запятой.
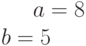
Задано уравнение кривой в виде: 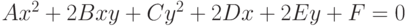 . Найти преобразование координат
. Найти преобразование координат 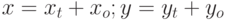 , при котором уравнение принимает вид:
, при котором уравнение принимает вид:
 . Указать значение
. Указать значение 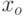 .
.

Задано уравнение кривой в виде: 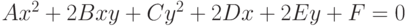 . Найти преобразование координат
. Найти преобразование координат 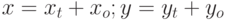 , при котором уравнение принимает вид:
, при котором уравнение принимает вид:
 . Указать значение
. Указать значение 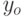 .
.

Найти расстояние от точки (1;2;4) до плоскости, если известны координаты точки и двух векторов лежащих в этой плоскости. Ответ введите с точностью до 2-го знака после запятой.
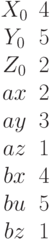
Найти угол между плоскостью заданной уравнением 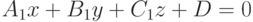 и плоскостью, если известны координаты точки и двух векторов лежащих в этой плоскости. Ответ введите с точностью до 1-го знака после запятой.
и плоскостью, если известны координаты точки и двух векторов лежащих в этой плоскости. Ответ введите с точностью до 1-го знака после запятой.
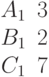

Найти расстояние от точки (1;2;4) до плоскости, если известны координаты трех точек лежащих в этой плоскости.

Найти угол между плоскостью заданной уравнением 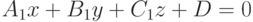 и плоскостью, если известны координаты трех точек лежащих в этой плоскости. Ответ введите в градусах с точностью до 1-го знака после запятой.
и плоскостью, если известны координаты трех точек лежащих в этой плоскости. Ответ введите в градусах с точностью до 1-го знака после запятой.
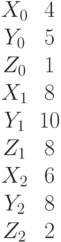
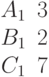
Задано уравнение плоскости в виде 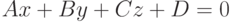 . Найти расстояние до плоскости от начала координат. Ответ введите с точностью до 3-го знака после запятой.
. Найти расстояние до плоскости от начала координат. Ответ введите с точностью до 3-го знака после запятой.
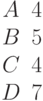
Задано уравнение плоскости в виде 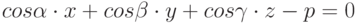 . Найти значение недостающего косинуса. Ответ введите с точностью до 3-го знака после запятой.
. Найти значение недостающего косинуса. Ответ введите с точностью до 3-го знака после запятой.
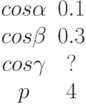
Задано уравнение плоскости в виде 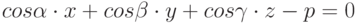 . Найти значение недостающего косинуса. Ответ введите с точностью до 3-го знака после запятой.
. Найти значение недостающего косинуса. Ответ введите с точностью до 3-го знака после запятой.

Задано уравнение плоскости в виде 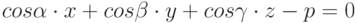 . Найти значение недостающего косинуса. Ответ введите с точностью до 3-го знака после запятой.
. Найти значение недостающего косинуса. Ответ введите с точностью до 3-го знака после запятой.

Задано уравнение плоскости в виде 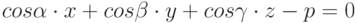 . Найти расстояние до этой плоскости от точки с координатами (1;2;3). Ответ введите с точностью до 2-го знака после запятой.
. Найти расстояние до этой плоскости от точки с координатами (1;2;3). Ответ введите с точностью до 2-го знака после запятой.
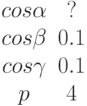
Найти угол (в градусах), под которым с координатной плоскостью YOZ пересекается прямая, образованная пересечением двух плоскостей, заданных уравнениями:
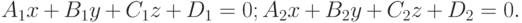
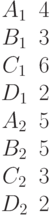
Найти угол (в градусах), под которым с координатной плоскостью ZOX пересекается прямая, образованная пересечением двух плоскостей, заданных уравнениями:
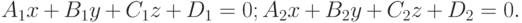
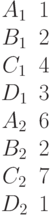
Найти угол (в градусах), под которым с координатной плоскостью XOY пересекается прямая, образованная пересечением двух плоскостей, заданных уравнениями:
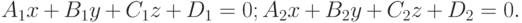
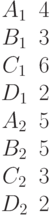
Найти кратчайшее расстояние от точки 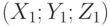 до прямой:
до прямой:
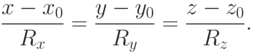
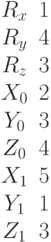
Найдите кратчайшее расстояние между двумя прямыми:

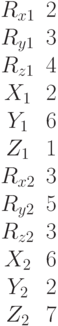
Определите, сколько общих точек имеет окружность радиуса R с центром в начале координат с прямой заданной уравнением 

Определите, сколько общих точек имеет окружность радиуса R с центром в точке координатами (Xo;Yo) с прямой заданной уравнением  .
.
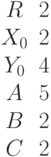
Определите, сколько общих точек имеет эллипс с посуосями a и b и центром в начале координат с прямой заданной уравнением  .
.

Определите, сколько общих точек имеет эллипс с посуосями a и b и центром в точке с координатами Xo, Yo с прямой заданной уравнением  .
.

Даны полуоси эллипса  и
и  . Найти его эксцентриситет.
. Найти его эксцентриситет.
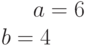 Ответ введите с точностью до 2-го знака после запятой.
Ответ введите с точностью до 2-го знака после запятой.
Найти угол (в градусах), под которым с координатной плоскостью XOY пересекается прямая, образованная пересечением двух плоскостей, заданных уравнениями:
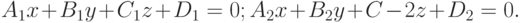

После трансляции координаты точки приняли значение (3;4). Найдите координаты до трансляции системы координат вдоль оси ОХ на a= 5; вдоль оси ОУ на b= 4.
Составить уравнение плоскости проходящей через прямую, заданную уравнением:
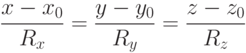
перпендикулярно плоскости:
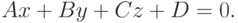
Уравнение представить в виде:
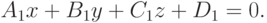
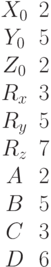
Условия.
Задано уравнение кривой в виде: 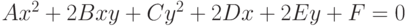 . Найти преобразование координат
. Найти преобразование координат 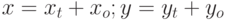 , при котором уравнение принимает вид:
, при котором уравнение принимает вид:
 . Указать значение
. Указать значение 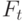 .
.

Задано уравнение плоскости в виде 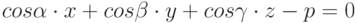 . Найти значение недостающего косинуса. Ответ введите с точностью до 3-го знака после запятой.
. Найти значение недостающего косинуса. Ответ введите с точностью до 3-го знака после запятой.

Даны полуоси гиперболы  и
и  . Найти значение коэффициента
. Найти значение коэффициента  в ее уравнении в полярной системе координат. Ответ введите с точностью до 2-го знака после запятой.
в ее уравнении в полярной системе координат. Ответ введите с точностью до 2-го знака после запятой.
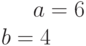
Укажите уравнение прямой, лежащей в одной плоскости с прямой, заданной уравнением:
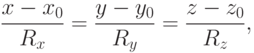
Уравнение прямой представить в виде:

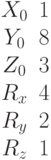
Дана матрица левой части и столбец свободных членов системы линейных алгебраических уравнений.

Вычислить второй вспомогательный определитель системы.

Задано уравнение плоскости в виде 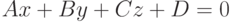 . Найти значения направляющих косинусов нормального вектора этой плоскости.
. Найти значения направляющих косинусов нормального вектора этой плоскости.
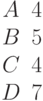
Заданы координаты точки в декартовой системе координат (8;6). Найти ее координаты в полярной системе координат. В качестве ответа введите угол, округлив его до целого.
Заданы координаты точки в декартовой системе координат (8;6;12). Найти ее координаты в цилиндрической системе координат.
Найти коэффициенты уравнения прямой y=kx+b по координатам двух точек, через которые проходит прямая: (4;6) и (5;9).
Найти проекции на оси координат направляющего вектора прямой проходящей через две точки, координаты которых: (3;7) и (8;3).
Даны отрезки отсекаемые прямой на осях координат: a=1; b=-2. Найти коэффициенты уравнения прямой : y=kx+b.
Даны отрезки, отсекаемые прямой на осях координат: a=4; b=4. Найти координаты точки принадлежащей прямой: (5;…).
Через точку с координатами (3;12) проходит пряма, направляющий вектор которой равен (2;7). Найти коэффициенты уравнения этой прямой: y=kx+b.
Через точку с координатами (3;9) проходит пряма, направляющий вектор которой равен (5;4). Найти отрезки, отсекаемые этой прямой на осях координат.
Задана матрица коэффициентов левой части системы линейных алгебраических уравнений:

И столбец свободных членов:

Найти методом Гаусса базисные решения.
Задана матрица коэффициентов левой части системы линейных алгебраических уравнений:

И одно из базисных решений:
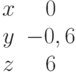
Найти методом Гаусса базисные решения.
Задана матрица коэффициентов левой части системы линейных алгебраических уравнений:
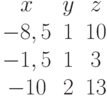
И одно из базисных решений:
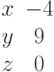
Найти методом Гаусса базисные решения.
Задана матрица коэффициентов левой части системы линейных алгебраических уравнений:
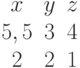
И одно из базисных решений:
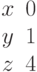
Найти методом Гаусса базисные решения.
Область поиска решения задачи линейного программирования имеет вид выпуклого многоугольника с вершинами:
 | 20 | 0 | 0 | 10 |
 | 0 | 0 | 30 | 18 |
Целевая функция имеет вид.
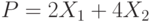
Найти максимальное значение целевой функции.
Область поиска решения задачи линейного программирования имеет вид выпуклого многоугольника с вершинами:
 | 20 | 0 | 0 | 10 |
 | 0 | 0 | 30 | 18 |
Целевая функция имеет вид.
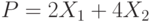
В какой вершине целевая функция достигает максимального значения.
Даны матрица левой части и столбец свободных членов системы линейных алгебраических уравнений.

Найти главный определитель системы.
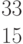
Даны матрица левой части и столбец свободных членов системы линейных алгебраических уравнений.
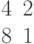
Найти первый вспомогательный определитель системы.
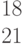
Дана матрица левой части и столбец свободных членов системы линейных алгебраических уравнений.

Вычислить главный определитель системы.

Дана матрица левой части и столбец свободных членов системы линейных алгебраических уравнений.

Вычислить второй вспомогательный определитель системы.

Даны два вектора.
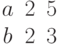
Найти угол между ними (в градусах).
Ответ введите с точностью до 1-го знака после запятой.Заданы координаты точки (3;4). Найдите координаты после трансляции системы координат вдоль оси ОХ на a=5.
Заданы координаты точки (8;7). Найдите координаты после трансляции системы координат вдоль оси ОУ на b=7.
Заданы координаты точки (8;7). Найдите координаты после трансляции системы координат вдоль оси ОХ на a= 4 и поворота против часовой стрелки на 30 градусов.
Заданы координаты точки (6;9). Найдите координаты после трансляции системы координат вдоль оси ОУ на b= 7 и поворота против часовой стрелки на 30 градусов.
После трансляции координаты точки приняли значение (8;7). Найдите координаты до трансляции системы координат вдоль оси ОХ на a= 5; вдоль оси ОУ на b= 4 и повороте против часовой стрелки на 30 градусов.
Заданы два уравнения кривых второго порядка:

Найти координаты точек их пересечения, если известны значения коэффициентов:
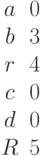
Заданы два уравнения кривых второго порядка:

Найти координаты точек их пересечения, если известны значения коэффициентов:
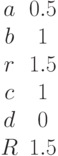
Заданы два уравнения кривых второго порядка:

Найти координаты точек их пересечения, если известны значения коэффициентов:
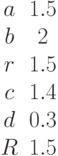
Заданы два уравнения кривых второго порядка:

Найти координаты точек их пересечения, если известны значения коэффициентов:
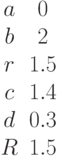
Заданы уравнения прямых в виде  и
и 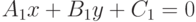 .
.
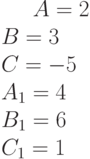
Найти расстояние между прямыми. Ответ округлить до второй цифры после запятой.
Задано уравнение прямой в виде  .
.
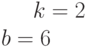
Расстояние между прямой и началом координат.
Ответ введите с точностью до 2-го знака после запятой.Заданы уравнения двух прямых в виде  и
и  .
.

Угол (в градусах) между прямыми. Ответ введите с точностью до 1-го знака после запятой.
Задано уравнение прямой в виде:  . Укажите, какое из уравнений вида:
. Укажите, какое из уравнений вида:  ; соответствует прямой перпендикулярной прямой заданной уравнением
; соответствует прямой перпендикулярной прямой заданной уравнением 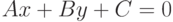 . Считать, что
. Считать, что

Задано уравнение прямой в виде:  . Укажите, какое из уравнений вида:
. Укажите, какое из уравнений вида: 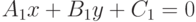 ; соответствует прямой параллельной прямой заданной уравнением
; соответствует прямой параллельной прямой заданной уравнением 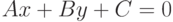 , и проходящей через точку
, и проходящей через точку 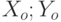 . Считать, что
. Считать, что

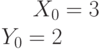
Задано уравнение прямой в виде:  . Укажите, какое из уравнений вида:
. Укажите, какое из уравнений вида: 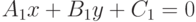 ; соответствует прямой перпендикулярной прямой заданной уравнением
; соответствует прямой перпендикулярной прямой заданной уравнением 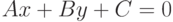 , и проходящей через точку
, и проходящей через точку 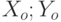 . Считать, что
. Считать, что

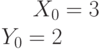
Задано уравнение прямой в виде:  . Найдите координаты точки пересечения с этой прямой перпендикуляра к ней проходящего через точку
. Найдите координаты точки пересечения с этой прямой перпендикуляра к ней проходящего через точку 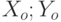 . Считать, что
. Считать, что

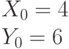
Найти отрезки, отсекаемые на осях координат (a на оси ОХ и b на оси OY) прямой проходящей через точку с координатами 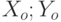 , если известно, что
, если известно, что 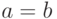 .
.
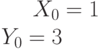
Задано параметрически уравнение эллипса:
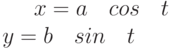
Значения  и
и 
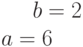
Какая из нижеприведенных точек лежит вне этой кривой.
Даны полуоси эллипса.  и
и  . Найти расстояние между его фокусами.
. Найти расстояние между его фокусами.
 Ответ введите с точностью до 2-го знака после запятой.
Ответ введите с точностью до 2-го знака после запятой.
Даны полуоси гиперболы  и
и  . Найти ее эксцентриситет.
. Найти ее эксцентриситет.
 Ответ введите с точностью до 2-го знака после запятой.
Ответ введите с точностью до 2-го знака после запятой.
Даны полуоси гиперболы  и
и  . Найти расстояние между ее директрисами.
. Найти расстояние между ее директрисами.
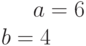 Ответ введите с точностью до 2-го знака после запятой.
Ответ введите с точностью до 2-го знака после запятой.
Задано уравнение кривой в виде: 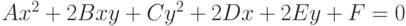 . Найти преобразование координат
. Найти преобразование координат 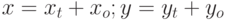 , при котором уравнение принимает вид:
, при котором уравнение принимает вид:
 . Указать значение
. Указать значение 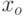 .
.
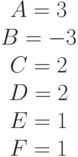
Ответ введите с точностью 2 знака после запятой.
Задано уравнение кривой в виде: 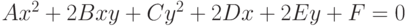 . Найти преобразование координат
. Найти преобразование координат 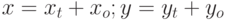 , при котором уравнение принимает вид:
, при котором уравнение принимает вид:
 . Указать значение
. Указать значение 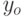 .
.
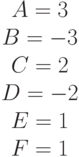
Задано уравнение кривой в виде: 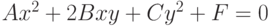 . Найти преобразование координат
. Найти преобразование координат 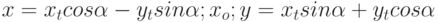 , которое приводит уравнение к виду:
, которое приводит уравнение к виду:
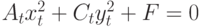 . Указать значение
. Указать значение  .
.

Задано уравнение кривой в виде: 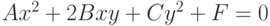 . Найти преобразование координат
. Найти преобразование координат 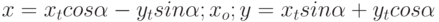 , которое приводит уравнение к виду:
, которое приводит уравнение к виду:
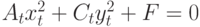 . Указать значение
. Указать значение  в градусах.
в градусах.
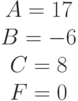
Задано уравнение кривой в виде: 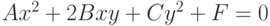 . Найти преобразование координат
. Найти преобразование координат  которое приводит уравнение к виду:
которое приводит уравнение к виду:
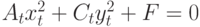 . Указать значение
. Указать значение 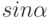 .
.

Найти уравнение плоскости в отрезках, если известны координаты точки и двух векторов лежащих в этой плоскости.
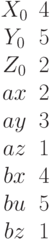
Найти расстояние от точки (1;2;4) до плоскости, если известны координаты точки и двух векторов лежащих в этой плоскости. Ответ введите с точностью до 2-го знака после запятой.
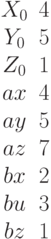
Найти острый угол между плоскостью заданной уравнением 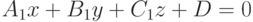 и плоскостью, если известны координаты точки и двух векторов лежащих в этой плоскости. Ответ в градусах введите с точностью до 1-го знака после запятой.
и плоскостью, если известны координаты точки и двух векторов лежащих в этой плоскости. Ответ в градусах введите с точностью до 1-го знака после запятой.
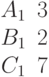
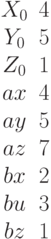
Найти расстояние от точки (1;2;4) до плоскости, если известны координаты трех точек лежащих в этой плоскости.
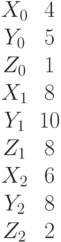
Найти острый угол между плоскостью заданной уравнением 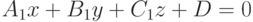 и плоскостью, если известны координаты трех точек лежащих в этой плоскости. Ответ введите с точностью до 1-го знака после запятой.
и плоскостью, если известны координаты трех точек лежащих в этой плоскости. Ответ введите с точностью до 1-го знака после запятой.

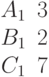
Задано уравнение плоскости в виде  . Найти значение недостающего косинуса. Ответ введите с точностью до 3-го знака после запятой.
. Найти значение недостающего косинуса. Ответ введите с точностью до 3-го знака после запятой.

Задано уравнение плоскости в виде  . Найти значение недостающего косинуса. Ответ введите с точностью до 3-го знака после запятой.
. Найти значение недостающего косинуса. Ответ введите с точностью до 3-го знака после запятой.

Задано уравнение плоскости в виде 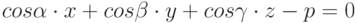 . Найти расстояние до этой плоскости от точки с координатами (1;2;3). Ответ введите с точностью до 2-го знака после запятой.
. Найти расстояние до этой плоскости от точки с координатами (1;2;3). Ответ введите с точностью до 2-го знака после запятой.

Найти проекции направляющего вектора прямой образованной пересечением двух плоскостей, заданных уравнениями:
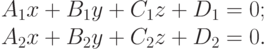
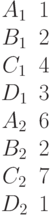
Найти угол (в градусах), под которым с координатной плоскостью YOZ пересекается прямая, образованная пересечением двух плоскостей, заданных уравнениями:
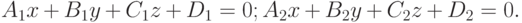
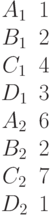
Найти координаты точки, в которой с координатной плоскостью ZOX пересекается прямая, образованная пересечением двух плоскостей, заданных уравнениями:
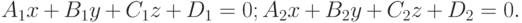
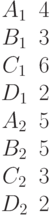
Составить уравнение плоскости проходящей через точку с координатами 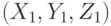 и перпендикулярную прямой заданной уравнением:
и перпендикулярную прямой заданной уравнением:
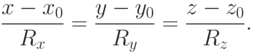
Уравнение представить в виде:
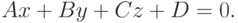
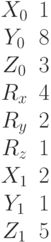
Укажите уравнение прямой, лежащей в одной плоскости с прямой, заданной уравнением:
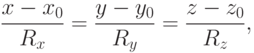
Уравнение прямой представить в виде:

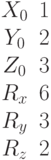
Укажите проекции направляющего вектора прямой, проходящей через точку 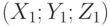 перпендикулярно к прямой заданной уравнением:
перпендикулярно к прямой заданной уравнением:
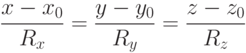
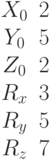
Найдите кратчайшее расстояние между двумя прямыми:

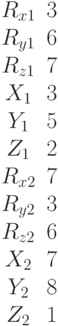
Найти точки пересечения прямой, проходящей через точку с координатами (Xo,Yo,Zo) в направлении вектора (Rx,Ry,Rz), с поверхностью заданной уравнением:
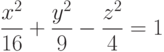

Найти точки пересечения прямой, проходящей через точку с координатами (Xo,Yo,Zo) в направлении вектора (Rx,Ry,Rz), с поверхностью заданной уравнением:
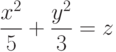

Определите, сколько общих точек имеет окружность радиуса R с центром в начале координат с прямой заданной уравнением 
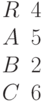
Определите, сколько общих точек имеет эллипс с посуосями a и b и центром в начале координат с прямой заданной уравнением  .
.
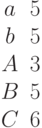
Найти угол (в градусах), под которым с координатной плоскостью XOY пересекается прямая, образованная пересечением двух плоскостей, заданных уравнениями:
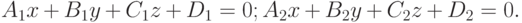
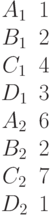
После трансляции координаты точки приняли значение (8;7). Найдите координаты до трансляции системы координат вдоль оси ОХ на a= 5; вдоль оси ОУ на b= 4.
Заданы координаты точки (8;7). Найдите координаты после трансляции системы координат вдоль оси ОУ на b= 7 и поворота против часовой стрелки на 30 градусов.
Заданы координаты точки в декартовой системе координат (3;4). Найти ее координаты в полярной системе координат.
Составить уравнение плоскости проходящей через точку с координатами 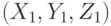 и прямую заданную уравнением:
и прямую заданную уравнением:
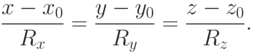
Уравнение представить в виде:
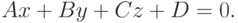

Задано уравнение прямой в виде: 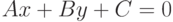 . Найдите координаты точки пересечения с этой прямой перпендикуляра к ней проходящего через точку
. Найдите координаты точки пересечения с этой прямой перпендикуляра к ней проходящего через точку 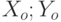 . Считать, что
. Считать, что

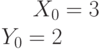
Заданы два уравнения кривых второго порядка:

Найти координаты точек их пересечения, если известны значения коэффициентов:
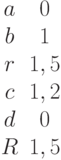
Найдите кратчайшее расстояние между двумя прямыми:

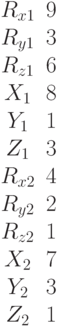
Заданы координаты точки (3;4). Найдите координаты после трансляции системы координат вдоль оси ОХ на a= 4 и вдоль оси ОУ на b=2.
Заданы уравнения двух прямых в виде  и
и  .
.
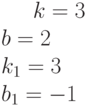
Найти расстояние между прямыми.
Ответ введите с точностью до 2-го знака после запятой.Задано параметрически уравнение эллипса:
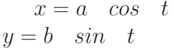
Значения  и
и 
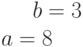
Какая из нижеприведенных точек лежит внутри этой кривой.
Задано уравнение прямой в виде  .
.

Найти расстояние от прямой до начала координат. Ответ введите с точностью до 2-го знака после запятой.
Заданы координаты точки в декартовой системе координат (4;3;12). Найти ее координаты в цилиндрической системе координат.
Заданы координаты точки в сферической системе координат: 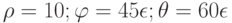 . Найти ее координаты в декартовой системе.
. Найти ее координаты в декартовой системе.
Найти длины отрезков отсекаемых на осях координат прямой проходящей через две точки, координаты которых: (3;7) и (8;3).
Задана матрица коэффициентов левой части системы линейных алгебраических уравнений:
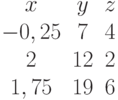
И одно из базисных решений:
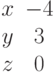
Найти методом Гаусса базисные решения.
Задана матрица коэффициентов левой части системы линейных алгебраических уравнений:
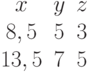
И одно из базисных решений:

Найти методом Гаусса базисные решения.
Область поиска решения задачи линейного программирования имеет вид выпуклого многоугольника с вершинами:
 | 20 | 0 | 0 | 10 |
 | 0 | 0 | 30 | 18 |
Целевая функция имеет вид.
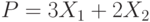
В какой вершине целевая функция достигает максимального значения.
Даны матрица левой части и столбец свободных членов системы линейных алгебраических уравнений.
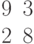
Найти второй вспомогательный определитель системы.
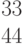
Даны матрица левой части и столбец свободных членов системы линейных алгебраических уравнений.
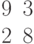
Найти решение методом Крамера.
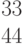
Дана матрица левой части и столбец свободных членов системы линейных алгебраических уравнений.
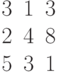
Вычислить первый вспомогательный определитель системы.
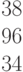
Дана матрица левой части и столбец свободных членов системы линейных алгебраических уравнений.
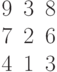
Вычислить третий вспомогательный определитель системы.

Заданы координаты точки (6;9). Найдите координаты после трансляции системы координат вдоль оси ОХ на a= 4 и вдоль оси ОУ на b=2.
После трансляции координаты точки приняли значение (8;7). Найдите координаты после трансляции системы координат вдоль оси ОХ на a= 5; вдоль оси ОУ на b= 4 и поворота против часовой стрелки на 30 градусов.
Заданы два уравнения кривых второго порядка:

Найти координаты точек их пересечения, если известны значения коэффициентов:
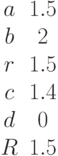
Заданы два уравнения кривых второго порядка:

Найти координаты точек их пересечения с точностью до второго знака после запятой.
Заданы два уравнения кривых второго порядка:

Найти координаты точек их пересечения, если известны значения коэффициентов:
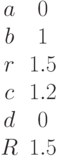
Заданы уравнения прямых в виде  и
и 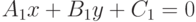 .
.

Найти угол между прямыми (в градусах).
Ответ введите с точностью до 1-го знака после запятой.Задано уравнение прямой в виде  .
.
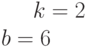
Найти угол в градусах между прямой и направлением оси ОХ.
Ответ введите с точностью до 1-го знака после запятой.Заданы уравнения двух прямых в виде  и
и  .
.

Угол (в градусах) между прямыми. Ответ введите с точностью до 1-го знака после запятой.
Найти отрезки, отсекаемые на осях координат (a на оси ОХ и b на оси OY) прямой проходящей через точку с координатами 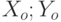 , если известно, что
, если известно, что 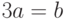 .
.
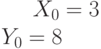
Найти отрезки, отсекаемые на осях координат (b на оси ОХ и b на оси OY) прямой проходящей через точку с координатами 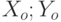 , если известно, что
, если известно, что 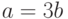 .
.
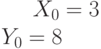
Заданы уравнения двух пересекающихся прямых:

Найти уравнения биссектрис углов образованных этими прямыми:

Известно, что:
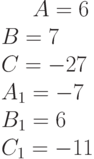
Задано параметрически уравнение эллипса:
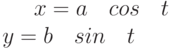
Значения  и
и 
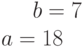
Какая из нижеприведенных точек лежит на этой кривой.
Даны полуоси гиперболы 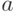 и
и  . Найти расстояние между ее фокусами.
. Найти расстояние между ее фокусами.
 Ответ введите с точностью до 2-го знака после запятой.
Ответ введите с точностью до 2-го знака после запятой.
Даны полуоси гиперболы  и
и  . Найти значение коэффициента
. Найти значение коэффициента  в ее уравнении в полярной системе координат. Ответ введите с точностью до 2-го знака после запятой.
в ее уравнении в полярной системе координат. Ответ введите с точностью до 2-го знака после запятой.
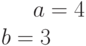
Задано уравнение кривой в виде: 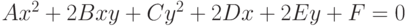 . Найти преобразование координат
. Найти преобразование координат 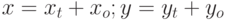 , при котором уравнение принимает вид:
, при котором уравнение принимает вид:
 . Указать значение
. Указать значение 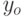 .
.

Задано уравнение кривой в виде: 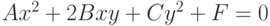 . Найти преобразование координат
. Найти преобразование координат  , которое приводит уравнение к виду:
, которое приводит уравнение к виду:
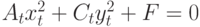 . Указать значение
. Указать значение  .
.
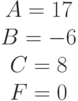
Задано уравнение кривой в виде: 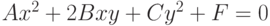 . Найти преобразование координат
. Найти преобразование координат 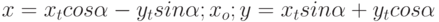 , которое приводит уравнение к виду:
, которое приводит уравнение к виду:
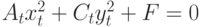 . Указать значение
. Указать значение 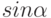 .
.
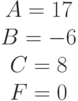
Задано уравнение кривой в виде: 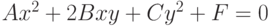 . Найти преобразование координат
. Найти преобразование координат 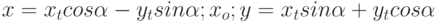 , которое приводит уравнение к виду:
, которое приводит уравнение к виду:
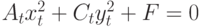 . Указать значение
. Указать значение 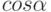 .
.

Найти расстояние от точки (1;2;4) до плоскости, если известны координаты точки и двух векторов лежащих в этой плоскости. Ответ введите с точностью до 2-го знака после запятой.
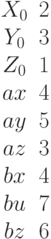
Найти угол между плоскостью заданной уравнением 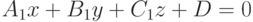 и плоскостью, если известны координаты точки и двух векторов лежащих в этой плоскости. Ответ введите с точностью до 1-го знака после запятой.
и плоскостью, если известны координаты точки и двух векторов лежащих в этой плоскости. Ответ введите с точностью до 1-го знака после запятой.
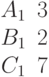
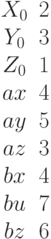
Найти расстояние от точки (1;2;4) до плоскости, если известны координаты трех точек лежащих в этой плоскости.

Задано уравнение плоскости в виде 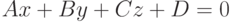 . Найти значения направляющих косинусов нормального вектора этой плоскости.
. Найти значения направляющих косинусов нормального вектора этой плоскости.
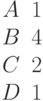
Задано уравнение плоскости в виде 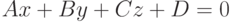 . Найти расстояние до плоскости от начала координат. Ответ введите с точностью до 3-го знака после запятой.
. Найти расстояние до плоскости от начала координат. Ответ введите с точностью до 3-го знака после запятой.
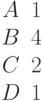
Найти угол (в градусах), под которым с координатной плоскостью YOZ пересекается прямая, образованная пересечением двух плоскостей, заданных уравнениями:
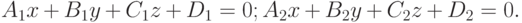

Найти угол (в градусах), под которым с координатной плоскостью ZOX пересекается прямая, образованная пересечением двух плоскостей, заданных уравнениями:
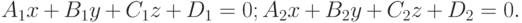

Найти координаты точки, в которой с координатной плоскостью XOY пересекается прямая, образованная пересечением двух плоскостей, заданных уравнениями:
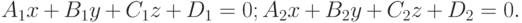
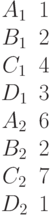
Составить уравнение плоскости проходящей через точку с координатами 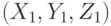 и прямую заданную уравнением:
и прямую заданную уравнением:
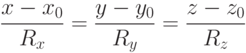
Уравнение представить в виде:
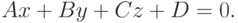
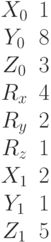
Составить уравнение плоскости проходящей через прямую, заданную уравнением:
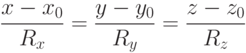
перпендикулярно плоскости:
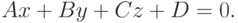
Уравнение представить в виде:
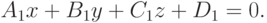
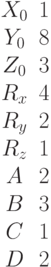
Укажите проекции направляющего вектора прямой, проходящей через точку 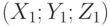 перпендикулярно к прямой заданной уравнением:
перпендикулярно к прямой заданной уравнением:
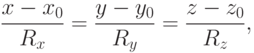

Найти кратчайшее расстояние от точки 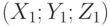 до прямой:
до прямой:
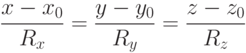

Дан однополостный гиперболоид. Его полуоси a, b, c. Выясните, какая из точек принадлежит однополосному гиперболоиду.
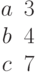
Дан двухполостный гиперболоид. Его полуоси a, b, c. Выясните, какая из точек принадлежит двухполосному гиперболоиду.
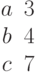
Определите, сколько общих точек имеет окружность радиуса R с центром в начале координат с прямой заданной уравнением 
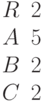
Определите, сколько общих точек имеет окружность радиуса R с центром в точке координатами (Xo;Yo) с прямой заданной уравнением  .
.
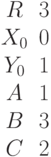
Дана расширенная матрица системы линейных алгебраических уравнений. Найти значения вспомогательных определителей.
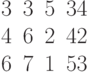
Заданы координаты точки в декартовой системе координат (7;4;2). Найти ее координаты в сферической системе.
Найти точки пересечения прямой, проходящей через точку с координатами (Xo,Yo,Zo) в направлении вектора (Rx,Ry,Rz), с поверхностью заданной уравнением:
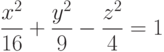
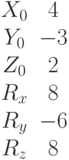
Заданы два уравнения кривых второго порядка:

Найти координаты точек их пересечения, если известны значения коэффициентов:
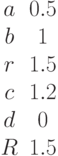
Задана матрица коэффициентов левой части системы линейных алгебраических уравнений:

И столбец свободных членов:
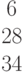
Найти методом Гаусса базисные решения.
Задано уравнение прямой в виде:  . Укажите, какое из уравнений вида:
. Укажите, какое из уравнений вида: 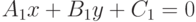 ; соответствует прямой перпендикулярной прямой заданной уравнением
; соответствует прямой перпендикулярной прямой заданной уравнением 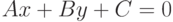 , и проходящей через точку
, и проходящей через точку 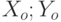 . Считать, что
. Считать, что
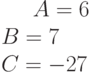
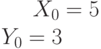
Задано уравнение прямой в виде  .
.
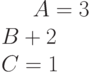
Найти расстояние от прямой до начала координат. Ответ введите с точностью до 2-го знака после запятой.
Дана матрица левой части и столбец свободных членов системы линейных алгебраических уравнений.
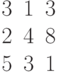
Вычислить главный определитель системы.
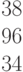
Найти коэффициенты уравнения прямой y=kx+b по координатам двух точек, через которые проходит прямая: (5;2) и (9;7).
Найти длины отрезков отсекаемых на осях координат прямой проходящей через две точки, координаты которых: (4;6) и (5;9).
Даны матрица левой части и столбец свободных членов системы линейных алгебраических уравнений.
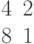
Найти решение методом Крамера.
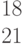
Дана матрица левой части и столбец свободных членов системы линейных алгебраических уравнений.
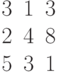
Вычислить третий вспомогательный определитель системы.
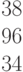
Заданы координаты точки (3;4). Найдите координаты после трансляции системы координат вдоль оси ОХ на a= 4 и поворота против часовой стрелки на 30 градусов.
Заданы два уравнения кривых второго порядка:

Найти координаты точек их пересечения, если известны значения коэффициентов:

Задано уравнение прямой в виде  .
.
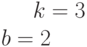
Найти угол в градусах между прямой и направлением оси ОХ.
Ответ введите с точностью до 1-го знака после запятой.Задано уравнение прямой в виде  .
.
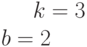
Расстояние между прямой и началом координат.
Ответ введите с точностью до 2-го знака после запятой.Найти отрезки, отсекаемые на осях координат (a на оси ОХ и b на оси OY) прямой проходящей через точку с координатами 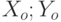 , если известно, что
, если известно, что 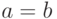 .
.
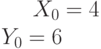
Найти отрезки, отсекаемые на осях координат (a на оси ОХ и b на оси OY) прямой проходящей через точку с координатами 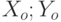 , если известно, что
, если известно, что 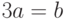 .
.
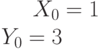
Найти отрезки, отсекаемые на осях координат (a на оси ОХ и b на оси OY) прямой проходящей через точку с координатами 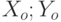 , если известно, что
, если известно, что 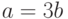 .
.
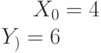
Задано параметрически уравнение эллипса:
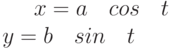
Значения  и
и 
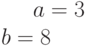
Какая из нижеприведенных точек лежит на этой кривой.
Даны полуоси эллипса.  и
и  . Найти расстояние между его фокусами.
. Найти расстояние между его фокусами.
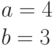 Ответ введите с точностью до 2-го знака после запятой.
Ответ введите с точностью до 2-го знака после запятой.
Даны полуоси гиперболы  и
и  . Найти ее эксцентриситет.
. Найти ее эксцентриситет.
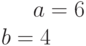 Ответ введите с точностью до 2-го знака после запятой.
Ответ введите с точностью до 2-го знака после запятой.
Найти уравнение плоскости в отрезках, если известны координаты точки и двух векторов лежащих в этой плоскости.
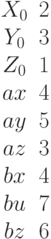
Задано уравнение плоскости в виде 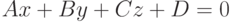 . Найти значения углов (в градусах) между нормальным вектором этой плоскости и координатными осями.
. Найти значения углов (в градусах) между нормальным вектором этой плоскости и координатными осями.
Задано уравнение плоскости в виде  . Найти значение недостающего косинуса. Ответ введите с точностью до 3-го знака после запятой.
. Найти значение недостающего косинуса. Ответ введите с точностью до 3-го знака после запятой.

Задано уравнение плоскости в виде 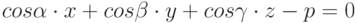 . Найти значение недостающего косинуса. Ответ введите с точностью до 3-го знака после запятой.
. Найти значение недостающего косинуса. Ответ введите с точностью до 3-го знака после запятой.
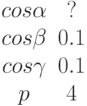
Найти координаты точки, в которой с координатной плоскостью YOZ пересекается прямая, образованная пересечением двух плоскостей, заданных уравнениями:
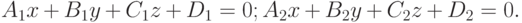
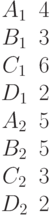
Найти угол (в градусах), под которым с координатной плоскостью ZOX пересекается прямая, образованная пересечением двух плоскостей, заданных уравнениями:
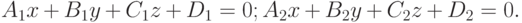
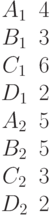
Найти координаты точки, в которой с координатной плоскостью XOY пересекается прямая, образованная пересечением двух плоскостей, заданных уравнениями:
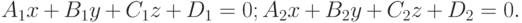

Найти кратчайшее расстояние от точки 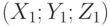 до прямой:
до прямой:
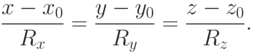

Определите, сколько общих точек имеет эллипс с посуосями a и b и центром в начале координат с прямой заданной уравнением  .
.
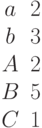
Дана расширенная матрица системы линейных алгебраических уравнений. Найти значения вспомогательных определителей.

Найти уравнение плоскости в виде 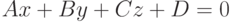 , если известны координаты точки и двух векторов лежащих в этой плоскости.
, если известны координаты точки и двух векторов лежащих в этой плоскости.
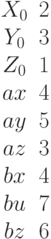
После трансляции координаты точки приняли значение (3;4). Найдите координаты до трансляции системы координат вдоль оси ОХ на a= 5; вдоль оси ОУ на b= 4 и повороте против часовой стрелки на 30 градусов.
Задано уравнение прямой в виде: 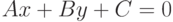 . Укажите, какое из уравнений вида:
. Укажите, какое из уравнений вида:  ; соответствует прямой перпендикулярной прямой заданной уравнением
; соответствует прямой перпендикулярной прямой заданной уравнением 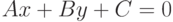 . Считать, что
. Считать, что

Найти точки пересечения прямой, проходящей через точку с координатами (Xo,Yo,Zo) в направлении вектора (Rx,Ry,Rz), с поверхностью заданной уравнением:
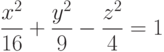
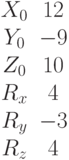
Дан однополостный гиперболоид. Его полуоси a, b, c. Выясните, какая из точек принадлежит однополосному гиперболоиду.
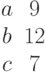
Заданы координаты точки в сферической системе координат:  . Найти ее координаты в декартовой системе.
. Найти ее координаты в декартовой системе.
Найти проекции на оси координат направляющего вектора прямой проходящей через две точки, координаты которых: (4;6) и (5;9).
Даны отрезки, отсекаемые прямой на осях координат: a=2; b=7. Найти координаты точки принадлежащей прямой: (5;…).
Задана матрица коэффициентов левой части системы линейных алгебраических уравнений:

И одно из базисных решений:

Найти методом Гаусса базисные решения.
Область поиска решения задачи линейного программирования имеет вид выпуклого многоугольника с вершинами:
 | 20 | 0 | 0 | 10 |
 | 0 | 0 | 30 | 18 |
Целевая функция имеет вид.
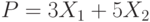
Даны матрица левой части и столбец свободных членов системы линейных алгебраических уравнений.

Найти первый вспомогательный определитель системы.
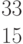
Заданы координаты точки (6;9). Найдите координаты после трансляции системы координат вдоль оси ОУ на b=7.
Заданы два уравнения кривых второго порядка:

Найти координаты точек их пересечения, если известны значения коэффициентов:
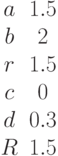
Заданы два уравнения кривых второго порядка:

Найти координаты точек их пересечения, если известны значения коэффициентов:
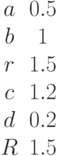
Заданы два уравнения кривых второго порядка:

Найти координаты точек их пересечения, если известны значения коэффициентов:

Заданы уравнения двух прямых в виде  и
и  .
.

Найти расстояние между прямыми.
Ответ введите с точностью до 2-го знака после запятой.Заданы уравнения двух пересекающихся прямых:

Найти уравнения биссектрис углов образованных этими прямыми:

Известно, что:
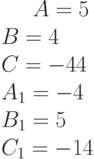
Задано уравнение кривой в виде: 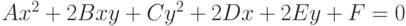 . Найти преобразование координат
. Найти преобразование координат 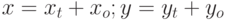 , при котором уравнение принимает вид:
, при котором уравнение принимает вид:
 . Указать значение
. Указать значение 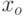 .
.

Задано уравнение плоскости в виде 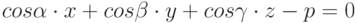 . Найти расстояние до этой плоскости от точки с координатами (1;2;3). Ответ введите с точностью до 2-го знака после запятой.
. Найти расстояние до этой плоскости от точки с координатами (1;2;3). Ответ введите с точностью до 2-го знака после запятой.

Найти проекции направляющего вектора прямой образованной пересечением двух плоскостей, заданных уравнениями:
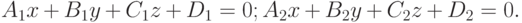

Найти угол, под которым с плоскостью
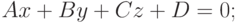
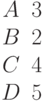
пересекается прямая, образованная пересечением двух плоскостей, заданных уравнениями:
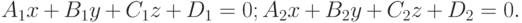

Найти точки пересечения прямой, проходящей через точку с координатами (Xo,Yo,Zo) в направлении вектора (Rx,Ry,Rz), с поверхностью заданной уравнением:
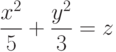

Найти точки пересечения прямой, проходящей через точку с координатами (Xo,Yo,Zo) в направлении вектора (Rx,Ry,Rz), с поверхностью эаданной уравнением:
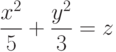
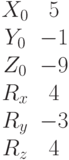
Заданы координаты точки в декартовой системе координат (3;2;5). Найти ее координаты в сферической системе.
Через точку с координатами (3;9) проходит прямая, направляющий вектор которой равен (5;4). Найти коэффициенты уравнения этой прямой: y=kx+b.
Задана матрица коэффициентов левой части системы линейных алгебраических уравнений:
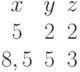
И одно из базисных решений:
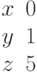
Найти методом Гаусса базисные решения.
Задано уравнение прямой в виде  .
.

Найти тупой угол в градусах между прямой и направлением оси ОХ.
Ответ введите с точностью до 1-го знака после запятой.Задано уравнение прямой в виде: 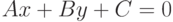 . Укажите, какое из уравнений вида:
. Укажите, какое из уравнений вида:  ; соответствует прямой параллельной прямой заданной уравнением
; соответствует прямой параллельной прямой заданной уравнением 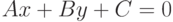 , и проходящей через точку
, и проходящей через точку 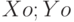 . Считать, что
. Считать, что
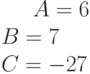
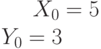
Найти уравнение плоскости в виде 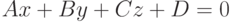 , если известны координаты точки и двух векторов лежащих в этой плоскости.
, если известны координаты точки и двух векторов лежащих в этой плоскости.
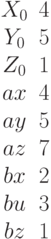
Задано уравнение плоскости в виде 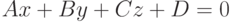 . Найти расстояние до плоскости от начала координат. Ответ введите с точностью до 3-го знака после запятой.
. Найти расстояние до плоскости от начала координат. Ответ введите с точностью до 3-го знака после запятой.
Задано уравнение плоскости в виде 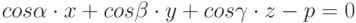 . Найти значение недостающего косинуса. Ответ введите с точностью до 3-го знака после запятой.
. Найти значение недостающего косинуса. Ответ введите с точностью до 3-го знака после запятой.

Составить уравнение плоскости проходящей через прямую уравнением:
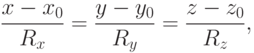
Параллельно прямой:

Уравнение представить в виде:
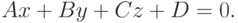

Дан двуполостный гиперболоид. Его полуоси a, b, c. Выясните, какая из точек принадлежит двухполосному гиперболоиду.
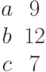
Определите, сколько общих точек имеет эллипс с посуосями a и b и центром в точке с координатами Xo, Yo с прямой заданной уравнением  .
.

Определите, сколько общих точек имеет окружность радиуса R с центром в точке координатами (Xo;Yo) с прямой заданной уравнением  .
.

Задано уравнение прямой в виде  .
.

Найти угол в градусах между прямой и направлением оси ОХ.
Ответ введите с точностью до 1-го знака после запятой.Найти координаты точки, в которой с координатной плоскостью ZOX пересекается прямая, образованная пересечением двух плоскостей, заданных уравнениями:
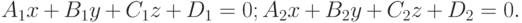
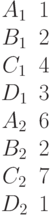
Даны матрица левой части и столбец свободных членов системы линейных алгебраических уравнений.

Найти второй вспомогательный определитель системы.
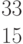
Даны полуоси эллипса  и
и  . Найти расстояние между его директрисами.
. Найти расстояние между его директрисами.
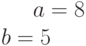 Ответ введите с точностью до 2-го знака после запятой.
Ответ введите с точностью до 2-го знака после запятой.
Задано уравнение кривой в виде: 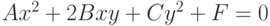 . Найти преобразование координат
. Найти преобразование координат  , которое приводит уравнение к виду:
, которое приводит уравнение к виду:
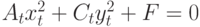 . Указать значение
. Указать значение  в градусах.
в градусах.

Найти угол между плоскостью заданной уравнением 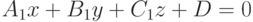 и плоскостью, если известны координаты трех точек лежащих в этой плоскости. Ответ введите в градусах с точностью до 1-го знака после запятой.
и плоскостью, если известны координаты трех точек лежащих в этой плоскости. Ответ введите в градусах с точностью до 1-го знака после запятой.

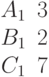
Определите, сколько общих точек имеет эллипс с посуосями a и b и центром в точке с координатами Xo, Yo с прямой заданной уравнением  .
.

Уравнение эллипса задано параметрически:
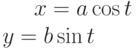
Значения  и
и 
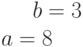
Какая из нижеприведенных точек лежит вне этой кривой?
Через точку с координатами (3;11) проходит прямая, направляющий вектор которой равен (1;4). Найти отрезки, отсекаемые этой прямой на осях координат.
Заданы координаты точки (6;9). Найдите координаты после трансляции системы координат вдоль оси ОХ на a= 5; вдоль оси ОУ на b= 4 и поворота против часовой стрелки на 30 градусов.
Заданы уравнения прямых в виде  и
и 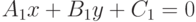 .
.

Найти угол между прямыми (в градусах).
Ответ введите с точностью до 1-го знака после запятой.Даны отрезки отсекаемые прямой на осях координат: a=4; b=4. Найти коэффициенты уравнения прямой : y=kx+b.
Найти квадрат площади треугольника, построенного на векторах:
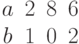
Ответ введите с точностью до 1-го знака после запятой.
Заданы два уравнения кривых второго порядка:

Найти координаты точек их пересечения, если известны значения коэффициентов:
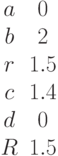

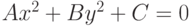 . Найти большую и малую полуоси.
. Найти большую и малую полуоси.
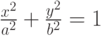



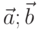
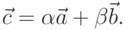







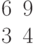
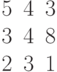
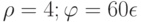 . Найти декартовы координаты этой точки.
. Найти декартовы координаты этой точки. 

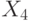
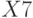

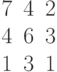

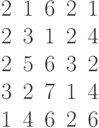
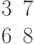
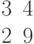
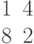
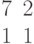
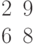






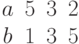

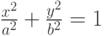
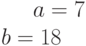
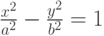
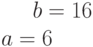
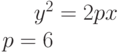
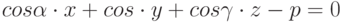
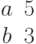
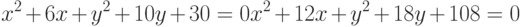
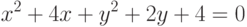

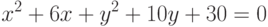
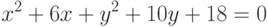
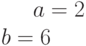
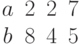 Ответ введите с точностью до 1-го знака после запятой.
Ответ введите с точностью до 1-го знака после запятой.


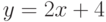 и
и 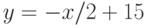 . Найдите угол (в градусах) между прямыми.
. Найдите угол (в градусах) между прямыми.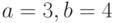 . Найдите значение
. Найдите значение  в точке с координатами:
в точке с координатами: 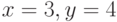 .
.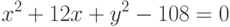

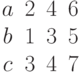

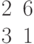
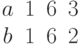
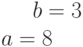
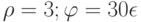 . Найти декартовы координаты этой точки.
. Найти декартовы координаты этой точки. 
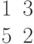
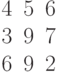
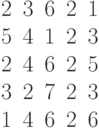
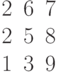

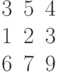
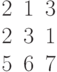

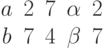

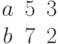

 . Найти значение угловых коэффициентов ее асимптот.
. Найти значение угловых коэффициентов ее асимптот.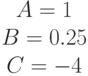

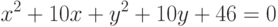



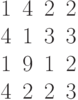
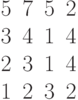




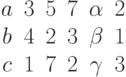
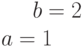
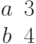
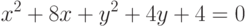
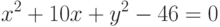
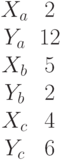
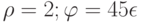 . Найти декартовы координаты этой точки.
. Найти декартовы координаты этой точки.