Разностные уравнения и задача Коши - ответы
Произведенные в год  товары
товары  представлены потребительскими товарами
представлены потребительскими товарами  и инвестиционными
и инвестиционными  . Инвестиции в год
. Инвестиции в год  зависят от прироста производства в прошлом году
зависят от прироста производства в прошлом году  по сравнению с позапрошлым
по сравнению с позапрошлым  . Потребление в год
. Потребление в год  зависит от выпуска продукции в прошлом году:
зависит от выпуска продукции в прошлом году:  . Таким образом:
. Таким образом:  . Если положить
. Если положить  , то разностное уравнение принимает вид:
, то разностное уравнение принимает вид:  . Вид решения этого уравнения зависит от значений корней характеристического уравнения:
. Вид решения этого уравнения зависит от значений корней характеристического уравнения:  .
.
Если это уравнение имеет единственное решение, то

Если характеристическое уравнение имеет два различных корня ( и
и  ), то
), то
 . (Считать, что
. (Считать, что  больше
больше  .) Если характеристическое уравнение имеет пару комплексно сопряженных корней:
.) Если характеристическое уравнение имеет пару комплексно сопряженных корней:  , где
, где  – мнимая единица, то:
– мнимая единица, то:
![Y_n=r^n[C_1\cos(n\varphi)+C_2\sin(n\varphi)]+b/(1-a)](https://intuit.ru//sites/default/files/tex_cache/4df86f122a56cf55f88562ae5133c189.png) . Коэффициенты
. Коэффициенты  и
и  могут быть определены из начальных условий для
могут быть определены из начальных условий для  и
и  .
.
 | 100 |
 | 110 |
 | 0,05 |
 | 0,3 |
 | 5 |
Найти значение  , входящего в выражение для корней характеристического уравнения. В ответе привести четыре знака после запятой.
, входящего в выражение для корней характеристического уравнения. В ответе привести четыре знака после запятой.
Общее решение некого дифференциального уравнения в частных производных имеет вид:  , где
, где  – произвольные постоянные.
– произвольные постоянные.
Задано что:
 |  |  |
|---|---|---|
| 2 | 3 | 422 |
| 3 | 4 | 1049 |
| 4 | 5 | 2110 |
| 2 | 2 | 238 |
| 3 | 5 | 1474 |
| 4 | 6 | 2780 |
| 5 | 7 | 4690 |
| 6 | 3 | 1918 |
Найти значения постоянных. В ответе указать значение 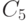 .
.
Произведенные в год  товары
товары  представлены потребительскими товарами
представлены потребительскими товарами  и инвестиционными
и инвестиционными  . Инвестиции в год
. Инвестиции в год  зависят от прироста производства в прошлом году
зависят от прироста производства в прошлом году  по сравнению с позапрошлым
по сравнению с позапрошлым  . Потребление в год
. Потребление в год  зависит от выпуска продукции в прошлом году:
зависит от выпуска продукции в прошлом году:  . Таким образом:
. Таким образом:  . Если положить
. Если положить  , то разностное уравнение принимает вид:
, то разностное уравнение принимает вид:  . Вид решения этого уравнения зависит от значений корней характеристического уравнения:
. Вид решения этого уравнения зависит от значений корней характеристического уравнения:  .
.
Если это уравнение имеет единственное решение, то

Если характеристическое уравнение имеет два различных корня ( и
и  ), то
), то
 . (Считать, что
. (Считать, что  больше
больше  .) Если характеристическое уравнение имеет пару комплексно сопряженных корней:
.) Если характеристическое уравнение имеет пару комплексно сопряженных корней:  , где
, где  – мнимая единица, то:
– мнимая единица, то:
![Y_n=r^n[C_1\cos(n\varphi)+C_2\sin(n\varphi)]+b/(1-a)](https://intuit.ru//sites/default/files/tex_cache/4df86f122a56cf55f88562ae5133c189.png) . Коэффициенты
. Коэффициенты  и
и  могут быть определены из начальных условий для
могут быть определены из начальных условий для  и
и  .
.
 | 100 |
 | 110 |
 | 0,04 |
 | 0,2 |
 | 3 |
Найти значение 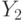 . В ответе привести один знак после запятой.
. В ответе привести один знак после запятой.
Общее решение некого дифференциального уравнения в частных производных имеет вид:  , где
, где  – произвольные постоянные.
– произвольные постоянные.
Задано что:
 |  |  |
|---|---|---|
| 2 | 3 | 422 |
| 3 | 4 | 1049 |
| 4 | 5 | 2110 |
| 2 | 2 | 238 |
| 3 | 5 | 1474 |
| 4 | 6 | 2780 |
| 5 | 7 | 4690 |
| 6 | 3 | 1918 |
Найти значения постоянных. В ответе указать значение 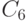 .
.
Произведенные в год  товары
товары  представлены потребительскими товарами
представлены потребительскими товарами  и инвестиционными
и инвестиционными  . Инвестиции в год
. Инвестиции в год  зависят от прироста производства в прошлом году
зависят от прироста производства в прошлом году  по сравнению с позапрошлым
по сравнению с позапрошлым  . Потребление в год
. Потребление в год  зависит от выпуска продукции в прошлом году:
зависит от выпуска продукции в прошлом году:  . Таким образом:
. Таким образом:  . Если положить
. Если положить  , то разностное уравнение принимает вид:
, то разностное уравнение принимает вид:  . Вид решения этого уравнения зависит от значений корней характеристического уравнения:
. Вид решения этого уравнения зависит от значений корней характеристического уравнения:  .
.
Если это уравнение имеет единственное решение, то

Если характеристическое уравнение имеет два различных корня ( и
и  ), то
), то
 . (Считать, что
. (Считать, что  больше
больше  .) Если характеристическое уравнение имеет пару комплексно сопряженных корней:
.) Если характеристическое уравнение имеет пару комплексно сопряженных корней:  , где
, где  – мнимая единица, то:
– мнимая единица, то:
![Y_n=r^n[C_1\cos(n\varphi)+C_2\sin(n\varphi)]+b/(1-a)](https://intuit.ru//sites/default/files/tex_cache/4df86f122a56cf55f88562ae5133c189.png) . Коэффициенты
. Коэффициенты  и
и  могут быть определены из начальных условий для
могут быть определены из начальных условий для  и
и  .
.
 | 100 |
 | 110 |
 | 0,05 |
 | 0,3 |
 | 5 |
Найти значение коэффициента  . В ответе привести один знак после запятой.
. В ответе привести один знак после запятой.
Общее решение некого дифференциального уравнения в частных производных имеет вид:  , где
, где  – произвольные постоянные.
– произвольные постоянные.
Задано что:
 |  |  |
|---|---|---|
| 2 | 3 | 166 |
| 3 | 4 | 408 |
| 4 | 5 | 814 |
| 2 | 2 | 100 |
| 3 | 5 | 566 |
| 4 | 6 | 1066 |
| 5 | 7 | 1794 |
| 6 | 3 | 782 |
Найти значения постоянных. В ответе указать значение  .
.
Общее решение некого дифференциального уравнения в частных производных имеет вид:  , где
, где  – произвольные постоянные.
– произвольные постоянные.
Задано что:
 |  |  |
|---|---|---|
| 2 | 3 | 422 |
| 3 | 4 | 1049 |
| 4 | 5 | 2110 |
| 2 | 2 | 238 |
| 3 | 5 | 1474 |
| 4 | 6 | 2780 |
| 5 | 7 | 4690 |
| 6 | 3 | 1918 |
Найти значения постоянных. В ответе указать значение 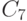 .
.
Общее решение некого дифференциального уравнения в частных производных имеет вид:  , где
, где  – произвольные постоянные.
– произвольные постоянные.
Задано что:
 |  |  |
|---|---|---|
| 2 | 3 | 422 |
| 3 | 4 | 1049 |
| 4 | 5 | 2110 |
| 2 | 2 | 238 |
| 3 | 5 | 1474 |
| 4 | 6 | 2780 |
| 5 | 7 | 4690 |
| 6 | 3 | 1918 |
Найти значения постоянных. В ответе указать значение  .
.
Произведенные в год  товары
товары  представлены потребительскими товарами
представлены потребительскими товарами  и инвестиционными
и инвестиционными  . Инвестиции в год
. Инвестиции в год  зависят от прироста производства в прошлом году
зависят от прироста производства в прошлом году  по сравнению с позапрошлым
по сравнению с позапрошлым  . Потребление в год
. Потребление в год  зависит от выпуска продукции в прошлом году:
зависит от выпуска продукции в прошлом году:  . Таким образом:
. Таким образом:  . Если положить
. Если положить  , то разностное уравнение принимает вид:
, то разностное уравнение принимает вид:  . Вид решения этого уравнения зависит от значений корней характеристического уравнения:
. Вид решения этого уравнения зависит от значений корней характеристического уравнения:  .
.
Если это уравнение имеет единственное решение, то

Если характеристическое уравнение имеет два различных корня ( и
и  ), то
), то
 . (Считать, что
. (Считать, что  больше
больше  .) Если характеристическое уравнение имеет пару комплексно сопряженных корней:
.) Если характеристическое уравнение имеет пару комплексно сопряженных корней:  , где
, где  – мнимая единица, то:
– мнимая единица, то:
![Y_n=r^n[C_1\cos(n\varphi)+C_2\sin(n\varphi)]+b/(1-a)](https://intuit.ru//sites/default/files/tex_cache/4df86f122a56cf55f88562ae5133c189.png) . Коэффициенты
. Коэффициенты  и
и  могут быть определены из начальных условий для
могут быть определены из начальных условий для  и
и  .
.
 | 100 |
 | 110 |
 | 0,03 |
 | 0,25 |
 | 7 |
Найти значение дискриминанта характеристического уравнения. В ответе привести четыре знака после запятой.
Произведенные в год  товары
товары  представлены потребительскими товарами
представлены потребительскими товарами  и инвестиционными
и инвестиционными  . Инвестиции в год
. Инвестиции в год  зависят от прироста производства в прошлом году
зависят от прироста производства в прошлом году  по сравнению с позапрошлым
по сравнению с позапрошлым  . Потребление в год
. Потребление в год  зависит от выпуска продукции в прошлом году:
зависит от выпуска продукции в прошлом году:  . Таким образом:
. Таким образом:  . Если положить
. Если положить  , то разностное уравнение принимает вид:
, то разностное уравнение принимает вид:  . Вид решения этого уравнения зависит от значений корней характеристического уравнения:
. Вид решения этого уравнения зависит от значений корней характеристического уравнения:  .
.
Если это уравнение имеет единственное решение, то

Если характеристическое уравнение имеет два различных корня ( и
и  ), то
), то
 . (Считать, что
. (Считать, что  больше
больше  .) Если характеристическое уравнение имеет пару комплексно сопряженных корней:
.) Если характеристическое уравнение имеет пару комплексно сопряженных корней:  , где
, где  – мнимая единица, то:
– мнимая единица, то:
![Y_n=r^n[C_1\cos(n\varphi)+C_2\sin(n\varphi)]+b/(1-a)](https://intuit.ru//sites/default/files/tex_cache/4df86f122a56cf55f88562ae5133c189.png) . Коэффициенты
. Коэффициенты  и
и  могут быть определены из начальных условий для
могут быть определены из начальных условий для  и
и  .
.
 | 100 |
 | 110 |
 | 0,04 |
 | 0,2 |
 | 3 |
Найти значение  , входящего в выражение для корней характеристического уравнения. В ответе привести четыре знака после запятой.
, входящего в выражение для корней характеристического уравнения. В ответе привести четыре знака после запятой.
Произведенные в год  товары
товары  представлены потребительскими товарами
представлены потребительскими товарами  и инвестиционными
и инвестиционными  . Инвестиции в год
. Инвестиции в год  зависят от прироста производства в прошлом году
зависят от прироста производства в прошлом году  по сравнению с позапрошлым
по сравнению с позапрошлым  . Потребление в год
. Потребление в год  зависит от выпуска продукции в прошлом году:
зависит от выпуска продукции в прошлом году:  . Таким образом:
. Таким образом:  . Если положить
. Если положить  , то разностное уравнение принимает вид:
, то разностное уравнение принимает вид:  . Вид решения этого уравнения зависит от значений корней характеристического уравнения:
. Вид решения этого уравнения зависит от значений корней характеристического уравнения:  .
.
Если это уравнение имеет единственное решение, то

Если характеристическое уравнение имеет два различных корня ( и
и  ), то
), то
 . (Считать, что
. (Считать, что  больше
больше  .) Если характеристическое уравнение имеет пару комплексно сопряженных корней:
.) Если характеристическое уравнение имеет пару комплексно сопряженных корней:  , где
, где  – мнимая единица, то:
– мнимая единица, то:
![Y_n=r^n[C_1\cos(n\varphi)+C_2\sin(n\varphi)]+b/(1-a)](https://intuit.ru//sites/default/files/tex_cache/4df86f122a56cf55f88562ae5133c189.png) . Коэффициенты
. Коэффициенты  и
и  могут быть определены из начальных условий для
могут быть определены из начальных условий для  и
и  .
.
 | 100 |
 | 110 |
 | 0,04 |
 | 0,2 |
 | 3 |
Найти значение коэффициента  . В ответе привести один знак после запятой.
. В ответе привести один знак после запятой.
Общее решение некого дифференциального уравнения в частных производных имеет вид:  , где
, где  – произвольные постоянные.
– произвольные постоянные.
Задано что:
 |  |  |
|---|---|---|
| 2 | 3 | 307 |
| 3 | 4 | 717 |
| 4 | 5 | 1391 |
| 2 | 2 | 174 |
| 3 | 5 | 1004 |
| 4 | 6 | 1828 |
| 5 | 7 | 3014 |
| 6 | 3 | 1223 |
Найти значения постоянных. В ответе указать значение 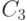 .
.
Произведенные в год  товары
товары  представлены потребительскими товарами
представлены потребительскими товарами  и инвестиционными
и инвестиционными  . Инвестиции в год
. Инвестиции в год  зависят от прироста производства в прошлом году
зависят от прироста производства в прошлом году  по сравнению с позапрошлым
по сравнению с позапрошлым  . Потребление в год
. Потребление в год  зависит от выпуска продукции в прошлом году:
зависит от выпуска продукции в прошлом году:  . Таким образом:
. Таким образом:  . Если положить
. Если положить  , то разностное уравнение принимает вид:
, то разностное уравнение принимает вид:  . Вид решения этого уравнения зависит от значений корней характеристического уравнения:
. Вид решения этого уравнения зависит от значений корней характеристического уравнения:  .
.
Если это уравнение имеет единственное решение, то

Если характеристическое уравнение имеет два различных корня ( и
и  ), то
), то
 . (Считать, что
. (Считать, что  больше
больше  .) Если характеристическое уравнение имеет пару комплексно сопряженных корней:
.) Если характеристическое уравнение имеет пару комплексно сопряженных корней:  , где
, где  – мнимая единица, то:
– мнимая единица, то:
![Y_n=r^n[C_1\cos(n\varphi)+C_2\sin(n\varphi)]+b/(1-a)](https://intuit.ru//sites/default/files/tex_cache/4df86f122a56cf55f88562ae5133c189.png) . Коэффициенты
. Коэффициенты  и
и  могут быть определены из начальных условий для
могут быть определены из начальных условий для  и
и  .
.
 | 100 |
 | 110 |
 | 0,05 |
 | 0,3 |
 | 5 |
Найти значение  (в радианах), входящего в выражение для корней характеристического уравнения. В ответе привести четыре знака после запятой.
(в радианах), входящего в выражение для корней характеристического уравнения. В ответе привести четыре знака после запятой.
Произведенные в год  товары
товары  представлены потребительскими товарами
представлены потребительскими товарами  и инвестиционными
и инвестиционными  . Инвестиции в год
. Инвестиции в год  зависят от прироста производства в прошлом году
зависят от прироста производства в прошлом году  по сравнению с позапрошлым
по сравнению с позапрошлым  . Потребление в год
. Потребление в год  зависит от выпуска продукции в прошлом году:
зависит от выпуска продукции в прошлом году:  . Таким образом:
. Таким образом:  . Если положить
. Если положить  , то разностное уравнение принимает вид:
, то разностное уравнение принимает вид:  . Вид решения этого уравнения зависит от значений корней характеристического уравнения:
. Вид решения этого уравнения зависит от значений корней характеристического уравнения:  .
.
Если это уравнение имеет единственное решение, то

Если характеристическое уравнение имеет два различных корня ( и
и  ), то
), то
 . (Считать, что
. (Считать, что  больше
больше  .) Если характеристическое уравнение имеет пару комплексно сопряженных корней:
.) Если характеристическое уравнение имеет пару комплексно сопряженных корней:  , где
, где  – мнимая единица, то:
– мнимая единица, то:
![Y_n=r^n[C_1\cos(n\varphi)+C_2\sin(n\varphi)]+b/(1-a)](https://intuit.ru//sites/default/files/tex_cache/4df86f122a56cf55f88562ae5133c189.png) . Коэффициенты
. Коэффициенты  и
и  могут быть определены из начальных условий для
могут быть определены из начальных условий для  и
и  .
.
 | 100 |
 | 110 |
 | 0,04 |
 | 0,2 |
 | 3 |
Найти значение модуля  корней характеристического уравнения. В ответе привести четыре знака после запятой.
корней характеристического уравнения. В ответе привести четыре знака после запятой.
Общее решение некого дифференциального уравнения в частных производных имеет вид:  , где
, где  – произвольные постоянные.
– произвольные постоянные.
Задано что:
 |  |  |
|---|---|---|
| 2 | 3 | 166 |
| 3 | 4 | 408 |
| 4 | 5 | 814 |
| 2 | 2 | 100 |
| 3 | 5 | 566 |
| 4 | 6 | 1066 |
| 5 | 7 | 1794 |
| 6 | 3 | 782 |
Найти значения постоянных. В ответе указать значение 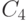 .
.
Общее решение некого дифференциального уравнения в частных производных имеет вид:  , где
, где  – произвольные постоянные.
– произвольные постоянные.
Задано что:
 |  |  |
|---|---|---|
| 2 | 3 | 307 |
| 3 | 4 | 717 |
| 4 | 5 | 1391 |
| 2 | 2 | 174 |
| 3 | 5 | 1004 |
| 4 | 6 | 1828 |
| 5 | 7 | 3014 |
| 6 | 3 | 1223 |
Найти значения постоянных. В ответе указать значение  .
.
Общее решение некого дифференциального уравнения в частных производных имеет вид:  , где
, где  – произвольные постоянные.
– произвольные постоянные.
Задано что:
 |  |  |
|---|---|---|
| 2 | 3 | 166 |
| 3 | 4 | 408 |
| 4 | 5 | 814 |
| 2 | 2 | 100 |
| 3 | 5 | 566 |
| 4 | 6 | 1066 |
| 5 | 7 | 1794 |
| 6 | 3 | 782 |
Найти значения постоянных. В ответе указать значение 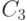 .
.
Общее решение некого дифференциального уравнения в частных производных имеет вид:  , где
, где  – произвольные постоянные.
– произвольные постоянные.
Задано что:
 |  |  |
|---|---|---|
| 2 | 3 | 422 |
| 3 | 4 | 1049 |
| 4 | 5 | 2110 |
| 2 | 2 | 238 |
| 3 | 5 | 1474 |
| 4 | 6 | 2780 |
| 5 | 7 | 4690 |
| 6 | 3 | 1918 |
Найти значения постоянных. В ответе указать значение 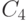 .
.
Общее решение некого дифференциального уравнения в частных производных имеет вид:  , где
, где  – произвольные постоянные.
– произвольные постоянные.
Задано что:
 |  |  |
|---|---|---|
| 2 | 3 | 166 |
| 3 | 4 | 408 |
| 4 | 5 | 814 |
| 2 | 2 | 100 |
| 3 | 5 | 566 |
| 4 | 6 | 1066 |
| 5 | 7 | 1794 |
| 6 | 3 | 782 |
Найти значения постоянных. В ответе указать значение 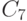 .
.
Общее решение некого дифференциального уравнения в частных производных имеет вид:  , где
, где  – произвольные постоянные.
– произвольные постоянные.
Задано что:
 |  |  |
|---|---|---|
| 2 | 3 | 166 |
| 3 | 4 | 408 |
| 4 | 5 | 814 |
| 2 | 2 | 100 |
| 3 | 5 | 566 |
| 4 | 6 | 1066 |
| 5 | 7 | 1794 |
| 6 | 3 | 782 |
Найти значения постоянных. В ответе указать значение  .
.
Произведенные в год  товары
товары  представлены потребительскими товарами
представлены потребительскими товарами  и инвестиционными
и инвестиционными  . Инвестиции в год
. Инвестиции в год  зависят от прироста производства в прошлом году
зависят от прироста производства в прошлом году  по сравнению с позапрошлым
по сравнению с позапрошлым  . Потребление в год
. Потребление в год  зависит от выпуска продукции в прошлом году:
зависит от выпуска продукции в прошлом году:  . Таким образом:
. Таким образом:  . Если положить
. Если положить  , то разностное уравнение принимает вид:
, то разностное уравнение принимает вид:  . Вид решения этого уравнения зависит от значений корней характеристического уравнения:
. Вид решения этого уравнения зависит от значений корней характеристического уравнения:  .
.
Если это уравнение имеет единственное решение, то

Если характеристическое уравнение имеет два различных корня ( и
и  ), то
), то
 . (Считать, что
. (Считать, что  больше
больше  .) Если характеристическое уравнение имеет пару комплексно сопряженных корней:
.) Если характеристическое уравнение имеет пару комплексно сопряженных корней:  , где
, где  – мнимая единица, то:
– мнимая единица, то:
![Y_n=r^n[C_1\cos(n\varphi)+C_2\sin(n\varphi)]+b/(1-a)](https://intuit.ru//sites/default/files/tex_cache/4df86f122a56cf55f88562ae5133c189.png) . Коэффициенты
. Коэффициенты  и
и  могут быть определены из начальных условий для
могут быть определены из начальных условий для  и
и  .
.
 | 100 |
 | 110 |
 | 0,05 |
 | 0,3 |
 | 5 |
Найти значение дискриминанта характеристического уравнения. В ответе привести четыре знака после запятой.
Произведенные в год  товары
товары  представлены потребительскими товарами
представлены потребительскими товарами  и инвестиционными
и инвестиционными  . Инвестиции в год
. Инвестиции в год  зависят от прироста производства в прошлом году
зависят от прироста производства в прошлом году  по сравнению с позапрошлым
по сравнению с позапрошлым  . Потребление в год
. Потребление в год  зависит от выпуска продукции в прошлом году:
зависит от выпуска продукции в прошлом году:  . Таким образом:
. Таким образом:  . Если положить
. Если положить  , то разностное уравнение принимает вид:
, то разностное уравнение принимает вид:  . Вид решения этого уравнения зависит от значений корней характеристического уравнения:
. Вид решения этого уравнения зависит от значений корней характеристического уравнения:  .
.
Если это уравнение имеет единственное решение, то

Если характеристическое уравнение имеет два различных корня ( и
и  ), то
), то
 . (Считать, что
. (Считать, что  больше
больше  .) Если характеристическое уравнение имеет пару комплексно сопряженных корней:
.) Если характеристическое уравнение имеет пару комплексно сопряженных корней:  , где
, где  – мнимая единица, то:
– мнимая единица, то:
![Y_n=r^n[C_1\cos(n\varphi)+C_2\sin(n\varphi)]+b/(1-a)](https://intuit.ru//sites/default/files/tex_cache/4df86f122a56cf55f88562ae5133c189.png) . Коэффициенты
. Коэффициенты  и
и  могут быть определены из начальных условий для
могут быть определены из начальных условий для  и
и  .
.
 | 100 |
 | 110 |
 | 0,05 |
 | 0,3 |
 | 5 |
Найти значение модуля  корней характеристического уравнения. В ответе привести четыре знака после запятой.
корней характеристического уравнения. В ответе привести четыре знака после запятой.
Произведенные в год  товары
товары  представлены потребительскими товарами
представлены потребительскими товарами  и инвестиционными
и инвестиционными  . Инвестиции в год
. Инвестиции в год  зависят от прироста производства в прошлом году
зависят от прироста производства в прошлом году  по сравнению с позапрошлым
по сравнению с позапрошлым  . Потребление в год
. Потребление в год  зависит от выпуска продукции в прошлом году:
зависит от выпуска продукции в прошлом году:  . Таким образом:
. Таким образом:  . Если положить
. Если положить  , то разностное уравнение принимает вид:
, то разностное уравнение принимает вид:  . Вид решения этого уравнения зависит от значений корней характеристического уравнения:
. Вид решения этого уравнения зависит от значений корней характеристического уравнения:  .
.
Если это уравнение имеет единственное решение, то

Если характеристическое уравнение имеет два различных корня ( и
и  ), то
), то
 . (Считать, что
. (Считать, что  больше
больше  .) Если характеристическое уравнение имеет пару комплексно сопряженных корней:
.) Если характеристическое уравнение имеет пару комплексно сопряженных корней:  , где
, где  – мнимая единица, то:
– мнимая единица, то:
![Y_n=r^n[C_1\cos(n\varphi)+C_2\sin(n\varphi)]+b/(1-a)](https://intuit.ru//sites/default/files/tex_cache/4df86f122a56cf55f88562ae5133c189.png) . Коэффициенты
. Коэффициенты  и
и  могут быть определены из начальных условий для
могут быть определены из начальных условий для  и
и  .
.
 | 100 |
 | 110 |
 | 0,03 |
 | 0,25 |
 | 7 |
Найти значение  , входящего в выражение для корней характеристического уравнения. В ответе привести четыре знака после запятой.
, входящего в выражение для корней характеристического уравнения. В ответе привести четыре знака после запятой.
Произведенные в год  товары
товары  представлены потребительскими товарами
представлены потребительскими товарами  и инвестиционными
и инвестиционными  . Инвестиции в год
. Инвестиции в год  зависят от прироста производства в прошлом году
зависят от прироста производства в прошлом году  по сравнению с позапрошлым
по сравнению с позапрошлым  . Потребление в год
. Потребление в год  зависит от выпуска продукции в прошлом году:
зависит от выпуска продукции в прошлом году:  . Таким образом:
. Таким образом:  . Если положить
. Если положить  , то разностное уравнение принимает вид:
, то разностное уравнение принимает вид:  . Вид решения этого уравнения зависит от значений корней характеристического уравнения:
. Вид решения этого уравнения зависит от значений корней характеристического уравнения:  .
.
Если это уравнение имеет единственное решение, то

Если характеристическое уравнение имеет два различных корня ( и
и  ), то
), то
 . (Считать, что
. (Считать, что  больше
больше  .) Если характеристическое уравнение имеет пару комплексно сопряженных корней:
.) Если характеристическое уравнение имеет пару комплексно сопряженных корней:  , где
, где  – мнимая единица, то:
– мнимая единица, то:
![Y_n=r^n[C_1\cos(n\varphi)+C_2\sin(n\varphi)]+b/(1-a)](https://intuit.ru//sites/default/files/tex_cache/4df86f122a56cf55f88562ae5133c189.png) . Коэффициенты
. Коэффициенты  и
и  могут быть определены из начальных условий для
могут быть определены из начальных условий для  и
и  .
.
 | 100 |
 | 110 |
 | 0,03 |
 | 0,25 |
 | 7 |
Найти значение  (в радианах), входящего в выражение для корней характеристического уравнения. В ответе привести четыре знака после запятой.
(в радианах), входящего в выражение для корней характеристического уравнения. В ответе привести четыре знака после запятой.
Произведенные в год  товары
товары  представлены потребительскими товарами
представлены потребительскими товарами  и инвестиционными
и инвестиционными  . Инвестиции в год
. Инвестиции в год  зависят от прироста производства в прошлом году
зависят от прироста производства в прошлом году  по сравнению с позапрошлым
по сравнению с позапрошлым  . Потребление в год
. Потребление в год  зависит от выпуска продукции в прошлом году:
зависит от выпуска продукции в прошлом году:  . Таким образом:
. Таким образом:  . Если положить
. Если положить  , то разностное уравнение принимает вид:
, то разностное уравнение принимает вид:  . Вид решения этого уравнения зависит от значений корней характеристического уравнения:
. Вид решения этого уравнения зависит от значений корней характеристического уравнения:  .
.
Если это уравнение имеет единственное решение, то

Если характеристическое уравнение имеет два различных корня ( и
и  ), то
), то
 . (Считать, что
. (Считать, что  больше
больше  .) Если характеристическое уравнение имеет пару комплексно сопряженных корней:
.) Если характеристическое уравнение имеет пару комплексно сопряженных корней:  , где
, где  – мнимая единица, то:
– мнимая единица, то:
![Y_n=r^n[C_1\cos(n\varphi)+C_2\sin(n\varphi)]+b/(1-a)](https://intuit.ru//sites/default/files/tex_cache/4df86f122a56cf55f88562ae5133c189.png) . Коэффициенты
. Коэффициенты  и
и  могут быть определены из начальных условий для
могут быть определены из начальных условий для  и
и  .
.
 | 100 |
 | 110 |
 | 0,05 |
 | 0,3 |
 | 5 |
Найти значение коэффициента  . В ответе привести один знак после запятой.
. В ответе привести один знак после запятой.
Произведенные в год  товары
товары  представлены потребительскими товарами
представлены потребительскими товарами  и инвестиционными
и инвестиционными  . Инвестиции в год
. Инвестиции в год  зависят от прироста производства в прошлом году
зависят от прироста производства в прошлом году  по сравнению с позапрошлым
по сравнению с позапрошлым  . Потребление в год
. Потребление в год  зависит от выпуска продукции в прошлом году:
зависит от выпуска продукции в прошлом году:  . Таким образом:
. Таким образом:  . Если положить
. Если положить  , то разностное уравнение принимает вид:
, то разностное уравнение принимает вид:  . Вид решения этого уравнения зависит от значений корней характеристического уравнения:
. Вид решения этого уравнения зависит от значений корней характеристического уравнения:  .
.
Если это уравнение имеет единственное решение, то

Если характеристическое уравнение имеет два различных корня ( и
и  ), то
), то
 . (Считать, что
. (Считать, что  больше
больше  .) Если характеристическое уравнение имеет пару комплексно сопряженных корней:
.) Если характеристическое уравнение имеет пару комплексно сопряженных корней:  , где
, где  – мнимая единица, то:
– мнимая единица, то:
![Y_n=r^n[C_1\cos(n\varphi)+C_2\sin(n\varphi)]+b/(1-a)](https://intuit.ru//sites/default/files/tex_cache/4df86f122a56cf55f88562ae5133c189.png) . Коэффициенты
. Коэффициенты  и
и  могут быть определены из начальных условий для
могут быть определены из начальных условий для  и
и  .
.
 | 100 |
 | 110 |
 | 0,04 |
 | 0,2 |
 | 3 |
Найти значение коэффициента  . В ответе привести один знак после запятой.
. В ответе привести один знак после запятой.
Произведенные в год  товары
товары  представлены потребительскими товарами
представлены потребительскими товарами  и инвестиционными
и инвестиционными  . Инвестиции в год
. Инвестиции в год  зависят от прироста производства в прошлом году
зависят от прироста производства в прошлом году  по сравнению с позапрошлым
по сравнению с позапрошлым  . Потребление в год
. Потребление в год  зависит от выпуска продукции в прошлом году:
зависит от выпуска продукции в прошлом году:  . Таким образом:
. Таким образом:  . Если положить
. Если положить  , то разностное уравнение принимает вид:
, то разностное уравнение принимает вид:  . Вид решения этого уравнения зависит от значений корней характеристического уравнения:
. Вид решения этого уравнения зависит от значений корней характеристического уравнения:  .
.
Если это уравнение имеет единственное решение, то

Если характеристическое уравнение имеет два различных корня ( и
и  ), то
), то
 . (Считать, что
. (Считать, что  больше
больше  .) Если характеристическое уравнение имеет пару комплексно сопряженных корней:
.) Если характеристическое уравнение имеет пару комплексно сопряженных корней:  , где
, где  – мнимая единица, то:
– мнимая единица, то:
![Y_n=r^n[C_1\cos(n\varphi)+C_2\sin(n\varphi)]+b/(1-a)](https://intuit.ru//sites/default/files/tex_cache/4df86f122a56cf55f88562ae5133c189.png) . Коэффициенты
. Коэффициенты  и
и  могут быть определены из начальных условий для
могут быть определены из начальных условий для  и
и  .
.
 | 100 |
 | 110 |
 | 0,03 |
 | 0,25 |
 | 7 |
Найти значение 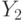 . В ответе привести один знак после запятой.
. В ответе привести один знак после запятой.
Общее решение некого дифференциального уравнения в частных производных имеет вид:  , где
, где  – произвольные постоянные.
– произвольные постоянные.
Задано что:
 |  |  |
|---|---|---|
| 2 | 3 | 307 |
| 3 | 4 | 717 |
| 4 | 5 | 1391 |
| 2 | 2 | 174 |
| 3 | 5 | 1004 |
| 4 | 6 | 1828 |
| 5 | 7 | 3014 |
| 6 | 3 | 1223 |
Найти значения постоянных. В ответе указать значение 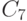 .
.
Общее решение некого дифференциального уравнения в частных производных имеет вид:  , где
, где  – произвольные постоянные.
– произвольные постоянные.
Задано что:
 |  |  |
|---|---|---|
| 2 | 3 | 166 |
| 3 | 4 | 408 |
| 4 | 5 | 814 |
| 2 | 2 | 100 |
| 3 | 5 | 566 |
| 4 | 6 | 1066 |
| 5 | 7 | 1794 |
| 6 | 3 | 782 |
Найти значения постоянных. В ответе указать значение 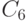 .
.
Произведенные в год  товары
товары  представлены потребительскими товарами
представлены потребительскими товарами  и инвестиционными
и инвестиционными  . Инвестиции в год
. Инвестиции в год  зависят от прироста производства в прошлом году
зависят от прироста производства в прошлом году  по сравнению с позапрошлым
по сравнению с позапрошлым  . Потребление в год
. Потребление в год  зависит от выпуска продукции в прошлом году:
зависит от выпуска продукции в прошлом году:  . Таким образом:
. Таким образом:  . Если положить
. Если положить  , то разностное уравнение принимает вид:
, то разностное уравнение принимает вид:  . Вид решения этого уравнения зависит от значений корней характеристического уравнения:
. Вид решения этого уравнения зависит от значений корней характеристического уравнения:  .
.
Если это уравнение имеет единственное решение, то

Если характеристическое уравнение имеет два различных корня ( и
и  ), то
), то
 . (Считать, что
. (Считать, что  больше
больше  .) Если характеристическое уравнение имеет пару комплексно сопряженных корней:
.) Если характеристическое уравнение имеет пару комплексно сопряженных корней:  , где
, где  – мнимая единица, то:
– мнимая единица, то:
![Y_n=r^n[C_1\cos(n\varphi)+C_2\sin(n\varphi)]+b/(1-a)](https://intuit.ru//sites/default/files/tex_cache/4df86f122a56cf55f88562ae5133c189.png) . Коэффициенты
. Коэффициенты  и
и  могут быть определены из начальных условий для
могут быть определены из начальных условий для  и
и  .
.
 | 100 |
 | 110 |
 | 0,05 |
 | 0,3 |
 | 5 |
Найти значение  , входящего в выражение для корней характеристического уравнения. В ответе привести четыре знака после запятой.
, входящего в выражение для корней характеристического уравнения. В ответе привести четыре знака после запятой.
Произведенные в год  товары
товары  представлены потребительскими товарами
представлены потребительскими товарами  и инвестиционными
и инвестиционными  . Инвестиции в год
. Инвестиции в год  зависят от прироста производства в прошлом году
зависят от прироста производства в прошлом году  по сравнению с позапрошлым
по сравнению с позапрошлым  . Потребление в год
. Потребление в год  зависит от выпуска продукции в прошлом году:
зависит от выпуска продукции в прошлом году:  . Таким образом:
. Таким образом:  . Если положить
. Если положить  , то разностное уравнение принимает вид:
, то разностное уравнение принимает вид:  . Вид решения этого уравнения зависит от значений корней характеристического уравнения:
. Вид решения этого уравнения зависит от значений корней характеристического уравнения:  .
.
Если это уравнение имеет единственное решение, то

Если характеристическое уравнение имеет два различных корня ( и
и  ), то
), то
 . (Считать, что
. (Считать, что  больше
больше  .) Если характеристическое уравнение имеет пару комплексно сопряженных корней:
.) Если характеристическое уравнение имеет пару комплексно сопряженных корней:  , где
, где  – мнимая единица, то:
– мнимая единица, то:
![Y_n=r^n[C_1\cos(n\varphi)+C_2\sin(n\varphi)]+b/(1-a)](https://intuit.ru//sites/default/files/tex_cache/4df86f122a56cf55f88562ae5133c189.png) . Коэффициенты
. Коэффициенты  и
и  могут быть определены из начальных условий для
могут быть определены из начальных условий для  и
и  .
.
 | 100 |
 | 110 |
 | 0,05 |
 | 0,3 |
 | 5 |
Найти значение 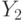 . В ответе привести один знак после запятой.
. В ответе привести один знак после запятой.
Произведенные в год  товары
товары  представлены потребительскими товарами
представлены потребительскими товарами  и инвестиционными
и инвестиционными  . Инвестиции в год
. Инвестиции в год  зависят от прироста производства в прошлом году
зависят от прироста производства в прошлом году  по сравнению с позапрошлым
по сравнению с позапрошлым  . Потребление в год
. Потребление в год  зависит от выпуска продукции в прошлом году:
зависит от выпуска продукции в прошлом году:  . Таким образом:
. Таким образом:  . Если положить
. Если положить  , то разностное уравнение принимает вид:
, то разностное уравнение принимает вид:  . Вид решения этого уравнения зависит от значений корней характеристического уравнения:
. Вид решения этого уравнения зависит от значений корней характеристического уравнения:  .
.
Если это уравнение имеет единственное решение, то

Если характеристическое уравнение имеет два различных корня ( и
и  ), то
), то
 . (Считать, что
. (Считать, что  больше
больше  .) Если характеристическое уравнение имеет пару комплексно сопряженных корней:
.) Если характеристическое уравнение имеет пару комплексно сопряженных корней:  , где
, где  – мнимая единица, то:
– мнимая единица, то:
![Y_n=r^n[C_1\cos(n\varphi)+C_2\sin(n\varphi)]+b/(1-a)](https://intuit.ru//sites/default/files/tex_cache/4df86f122a56cf55f88562ae5133c189.png) . Коэффициенты
. Коэффициенты  и
и  могут быть определены из начальных условий для
могут быть определены из начальных условий для  и
и  .
.
 | 100 |
 | 110 |
 | 0,04 |
 | 0,2 |
 | 3 |
Найти значение дискриминанта характеристического уравнения. В ответе привести четыре знака после запятой.
Общее решение некого дифференциального уравнения в частных производных имеет вид:  , где
, где  – произвольные постоянные.
– произвольные постоянные.
Задано что:
 |  |  |
|---|---|---|
| 2 | 3 | 307 |
| 3 | 4 | 717 |
| 4 | 5 | 1391 |
| 2 | 2 | 174 |
| 3 | 5 | 1004 |
| 4 | 6 | 1828 |
| 5 | 7 | 3014 |
| 6 | 3 | 1223 |
Найти значения постоянных. В ответе указать значение  .
.
Общее решение некого дифференциального уравнения в частных производных имеет вид:  , где
, где  – произвольные постоянные.
– произвольные постоянные.
Задано что:
 |  |  |
|---|---|---|
| 2 | 3 | 422 |
| 3 | 4 | 1049 |
| 4 | 5 | 2110 |
| 2 | 2 | 238 |
| 3 | 5 | 1474 |
| 4 | 6 | 2780 |
| 5 | 7 | 4690 |
| 6 | 3 | 1918 |
Найти значения постоянных. В ответе указать значение  .
.
Общее решение некого дифференциального уравнения в частных производных имеет вид:  , где
, где  – произвольные постоянные.
– произвольные постоянные.
Задано что:
 |  |  |
|---|---|---|
| 2 | 3 | 422 |
| 3 | 4 | 1049 |
| 4 | 5 | 2110 |
| 2 | 2 | 238 |
| 3 | 5 | 1474 |
| 4 | 6 | 2780 |
| 5 | 7 | 4690 |
| 6 | 3 | 1918 |
Найти значения постоянных. В ответе указать значение 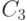 .
.
Общее решение некого дифференциального уравнения в частных производных имеет вид:  , где
, где  – произвольные постоянные.
– произвольные постоянные.
Задано что:
 |  |  |
|---|---|---|
| 2 | 3 | 307 |
| 3 | 4 | 717 |
| 4 | 5 | 1391 |
| 2 | 2 | 174 |
| 3 | 5 | 1004 |
| 4 | 6 | 1828 |
| 5 | 7 | 3014 |
| 6 | 3 | 1223 |
Найти значения постоянных. В ответе указать значение 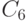 .
.
Общее решение некого дифференциального уравнения в частных производных имеет вид:  , где
, где  – произвольные постоянные.
– произвольные постоянные.
Задано что:
 |  |  |
|---|---|---|
| 2 | 3 | 307 |
| 3 | 4 | 717 |
| 4 | 5 | 1391 |
| 2 | 2 | 174 |
| 3 | 5 | 1004 |
| 4 | 6 | 1828 |
| 5 | 7 | 3014 |
| 6 | 3 | 1223 |
Найти значения постоянных. В ответе указать значение  .
.
Общее решение некого дифференциального уравнения в частных производных имеет вид:  , где
, где  – произвольные постоянные.
– произвольные постоянные.
Задано что:
 |  |  |
|---|---|---|
| 2 | 3 | 166 |
| 3 | 4 | 408 |
| 4 | 5 | 814 |
| 2 | 2 | 100 |
| 3 | 5 | 566 |
| 4 | 6 | 1066 |
| 5 | 7 | 1794 |
| 6 | 3 | 782 |
Найти значения постоянных. В ответе указать значение 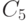 .
.
Произведенные в год  товары
товары  представлены потребительскими товарами
представлены потребительскими товарами  и инвестиционными
и инвестиционными  . Инвестиции в год
. Инвестиции в год  зависят от прироста производства в прошлом году
зависят от прироста производства в прошлом году  по сравнению с позапрошлым
по сравнению с позапрошлым  . Потребление в год
. Потребление в год  зависит от выпуска продукции в прошлом году:
зависит от выпуска продукции в прошлом году:  . Таким образом:
. Таким образом:  . Если положить
. Если положить  , то разностное уравнение принимает вид:
, то разностное уравнение принимает вид:  . Вид решения этого уравнения зависит от значений корней характеристического уравнения:
. Вид решения этого уравнения зависит от значений корней характеристического уравнения:  .
.
Если это уравнение имеет единственное решение, то

Если характеристическое уравнение имеет два различных корня ( и
и  ), то
), то
 . (Считать, что
. (Считать, что  больше
больше  .) Если характеристическое уравнение имеет пару комплексно сопряженных корней:
.) Если характеристическое уравнение имеет пару комплексно сопряженных корней:  , где
, где  – мнимая единица, то:
– мнимая единица, то:
![Y_n=r^n[C_1\cos(n\varphi)+C_2\sin(n\varphi)]+b/(1-a)](https://intuit.ru//sites/default/files/tex_cache/4df86f122a56cf55f88562ae5133c189.png) . Коэффициенты
. Коэффициенты  и
и  могут быть определены из начальных условий для
могут быть определены из начальных условий для  и
и  .
.
 | 100 |
 | 110 |
 | 0,03 |
 | 0,25 |
 | 7 |
Найти значение модуля  корней характеристического уравнения. В ответе привести четыре знака после запятой.
корней характеристического уравнения. В ответе привести четыре знака после запятой.
Общее решение некого дифференциального уравнения в частных производных имеет вид:  , где
, где  – произвольные постоянные.
– произвольные постоянные.
Задано что:
 |  |  |
|---|---|---|
| 2 | 3 | 422 |
| 3 | 4 | 1049 |
| 4 | 5 | 2110 |
| 2 | 2 | 238 |
| 3 | 5 | 1474 |
| 4 | 6 | 2780 |
| 5 | 7 | 4690 |
| 6 | 3 | 1918 |
Найти значения постоянных. В ответе указать значение  .
.
Общее решение некого дифференциального уравнения в частных производных имеет вид:  , где
, где  – произвольные постоянные.
– произвольные постоянные.
Задано что:
 |  |  |
|---|---|---|
| 2 | 3 | 307 |
| 3 | 4 | 717 |
| 4 | 5 | 1391 |
| 2 | 2 | 174 |
| 3 | 5 | 1004 |
| 4 | 6 | 1828 |
| 5 | 7 | 3014 |
| 6 | 3 | 1223 |
Найти значения постоянных. В ответе указать значение 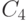 .
.
Произведенные в год  товары
товары  представлены потребительскими товарами
представлены потребительскими товарами  и инвестиционными
и инвестиционными  . Инвестиции в год
. Инвестиции в год  зависят от прироста производства в прошлом году
зависят от прироста производства в прошлом году  по сравнению с позапрошлым
по сравнению с позапрошлым  . Потребление в год
. Потребление в год  зависит от выпуска продукции в прошлом году:
зависит от выпуска продукции в прошлом году:  . Таким образом:
. Таким образом:  . Если положить
. Если положить  , то разностное уравнение принимает вид:
, то разностное уравнение принимает вид:  . Вид решения этого уравнения зависит от значений корней характеристического уравнения:
. Вид решения этого уравнения зависит от значений корней характеристического уравнения:  .
.
Если это уравнение имеет единственное решение, то

Если характеристическое уравнение имеет два различных корня ( и
и  ), то
), то
 . (Считать, что
. (Считать, что  больше
больше  .) Если характеристическое уравнение имеет пару комплексно сопряженных корней:
.) Если характеристическое уравнение имеет пару комплексно сопряженных корней:  , где
, где  – мнимая единица, то:
– мнимая единица, то:
![Y_n=r^n[C_1\cos(n\varphi)+C_2\sin(n\varphi)]+b/(1-a)](https://intuit.ru//sites/default/files/tex_cache/4df86f122a56cf55f88562ae5133c189.png) . Коэффициенты
. Коэффициенты  и
и  могут быть определены из начальных условий для
могут быть определены из начальных условий для  и
и  .
.
 | 100 |
 | 110 |
 | 0,04 |
 | 0,2 |
 | 3 |
Найти значение  (в радианах), входящего в выражение для корней характеристического уравнения. В ответе привести четыре знака после запятой.
(в радианах), входящего в выражение для корней характеристического уравнения. В ответе привести четыре знака после запятой.
Произведенные в год  товары
товары  представлены потребительскими товарами
представлены потребительскими товарами  и инвестиционными
и инвестиционными  . Инвестиции в год
. Инвестиции в год  зависят от прироста производства в прошлом году
зависят от прироста производства в прошлом году  по сравнению с позапрошлым
по сравнению с позапрошлым  . Потребление в год
. Потребление в год  зависит от выпуска продукции в прошлом году:
зависит от выпуска продукции в прошлом году:  . Таким образом:
. Таким образом:  . Если положить
. Если положить  , то разностное уравнение принимает вид:
, то разностное уравнение принимает вид:  . Вид решения этого уравнения зависит от значений корней характеристического уравнения:
. Вид решения этого уравнения зависит от значений корней характеристического уравнения:  .
.
Если это уравнение имеет единственное решение, то

Если характеристическое уравнение имеет два различных корня ( и
и  ), то
), то
 . (Считать, что
. (Считать, что  больше
больше  .) Если характеристическое уравнение имеет пару комплексно сопряженных корней:
.) Если характеристическое уравнение имеет пару комплексно сопряженных корней:  , где
, где  – мнимая единица, то:
– мнимая единица, то:
![Y_n=r^n[C_1\cos(n\varphi)+C_2\sin(n\varphi)]+b/(1-a)](https://intuit.ru//sites/default/files/tex_cache/4df86f122a56cf55f88562ae5133c189.png) . Коэффициенты
. Коэффициенты  и
и  могут быть определены из начальных условий для
могут быть определены из начальных условий для  и
и  .
.
 | 100 |
 | 110 |
 | 0,03 |
 | 0,25 |
 | 7 |
Найти значение коэффициента  . В ответе привести один знак после запятой.
. В ответе привести один знак после запятой.
Общее решение некого дифференциального уравнения в частных производных имеет вид:  , где
, где  – произвольные постоянные.
– произвольные постоянные.
Задано что:
 |  |  |
|---|---|---|
| 2 | 3 | 307 |
| 3 | 4 | 717 |
| 4 | 5 | 1391 |
| 2 | 2 | 174 |
| 3 | 5 | 1004 |
| 4 | 6 | 1828 |
| 5 | 7 | 3014 |
| 6 | 3 | 1223 |
Найти значения постоянных. В ответе указать значение 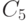 .
.
Произведенные в год  товары
товары  представлены потребительскими товарами
представлены потребительскими товарами  и инвестиционными
и инвестиционными  . Инвестиции в год
. Инвестиции в год  зависят от прироста производства в прошлом году
зависят от прироста производства в прошлом году  по сравнению с позапрошлым
по сравнению с позапрошлым  . Потребление в год
. Потребление в год  зависит от выпуска продукции в прошлом году:
зависит от выпуска продукции в прошлом году:  . Таким образом:
. Таким образом:  . Если положить
. Если положить  , то разностное уравнение принимает вид:
, то разностное уравнение принимает вид:  . Вид решения этого уравнения зависит от значений корней характеристического уравнения:
. Вид решения этого уравнения зависит от значений корней характеристического уравнения:  .
.
Если это уравнение имеет единственное решение, то

Если характеристическое уравнение имеет два различных корня ( и
и  ), то
), то
 . (Считать, что
. (Считать, что  больше
больше  .) Если характеристическое уравнение имеет пару комплексно сопряженных корней:
.) Если характеристическое уравнение имеет пару комплексно сопряженных корней:  , где
, где  – мнимая единица, то:
– мнимая единица, то:
![Y_n=r^n[C_1\cos(n\varphi)+C_2\sin(n\varphi)]+b/(1-a)](https://intuit.ru//sites/default/files/tex_cache/4df86f122a56cf55f88562ae5133c189.png) . Коэффициенты
. Коэффициенты  и
и  могут быть определены из начальных условий для
могут быть определены из начальных условий для  и
и  .
.
 | 100 |
 | 110 |
 | 0,03 |
 | 0,25 |
 | 7 |
Найти значение  , входящего в выражение для корней характеристического уравнения. В ответе привести четыре знака после запятой.
, входящего в выражение для корней характеристического уравнения. В ответе привести четыре знака после запятой.
Произведенные в год  товары
товары  представлены потребительскими товарами
представлены потребительскими товарами  и инвестиционными
и инвестиционными  . Инвестиции в год
. Инвестиции в год  зависят от прироста производства в прошлом году
зависят от прироста производства в прошлом году  по сравнению с позапрошлым
по сравнению с позапрошлым  . Потребление в год
. Потребление в год  зависит от выпуска продукции в прошлом году:
зависит от выпуска продукции в прошлом году:  . Таким образом:
. Таким образом:  . Если положить
. Если положить  , то разностное уравнение принимает вид:
, то разностное уравнение принимает вид:  . Вид решения этого уравнения зависит от значений корней характеристического уравнения:
. Вид решения этого уравнения зависит от значений корней характеристического уравнения:  .
.
Если это уравнение имеет единственное решение, то

Если характеристическое уравнение имеет два различных корня ( и
и  ), то
), то
 . (Считать, что
. (Считать, что  больше
больше  .) Если характеристическое уравнение имеет пару комплексно сопряженных корней:
.) Если характеристическое уравнение имеет пару комплексно сопряженных корней:  , где
, где  – мнимая единица, то:
– мнимая единица, то:
![Y_n=r^n[C_1\cos(n\varphi)+C_2\sin(n\varphi)]+b/(1-a)](https://intuit.ru//sites/default/files/tex_cache/4df86f122a56cf55f88562ae5133c189.png) . Коэффициенты
. Коэффициенты  и
и  могут быть определены из начальных условий для
могут быть определены из начальных условий для  и
и  .
.
 | 100 |
 | 110 |
 | 0,04 |
 | 0,2 |
 | 3 |
Найти значение  , входящего в выражение для корней характеристического уравнения. В ответе привести четыре знака после запятой.
, входящего в выражение для корней характеристического уравнения. В ответе привести четыре знака после запятой.
Произведенные в год  товары
товары  представлены потребительскими товарами
представлены потребительскими товарами  и инвестиционными
и инвестиционными  . Инвестиции в год
. Инвестиции в год  зависят от прироста производства в прошлом году
зависят от прироста производства в прошлом году  по сравнению с позапрошлым
по сравнению с позапрошлым  . Потребление в год
. Потребление в год  зависит от выпуска продукции в прошлом году:
зависит от выпуска продукции в прошлом году:  . Таким образом:
. Таким образом:  . Если положить
. Если положить  , то разностное уравнение принимает вид:
, то разностное уравнение принимает вид:  . Вид решения этого уравнения зависит от значений корней характеристического уравнения:
. Вид решения этого уравнения зависит от значений корней характеристического уравнения:  .
.
Если это уравнение имеет единственное решение, то

Если характеристическое уравнение имеет два различных корня ( и
и  ), то
), то
 . (Считать, что
. (Считать, что  больше
больше  .) Если характеристическое уравнение имеет пару комплексно сопряженных корней:
.) Если характеристическое уравнение имеет пару комплексно сопряженных корней:  , где
, где  – мнимая единица, то:
– мнимая единица, то:
![Y_n=r^n[C_1\cos(n\varphi)+C_2\sin(n\varphi)]+b/(1-a)](https://intuit.ru//sites/default/files/tex_cache/4df86f122a56cf55f88562ae5133c189.png) . Коэффициенты
. Коэффициенты  и
и  могут быть определены из начальных условий для
могут быть определены из начальных условий для  и
и  .
.
 | 100 |
 | 110 |
 | 0,03 |
 | 0,25 |
 | 7 |
Найти значение коэффициента  . В ответе привести один знак после запятой.
. В ответе привести один знак после запятой.
