Коэффициент множественной корреляции 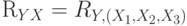 между выходной (результирующей) переменной
между выходной (результирующей) переменной  и входными (объясняющими) переменными
и входными (объясняющими) переменными 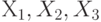 обладает следующими свойствами
обладает следующими свойствами
(Ответ считается верным, если отмечены все правильные варианты ответов.)
Варианты ответа
 (Верный ответ)
(Верный ответ)
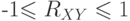
если 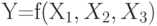 , то
, то 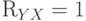 (Верный ответ)
(Верный ответ)
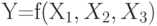 , то
, то 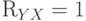 (Верный ответ)
(Верный ответ)
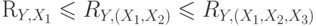 (Верный ответ)
(Верный ответ)
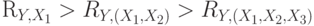

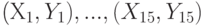 вычислен выборочный коэффициент корреляции
вычислен выборочный коэффициент корреляции 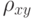 . Какое распределение имеет статистика
. Какое распределение имеет статистика  в том случае, когда случайные величины
в том случае, когда случайные величины  и
и 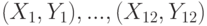 вычислен выборочный коэффициент корреляции
вычислен выборочный коэффициент корреляции 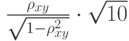 в том случае, когда случайные величины
в том случае, когда случайные величины 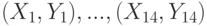 вычислен выборочный коэффициент корреляции
вычислен выборочный коэффициент корреляции 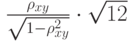 в том случае, когда случайные величины
в том случае, когда случайные величины 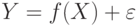 , в которой
, в которой  - ненаблюдаемая случайная помеха с нулевым математическим ожиданием. Предполагается, что случайные величины X и
- ненаблюдаемая случайная помеха с нулевым математическим ожиданием. Предполагается, что случайные величины X и 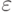 независимы. Корреляционным отношением переменной
независимы. Корреляционным отношением переменной 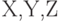 :
: 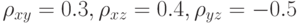 Частный коэффициент корреляции случайных величин
Частный коэффициент корреляции случайных величин  будет
будет Частный коэффициент корреляции случайных величин
Частный коэффициент корреляции случайных величин 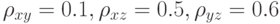 Частный коэффициент корреляции случайных величин
Частный коэффициент корреляции случайных величин 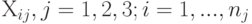 описываются моделью следующего вида
описываются моделью следующего вида  , где
, где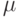 -неизвестное общее среднее,
-неизвестное общее среднее, 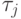 -отклонение от среднего, вызванное изменением уровня факторной переменной,
-отклонение от среднего, вызванное изменением уровня факторной переменной, 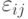 - погрешности с нулевым математическим ожиданием.Контраст
- погрешности с нулевым математическим ожиданием.Контраст 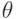 параметров
параметров 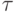 в этой модели задан следующим образом
в этой модели задан следующим образом 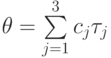 , где
, где 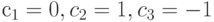 .Определенный таким образом контраст характеризует
.Определенный таким образом контраст характеризует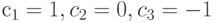 .Определенный таким образом контраст характеризует
.Определенный таким образом контраст характеризует .Определенный таким образом контраст характеризует
.Определенный таким образом контраст характеризует