Статистические методы анализа данных - ответы
Количество вопросов - 72

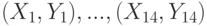 вычислен выборочный коэффициент корреляции
вычислен выборочный коэффициент корреляции 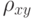 . Какое распределение имеет статистика
. Какое распределение имеет статистика 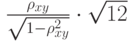 в том случае, когда случайные величины
в том случае, когда случайные величины  и
и  независимы?
независимы? и
и  измерены в номинальной шкале. Какой критерий можно применить для проверки гипотезы о независимости этих признаков?
измерены в номинальной шкале. Какой критерий можно применить для проверки гипотезы о независимости этих признаков?  и
и  , измеренных в номинальной шкале, составлена таблица сопряженности 2х2 и вычислен коэффициент ассоциации Юла. Этот коэффициент
, измеренных в номинальной шкале, составлена таблица сопряженности 2х2 и вычислен коэффициент ассоциации Юла. Этот коэффициент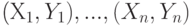 известного объема n вычислен выборочный коэффициент корреляции
известного объема n вычислен выборочный коэффициент корреляции 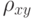 . Имея эту информацию, можно
. Имея эту информацию, можно и
и  , измеренных в номинальной шкале, составлена таблица сопряженности и вычислена мера Гутмана
, измеренных в номинальной шкале, составлена таблица сопряженности и вычислена мера Гутмана  . Полученное значение следует трактовать таким образом:
. Полученное значение следует трактовать таким образом:  и
и  оказался равным 0.6. Эта информация
оказался равным 0.6. Эта информация  - МНК-оценка неизвестного регрессионного параметра
- МНК-оценка неизвестного регрессионного параметра 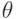 ,
,  - любая несмещенная оценка этого параметра, а
- любая несмещенная оценка этого параметра, а  - некоторый детерминированный вектор. Неравенство
- некоторый детерминированный вектор. Неравенство 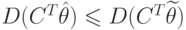 выполняется
выполняется 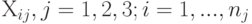 описываются моделью следующего вида
описываются моделью следующего вида  , где
, где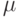 -неизвестное общее среднее,
-неизвестное общее среднее, 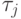 -отклонение от среднего, вызванное изменением уровня факторной переменной,
-отклонение от среднего, вызванное изменением уровня факторной переменной, 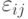 - погрешности с нулевым математическим ожиданием.Контраст
- погрешности с нулевым математическим ожиданием.Контраст 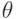 параметров
параметров 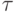 в этой модели задан следующим образом
в этой модели задан следующим образом 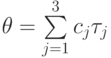 , где
, где  .Определенный таким образом контраст характеризует
.Определенный таким образом контраст характеризует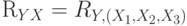 между выходной (результирующей) переменной
между выходной (результирующей) переменной  и входными (объясняющими) переменными
и входными (объясняющими) переменными 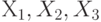 обладает следующими свойствами
обладает следующими свойствами , имеющего 6 градаций, и номинального признака
, имеющего 6 градаций, и номинального признака  , имеющего 3 градации, составлена таблица сопряженности и вычислено значение статистики хи-квадрат. Значение статистики оказалось равным 20.67. Согласно таблицам, квантили распределения хи-квадрат
, имеющего 3 градации, составлена таблица сопряженности и вычислено значение статистики хи-квадрат. Значение статистики оказалось равным 20.67. Согласно таблицам, квантили распределения хи-квадрат 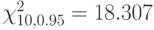 ,
, 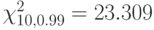 .Какой (какие) выводы можно сделать, опираясь на полученный результат?
.Какой (какие) выводы можно сделать, опираясь на полученный результат?  и
и  , измеренных в номинальной шкале, составлена таблица сопряженности и вычислен коэффициент среднеквадратической сопряженности
, измеренных в номинальной шкале, составлена таблица сопряженности и вычислен коэффициент среднеквадратической сопряженности  . Полученный результат можно трактовать следующим образом
. Полученный результат можно трактовать следующим образом :
: 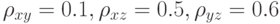 Частный коэффициент корреляции случайных величин
Частный коэффициент корреляции случайных величин  и
и  при фиксированном значении
при фиксированном значении  будет
будет измеряется в номинальной шкале и имеет 3 градаций, переменная
измеряется в номинальной шкале и имеет 3 градаций, переменная  измеряется в номинальной шкале и имеет 2 градации. Для того чтобы выяснить, являются ли переменные
измеряется в номинальной шкале и имеет 2 градации. Для того чтобы выяснить, являются ли переменные  и
и  зависимыми, применяют критерий хи-квадрат. Какое число степеней свободы будет иметь статистика хи-квадрат в случае справедливости основной гипотезы?
зависимыми, применяют критерий хи-квадрат. Какое число степеней свободы будет иметь статистика хи-квадрат в случае справедливости основной гипотезы? 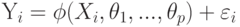 ,
, 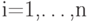 , где
, где 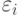 - ненаблюдаемые центрированные погрешности, имеющие плотность распределения
- ненаблюдаемые центрированные погрешности, имеющие плотность распределения 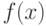 . Для оценивания неизвестных параметров
. Для оценивания неизвестных параметров 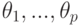 применен ранговый метод. Величины дисперсий
применен ранговый метод. Величины дисперсий 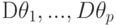 , полученных R-оценок, зависят от
, полученных R-оценок, зависят от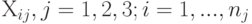 описываются моделью следующего вида
описываются моделью следующего вида  , где
, где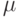 -неизвестное общее среднее,
-неизвестное общее среднее, 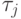 -отклонение от среднего, вызванное изменением уровня факторной переменной,
-отклонение от среднего, вызванное изменением уровня факторной переменной, 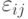 - погрешности с нулевым математическим ожиданием.Контраст
- погрешности с нулевым математическим ожиданием.Контраст 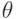 параметров
параметров 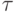 в этой модели задан следующим образом
в этой модели задан следующим образом 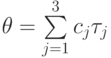 , где
, где 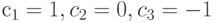 .Определенный таким образом контраст характеризует
.Определенный таким образом контраст характеризует , имеющего 5 градаций, и номинального признака
, имеющего 5 градаций, и номинального признака  , имеющего 4 градации, составлена таблица сопряженности и вычислено значение статистики хи-квадрат. Значение статистики оказалось равным 23.13. Согласно таблицам, квантили распределения хи-квадрат
, имеющего 4 градации, составлена таблица сопряженности и вычислено значение статистики хи-квадрат. Значение статистики оказалось равным 23.13. Согласно таблицам, квантили распределения хи-квадрат  ,
,  .Какой (какие) выводы можно сделать, опираясь на полученный результат?
.Какой (какие) выводы можно сделать, опираясь на полученный результат?  и
и  , измеренных в номинальной шкале, составлена таблица сопряженности 2х2 и вычислен коэффициент контингенции. Этот коэффициент
, измеренных в номинальной шкале, составлена таблица сопряженности 2х2 и вычислен коэффициент контингенции. Этот коэффициент и
и  , измеренных в номинальной шкале, составлена таблица сопряженности и вычислена мера Гутмана
, измеренных в номинальной шкале, составлена таблица сопряженности и вычислена мера Гутмана  . Полученное значение следует трактовать таким образом:
. Полученное значение следует трактовать таким образом:  и
и  измерены в количественной шкале. Требуется выяснить, являются ли эти переменные независимыми. Для того чтобы решить эту задачу, можно
измерены в количественной шкале. Требуется выяснить, являются ли эти переменные независимыми. Для того чтобы решить эту задачу, можно и
и  оказался равным -0.7. Эта информация
оказался равным -0.7. Эта информация 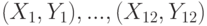 вычислен выборочный коэффициент корреляции
вычислен выборочный коэффициент корреляции 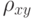 . Какое распределение имеет статистика
. Какое распределение имеет статистика 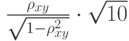 в том случае, когда случайные величины
в том случае, когда случайные величины  и
и  независимы?
независимы? 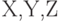 :
: 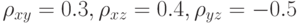 Частный коэффициент корреляции случайных величин
Частный коэффициент корреляции случайных величин  и
и  при фиксированном значении
при фиксированном значении  будет
будет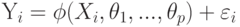 ,
, 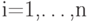 , где
, где 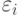 - ненаблюдаемые центрированные погрешности, имеющие плотность распределения
- ненаблюдаемые центрированные погрешности, имеющие плотность распределения 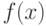 . Для оценивания неизвестных параметров
. Для оценивания неизвестных параметров 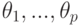 применен метод наименьших модулей (МНМ). Величины дисперсий
применен метод наименьших модулей (МНМ). Величины дисперсий 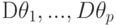 , полученных МНМ-оценок, зависят от
, полученных МНМ-оценок, зависят от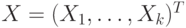 представлен в виде
представлен в виде 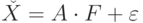 ,где F- вектор общих факторов размерности
,где F- вектор общих факторов размерности  ,
, 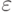 - вектор случайных погрешностей размерности k, А - матрица нагрузок размерности
- вектор случайных погрешностей размерности k, А - матрица нагрузок размерности 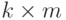 . Элементы
. Элементы 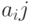 ,
,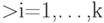
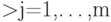 матрицы А - это
матрицы А - это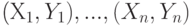 , соответствующей некоторому распределению
, соответствующей некоторому распределению 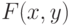 , вычислен выборочный коэффициент корреляции
, вычислен выборочный коэффициент корреляции 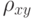 . Объем выборки n известен. Имея эту информацию, можно
. Объем выборки n известен. Имея эту информацию, можно  измерена в номинальной шкале, а переменная
измерена в номинальной шкале, а переменная  - в количественной шкале. Требуется выяснить, являются ли эти переменные независимыми. Для того чтобы решить эту задачу, можно
- в количественной шкале. Требуется выяснить, являются ли эти переменные независимыми. Для того чтобы решить эту задачу, можно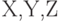 :
:  Частный коэффициент корреляции случайных величин
Частный коэффициент корреляции случайных величин  и
и  при фиксированном значении
при фиксированном значении  будет
будет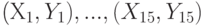 вычислен выборочный коэффициент корреляции
вычислен выборочный коэффициент корреляции 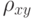 . Какое распределение имеет статистика
. Какое распределение имеет статистика  в том случае, когда случайные величины
в том случае, когда случайные величины  и
и  независимы?
независимы?  измеряется в номинальной шкале и имеет 6 градаций, переменная
измеряется в номинальной шкале и имеет 6 градаций, переменная  измеряется в номинальной шкале и имеет 4 градации. Для того чтобы выяснить, являются ли переменные
измеряется в номинальной шкале и имеет 4 градации. Для того чтобы выяснить, являются ли переменные  и
и  зависимыми, применяют критерий хи-квадрат. Какое число степеней свободы будет иметь статистика хи-квадрат в случае справедливости основной гипотезы?
зависимыми, применяют критерий хи-квадрат. Какое число степеней свободы будет иметь статистика хи-квадрат в случае справедливости основной гипотезы? 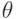 линейной регрессионной модели совпадает с оценкой максимального правдоподобия параметра
линейной регрессионной модели совпадает с оценкой максимального правдоподобия параметра 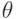
 и
и  , измеренных в номинальной шкале, составлена таблица сопряженности и вычислен коэффициент Крамера
, измеренных в номинальной шкале, составлена таблица сопряженности и вычислен коэффициент Крамера  . Полученный результат можно трактовать следующим образом
. Полученный результат можно трактовать следующим образом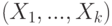 требуется наилучшим образом описать вектором общих факторов
требуется наилучшим образом описать вектором общих факторов 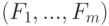 размерности
размерности  . Новые показатели
. Новые показатели 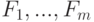 должны удовлетворять следующему условию
должны удовлетворять следующему условию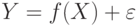 , в которой
, в которой  и
и  – наблюдаемые случайные величины, а
– наблюдаемые случайные величины, а  - ненаблюдаемая случайная помеха с нулевым математическим ожиданием. Предполагается, что случайные величины X и
- ненаблюдаемая случайная помеха с нулевым математическим ожиданием. Предполагается, что случайные величины X и 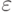 независимы. Корреляционным отношением переменной
независимы. Корреляционным отношением переменной  по
по  называют
называют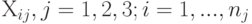 описываются моделью следующего вида
описываются моделью следующего вида  , где
, где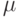 -неизвестное общее среднее,
-неизвестное общее среднее, 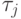 -отклонение от среднего, вызванное изменением уровня факторной переменной,
-отклонение от среднего, вызванное изменением уровня факторной переменной, 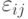 - погрешности с нулевым математическим ожиданием.Контраст
- погрешности с нулевым математическим ожиданием.Контраст 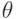 параметров
параметров 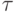 в этой модели задан следующим образом
в этой модели задан следующим образом 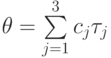 , где
, где 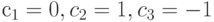 .Определенный таким образом контраст характеризует
.Определенный таким образом контраст характеризует , имеющего 4 градаций, и номинального признака
, имеющего 4 градаций, и номинального признака  , имеющего 6 градации, составлена таблица сопряженности и вычислено значение статистики хи-квадрат. Значение статистики оказалось равным 26.07. Согласно таблицам квантили распределения хи-квадрат
, имеющего 6 градации, составлена таблица сопряженности и вычислено значение статистики хи-квадрат. Значение статистики оказалось равным 26.07. Согласно таблицам квантили распределения хи-квадрат 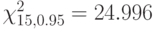 ,
,  .Какой (какие) выводы можно сделать, опираясь на полученный результат?
.Какой (какие) выводы можно сделать, опираясь на полученный результат?  и
и  , измеренных в номинальной шкале, составлена таблица сопряженности и вычислен коэффициент среднеквадратической сопряженности
, измеренных в номинальной шкале, составлена таблица сопряженности и вычислен коэффициент среднеквадратической сопряженности 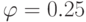 . Полученный результат можно трактовать следующим образом
. Полученный результат можно трактовать следующим образом и
и  , измеренных в номинальной шкале, составлена таблица сопряженности 2х2 и вычислена статистика хи-квадрат. Эта статистика
, измеренных в номинальной шкале, составлена таблица сопряженности 2х2 и вычислена статистика хи-квадрат. Эта статистика экспертов вычислен коэффициент конкордации Кендалла
экспертов вычислен коэффициент конкордации Кендалла 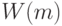 . Значение
. Значение 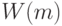 близкое к единице нужно трактовать следующим образом:
близкое к единице нужно трактовать следующим образом: 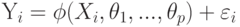 ,
, 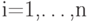 , где
, где 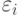 - ненаблюдаемые центрированные погрешности, имеющие плотность распределения
- ненаблюдаемые центрированные погрешности, имеющие плотность распределения 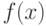 . Для оценивания неизвестных параметров
. Для оценивания неизвестных параметров 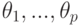 применен метод наименьших квадратов (МНК). Величины дисперсий
применен метод наименьших квадратов (МНК). Величины дисперсий 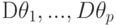 , полученных МНК-оценок, зависят от
, полученных МНК-оценок, зависят от и
и  , измеренных в номинальной шкале, составлена таблица сопряженности и вычислена мера Гутмана
, измеренных в номинальной шкале, составлена таблица сопряженности и вычислена мера Гутмана  . Полученное значение следует трактовать таким образом:
. Полученное значение следует трактовать таким образом:  измеряется в номинальной шкале и имеет 5 градаций, переменная
измеряется в номинальной шкале и имеет 5 градаций, переменная  измеряется в номинальной шкале и имеет 2 градации. Для того чтобы выяснить, являются ли переменные
измеряется в номинальной шкале и имеет 2 градации. Для того чтобы выяснить, являются ли переменные  и
и  зависимыми, применяют критерий хи-квадрат. Какое число степеней свободы будет иметь статистика хи-квадрат в случае справедливости основной гипотезы?
зависимыми, применяют критерий хи-квадрат. Какое число степеней свободы будет иметь статистика хи-квадрат в случае справедливости основной гипотезы?