По двумерной выборке 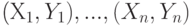 , соответствующей некоторому распределению
, соответствующей некоторому распределению 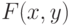 , вычислен выборочный коэффициент корреляции
, вычислен выборочный коэффициент корреляции 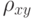 . Объем выборки n известен. Имея эту информацию, можно
. Объем выборки n известен. Имея эту информацию, можно
(Отметьте один правильный вариант ответа.)
Варианты ответа
на заданном уровне значимости проверить гипотезу о некоррелированности случайных величин  и
и  для любого n>3
для любого n>3
 и
и  для любого n>3
для любого n>3
на заданном уровне значимости проверить гипотезу о независимости случайных величин  и
и  для любого n>3
для любого n>3
 и
и  для любого n>3
для любого n>3
на заданном уровне значимости проверить гипотезу о независимости случайных величин  и
и  только при достаточно большом объеме выборки n
только при достаточно большом объеме выборки n
 и
и  только при достаточно большом объеме выборки n
только при достаточно большом объеме выборки n
на заданном уровне значимости проверить гипотезу о некоррелированности случайных величин  и
и  только при достаточно большом объеме выборки n(Верный ответ)
только при достаточно большом объеме выборки n(Верный ответ)
 и
и  только при достаточно большом объеме выборки n(Верный ответ)
только при достаточно большом объеме выборки n(Верный ответ)

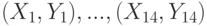 вычислен выборочный коэффициент корреляции
вычислен выборочный коэффициент корреляции 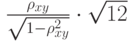 в том случае, когда случайные величины
в том случае, когда случайные величины 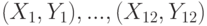 вычислен выборочный коэффициент корреляции
вычислен выборочный коэффициент корреляции 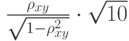 в том случае, когда случайные величины
в том случае, когда случайные величины 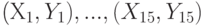 вычислен выборочный коэффициент корреляции
вычислен выборочный коэффициент корреляции  в том случае, когда случайные величины
в том случае, когда случайные величины 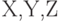 :
:  Частный коэффициент корреляции случайных величин
Частный коэффициент корреляции случайных величин  будет
будет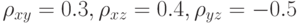 Частный коэффициент корреляции случайных величин
Частный коэффициент корреляции случайных величин 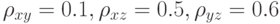 Частный коэффициент корреляции случайных величин
Частный коэффициент корреляции случайных величин 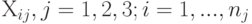 описываются моделью следующего вида
описываются моделью следующего вида  , где
, где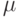 -неизвестное общее среднее,
-неизвестное общее среднее, 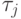 -отклонение от среднего, вызванное изменением уровня факторной переменной,
-отклонение от среднего, вызванное изменением уровня факторной переменной, 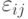 - погрешности с нулевым математическим ожиданием.Контраст
- погрешности с нулевым математическим ожиданием.Контраст 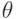 параметров
параметров 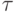 в этой модели задан следующим образом
в этой модели задан следующим образом 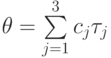 , где
, где 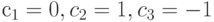 .Определенный таким образом контраст характеризует
.Определенный таким образом контраст характеризует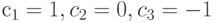 .Определенный таким образом контраст характеризует
.Определенный таким образом контраст характеризует .Определенный таким образом контраст характеризует
.Определенный таким образом контраст характеризует