Чему равна обратная матрица 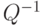 для матрицы
для матрицы  ,
,
(Отметьте один правильный вариант ответа.)
Варианты ответа
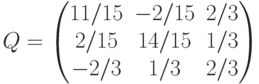
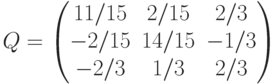 (Верный ответ)
(Верный ответ)

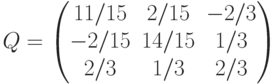
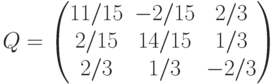
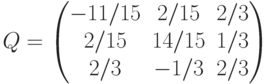
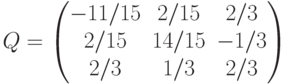
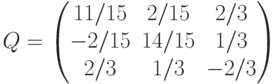

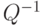 для матрицы
для матрицы  ,
,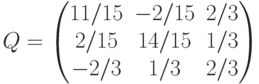
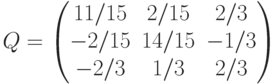 (Верный ответ)
(Верный ответ)

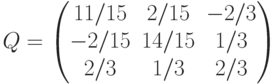
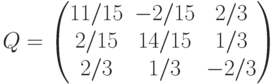
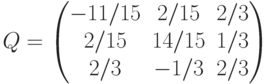
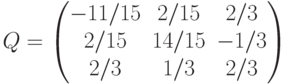
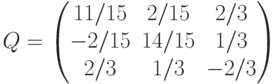
 к базису
к базису 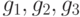 , базисы заданы своими координатами в линейном пространстве
, базисы заданы своими координатами в линейном пространстве 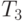 :
:
 ?
? к базису
к базису 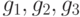 , базисы заданы своими координатами в линейном пространстве
, базисы заданы своими координатами в линейном пространстве 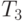 :
:
 ?
? и
и  в каждом из базисов, базисы заданы своими координатами в линейном пространстве
в каждом из базисов, базисы заданы своими координатами в линейном пространстве 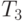 :
:
 ?
?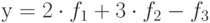 в базисе
в базисе 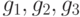 , базисы заданы своими координатами в линейном пространстве
, базисы заданы своими координатами в линейном пространстве 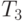 :
:
 ?
?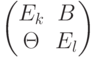 в компьютерной алгебре при условии, что Еk и El — единичные матрицы k-го и l-го порядков, В — произвольная k х l матрица?
в компьютерной алгебре при условии, что Еk и El — единичные матрицы k-го и l-го порядков, В — произвольная k х l матрица? ?
?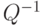 от ортонормированного базиса
от ортонормированного базиса 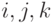 в пространстве
в пространстве 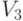 геометрических векторов к базису
геометрических векторов к базису 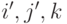 , где векторы
, где векторы  получаются соответственно из векторов
получаются соответственно из векторов  и
и  поворотом их на угол
поворотом их на угол  в плоскости этих векторов?
в плоскости этих векторов?