Введение в компьютерную алгебру - ответы
Количество вопросов - 432
Чему равен наибольший общий делитель многочленов 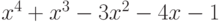 и
и 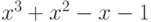 ?
?
Каким методом из приведённых осуществляется вычисление числителя рациональной части интегрируемой функции?
К какому типу относится гомоморфизм разложимый в композицию гомоморфизмов в любом поле?
Чему равны элементы базиса Грёбнера при 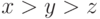 для следующей системы уравнений
для следующей системы уравнений  ?
?
Чему равны члены определителя четвёртого порядка, содержащие элемент  и входящие в определитель со знаком плюс?
и входящие в определитель со знаком плюс?
Чему равен x для следующего равенства $$\begin{vmatrix}3 & x & -4\\2 & -1 & 3\\x + 10 & 1 & 1\end{vmatrix}=0$$ в компьютерной алгебре?
Какой из перечисленных параметров зависит от степени расширения при реализации компьютерных вычислений в полях алгебраических чисел?
Чему равна размерность пространства 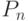 многочленов степени, не превосходящей
многочленов степени, не превосходящей  ?
?
Чему равно число инверсий в перестановке (за исходное расположение принимается расположение 1, 2, 3, ... в возрастающем порядке): 1, 9, 6, 3, 2, 5, 4, 7, 8?
Чему равно  для пространства
для пространства  , которое изоморфно пространству
, которое изоморфно пространству 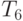 ?
?
Чему равна матрица оператора дифференцирования (оператора  ) в пространстве
) в пространстве  многочленов степени, не превосходящей 2, в базисе
многочленов степени, не превосходящей 2, в базисе 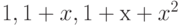 ?
?
Чему равно число инверсий в перестановке  ?
?
Чему равно значение определителя: ?
?
Чему равно разложение на линейные и квадратные множители над полем вещественных чисел многочлена 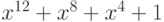 ?
?
Чему равно значение определителя: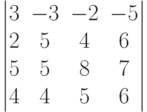 ?
?
Чему равна размерность линейного пространства многочленов 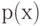 степени не выше
степени не выше  , которые удовлетворяют условию
, которые удовлетворяют условию 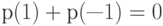 ?
?
Чему равно значение определителя: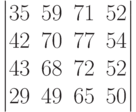 ?
?
В каком из перечисленных полей наряду с арифметическими операциями имеется операция дифференцирования?
Чему равен X для системы линейных уравнений 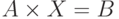 , где
, где  ?
?
Каким количеством способов любая матрица раскладывается в виде суммы симметрической и кососимметрической матриц?
Чему равна размерность линейного пространства R многочленов р(х), степень которых не выше двух и которые удовлетворяют условию р(A) = 0?
Чему равна матрица линейного оператора  в базисе
в базисе 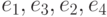 , если матрица данного линейного оператора
, если матрица данного линейного оператора  в базисе
в базисе 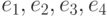 имеет вид:
имеет вид:  ?
?
С каким знаком приведённое ниже произведение входит в определитель соответствующего порядка: 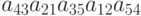 ?
?
Какое количество элементов должны иметь любые два поля чтобы быть изоморфными?
Какие значения принимает определитель унитарной матрицы?
Чему равна обратная матрица для матрицы в компьютерной алгебре?
Чему равен определитель $$\begin{vmatrix}sin^2 \alpha & cos^2 \alpha & cos2\alpha\\sin^2 \beta & cos^2 \beta & cos2\beta\\sin^2 \gamma & cos^2 \gamma & cos2\gamma\end{vmatrix}$$ в компьютерной алгебре?
Чему равна обратная матрица для блочной матрицы 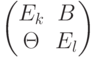 в компьютерной алгебре при условии, что Еk и El — единичные матрицы k-го и l-го порядков, В — произвольная k х l матрица?
в компьютерной алгебре при условии, что Еk и El — единичные матрицы k-го и l-го порядков, В — произвольная k х l матрица?
Какие значения принимает определитель ортогональной матрицы?
Какой след имеет нильпонентная матрица порядка два?
Чему равно наибольшее значение определителя третьего порядка составленного из нулей и единиц?
Каким будет результат от возведения в степень n матрицы в компьютерной алгебре?
Для любых матриц какого порядка выполняется равенство в компьютерной алгебре?
Элемент какого порядка содержится во всякой группе чётного порядка?
Чему равен порядок единицы поля в его аддитивной группе?
Чему равна размерность пространства 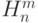 матриц с размерами
матриц с размерами  ?
?
Чему равна размерность пространства симметричных  - матриц?
- матриц?
Чему равна размерность пространства многочленов р(х) из 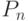 , удовлетворяющих условию
, удовлетворяющих условию 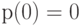 ?
?
Чему равно максимальное число линейно независимых столбцов в системе столбцов  ?
?
Чему равно максимальное число линейно независимых столбцов в системе столбцов 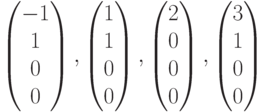 ?
?
Чему равен ранг матрицы  ?
?
Чему равен ранг матрицы 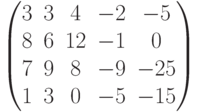 ?
?
Чему равен ранг матрицы  ?
?
Чему равна размерность линейной оболочки элементов, заданных столбцами своих координат в некотором базисе линейного пространства: ?
?
Чему равна размерность линейного пространства столбцов с  элементами
элементами 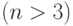 , у которых сумма первых трех элементов равна нулю?
, у которых сумма первых трех элементов равна нулю?
Чему равна размерность линейного пространства многочленов 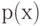 степени не выше 4, которые удовлетворяют условию
степени не выше 4, которые удовлетворяют условию 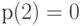 ?
?
Чему равны координаты элемента 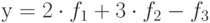 в базисе
в базисе 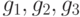 , базисы заданы своими координатами в линейном пространстве
, базисы заданы своими координатами в линейном пространстве 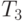 :
:
 ?
?
Чему равно разложение элемента 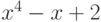 пространства
пространства 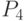 по базису
по базису 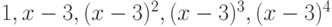 ?
?
Чему равна матрица обратного перехода от базиса  к базису
к базису 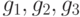 , где
, где 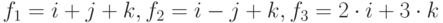 ,
,  ?
?
Чему равно  для пространства симметричных
для пространства симметричных  - матриц с нулевыми диагональными элементами, которое изоморфно пространству
- матриц с нулевыми диагональными элементами, которое изоморфно пространству 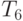 ?
?
Чему равно  для подпространства столбцов из
для подпространства столбцов из 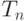 , сумма элементов которых равна нулю, которое изоморфно пространству
, сумма элементов которых равна нулю, которое изоморфно пространству 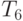 ?
?
При каких значениях  совместна система уравнений
совместна система уравнений  ?
?
Чему равна размерность подпространства элементов из  каждый из которых ортогонален к данным элементам
каждый из которых ортогонален к данным элементам 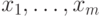
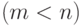 ?
?
Чему равен базис ортогонального дополнения к пространству решений однородной системы линейных уравнений:  ?
?
Чему равны элементы решений следующей системы уравнений  ?
?
Чему равны все подстановки чисел 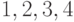 , перестановочные с подстановкой
, перестановочные с подстановкой 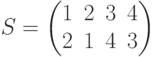 ?
?
Чему равны элементы решений следующей системы уравнений 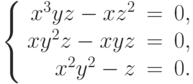 ?
?
Чему равны элементы базиса Грёбнера при 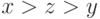 для следующей системы уравнений
для следующей системы уравнений  ?
?
Какаие из перечисленных вариантов реализуют интегрирование рациональных функций с действительными коэффициентами?
Чему равен ранг матрицы при различных значениях в компьютерной алгебре?
Чему равна матрица перехода от базиса  к базису
к базису 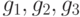 , базисы заданы своими координатами в линейном пространстве
, базисы заданы своими координатами в линейном пространстве 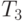 :
:
 ?
?
Чему равна матрица обратного перехода 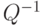 от ортонормированного базиса
от ортонормированного базиса 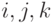 в пространстве
в пространстве 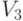 геометрических векторов к базису
геометрических векторов к базису 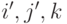 , где векторы
, где векторы  получаются соответственно из векторов
получаются соответственно из векторов  и
и  поворотом их на угол
поворотом их на угол  в плоскости этих векторов?
в плоскости этих векторов?
Чему равна обратная матрица 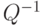 для матрицы
для матрицы  ,
,
Чему равна матрица оператора дифференцирования (оператора  ) в пространстве
) в пространстве  многочленов степени, не превосходящей 2, в базисе
многочленов степени, не превосходящей 2, в базисе  ?
?
Чему равна матрица линейного оператора  в базисе
в базисе 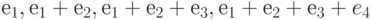 , если матрица данного линейного оператора
, если матрица данного линейного оператора  в базисе
в базисе 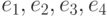 имеет вид:
имеет вид:  ?
?
На какое число необходимо умножить определитель  -го порядка, если его строки записать в обратном порядке?
-го порядка, если его строки записать в обратном порядке?
На какое число необходимо умножить определитель, если у всех его элементов изменить знак на противоположный?
На какое число необходимо умножить определитель порядка n, если его матрицу повернуть на 90 градусов вокруг "центра"?
Чему равна сумма всех определителей порядка  , в каждом из которых в каждой строке и каждом столбце один элемент равен единице, а остальные равны нулю?
, в каждом из которых в каждой строке и каждом столбце один элемент равен единице, а остальные равны нулю?
Чему равен определитель порядка  , элементы которого заданы условиями
, элементы которого заданы условиями  ?
?
Чему равен определитель порядка  , элементы которого заданы условиями
, элементы которого заданы условиями 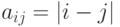 ?
?
Чему равен x, y, z для данных уравнений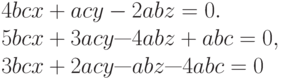 ,где
,где  ?
?
Чему равно число инверсий в перестановке (за исходное расположение принимается расположение 1, 2, 3, ... в возрастающем порядке): 2, 3, 5, 4, 1?
Чему равно число инверсий в перестановке (за исходное расположение принимается расположение 1, 2, 3, ... в возрастающем порядке): 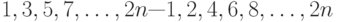 ?
?
Чему равно число инверсий в перестановке (за исходное расположение принимается расположение 1, 2, 3, ... в возрастающем порядке): 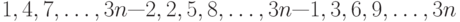 ?
?
При каких значениях  перестановка:
перестановка: 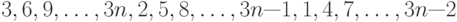 нечётна?
нечётна?
Чему равно число инверсий в перестановке (за исходное расположение принимается расположение 1, 2, 3, ... в возрастающем порядке): 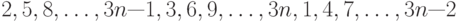 ?
?
При каких значениях  перестановка:
перестановка: 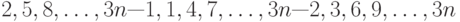 чётна?
чётна?
Чему равно число инверсий в перестановке (за исходное расположение принимается расположение 1, 2, 3, ... в возрастающем порядке): 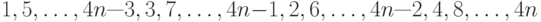 ?
?
При каких значениях  перестановка: ):
перестановка: ):  чётна?
чётна?
Чему равна сумма числа инверсий и числа порядков в любой перестановке чисел  ?
?
Для каких чисел  четность числа инверсий и числа порядков во всех перестановках чисел
четность числа инверсий и числа порядков во всех перестановках чисел  противоположна?
противоположна?
Чему равен декремент подстановки 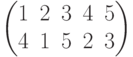 ?
?
Чему равно разложение в произведение независимых циклов подстановки  ?
?
Чему равно разложение в произведение независимых циклов подстановки 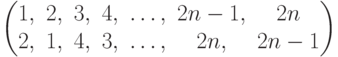 ?
?
Чему равно разложение в произведение независимых циклов подстановки 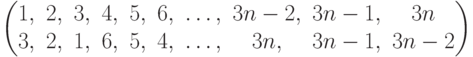 ?
?
Чему равен декремент подстановки 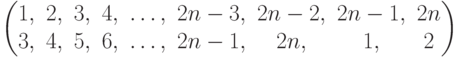 ?
?
Чему равно разложение в произведение независимых циклов подстановки 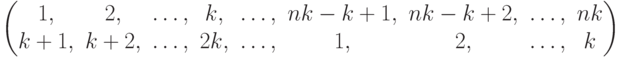 ?
?
Чему равно  , где
, где 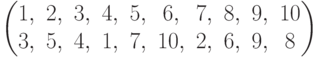 ?
?
Чему равны все подстановки чисел 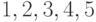 , перестановочные с подстановкой
, перестановочные с подстановкой  ?
?
С каким знаком приведённое ниже произведение входит в определитель соответствующего порядка: 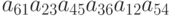 ?
?
С каким знаком приведённое ниже произведение входит в определитель соответствующего порядка: 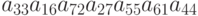 ?
?
С каким знаком приведённое ниже произведение входит в определитель соответствующего порядка: 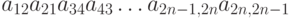 ?
?
Чему равны значения  и
и  такие, что произведение
такие, что произведение 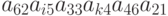 входили бы в определитель 6-го порядка со знаком минус?
входили бы в определитель 6-го порядка со знаком минус?
Чему равно значение определителя: ?
?
Чему равно значение определителя: ?
?
Чему равно значение определителя: ?
?
Чему равно значение определителя: ?
?
Чему равно значение определителя: ?
?
Сколько миноров  -го порядка содержит определитель порядка
-го порядка содержит определитель порядка  ?
?
Чему равна кратность корня 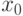 многочлена
многочлена  , где
, где  ,
, 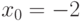 ?
?
Чему равна сумма чисел, обратных комплексным корням многочлена: 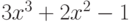 ?
?
Чему равна сумма чисел, обратных комплексным корням многочлена: 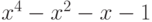 ?
?
Чему равен наибольший общий делитель многочленов: 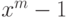 и
и  ?
?
Чему равен многочлен степени четыре со старшим коэффициентом один имеющий корни 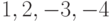 ?
?
Чему равна сумма квадратов и произведение всех комплексных корней многочлена: 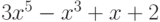 ?
?
Чему равна сумма квадратов и произведение всех комплексных корней многочлена: 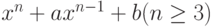 ?
?
Чему равен наибольший общий делитель многочленов 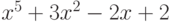 и
и  ?
?
Чему равно линейное выражение наибольшего общего делителя многочленов  и
и 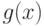 через
через  и
и 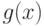 , где
, где  ,
, 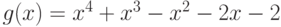 ?
?
Найдите рациональный корень уравнения 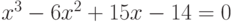 ?
?
Чему равны все рациональные корни многочлена 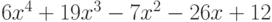 ?
?
Чему равен результат деления многочлена  на
на  , если
, если 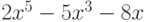 и
и 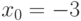 ?
?
Чему равно значение  , если
, если  и
и 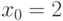 ?
?
Чему равно значение  , если
, если  и
и 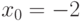 ?
?
Чему равно значение производной 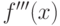 в точке 2, если
в точке 2, если  ?
?
Чему равно значение производной  в точке 2, если
в точке 2, если 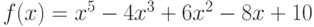 ?
?
Чему равно значение производной 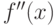 в точке 2, если
в точке 2, если 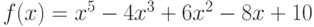 ?
?
Чему равно разложение на линейные и квадратные множители над полем вещественных чисел многочлена  ?
?
Чему равно разложение на линейные и квадратные множители над полем вещественных чисел многочлена 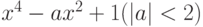 ?
?
Чему равен многочлен наименьшей степени с вещественными коэффициентами, имеющий двойной корень  , простой корень
, простой корень 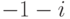 ?
?
Чему равен набор степеней старшего члена многочлена, многоугольник Ньютона которого указан на рисунке?
Чему равно число вершин многогранника Ньютона многочлена  ?
?
Чему равен минимальный редуцированный базис Грёбнера для идеала 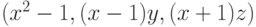 , где
, где 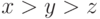 ?
?
Чему равен минимальный редуцированный базис Грёбнера для идеала  , где
, где 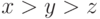 ?
?
Чему равен минимальный редуцированный базис Грёбнера для идеала 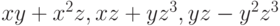 , где
, где 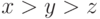 ?
?
Чему равны элементы базиса Грёбнера при 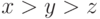 для следующей системы уравнений
для следующей системы уравнений  ?
?
Чему равны элементы базиса Грёбнера при 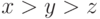 для следующей системы уравнений
для следующей системы уравнений 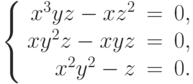 ?
?
Чему равны элементы базиса Грёбнера при 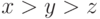 для следующей системы уравнений
для следующей системы уравнений  ?
?
Чему равны элементы решений следующей системы уравнений  ?
?
Чему равны элементы решений следующей системы уравнений  ?
?
Чему равно число уравнений заданное тремя токами 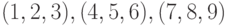 в множестве
в множестве  ?
?
Для каких чисел реализуем алгоритм выделения неприводимого множителя при использовании редуцированного базиса решетки?
Для каких чисел ограничена степень неприводимого множителя при реализации алгоритма факторизации, основанного на выборе малого вектора в решетке?
Какой алгоритм из приведённых ниже позволяет найти минимальный вектор решетки?
Каким приближением из приведённых ниже необходимо воспользоваться для нахождения неприводимого множителя с заданной точностью?
Какой из приведенных ниже этапов относится к этапам поиска неприводимого множителя с заданной точностью?
Для какого поля реализован алгоритм факторизации при использовании архимедовой метрики?
Какая из приведённых ниже метрик используется в качестве метрики в алгоритме факторизации поля комплексных чисел K определённом над полем Q?
К какому типу относится неприводимый многочлен в алгоритме факторизации при реализации архимедовой метрики на поле Q в комплексном случае?
В каком поле линейный неприводимый многочлен нормирован?
В каком поле решетка совпадает с Z-модулем всех многочленов с целыми коэффициентами, не превышающими ранг решетки?
К какому типу из перечисленных ниже относится множитель разложимый в ряд Тейлора в любом поле?
Как называется уравнение вида  ?
?
Решением какого уравнения является первообразная функции  ?
?
Для каких коэффициентов класс функций порождённый функцией f(x) уравнения 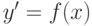 является полем рациональных функций от одной переменной?
является полем рациональных функций от одной переменной?
В какой ряд из перечисленных разложима функция  в любом поле, если данная функция входит в уравнение вида
в любом поле, если данная функция входит в уравнение вида 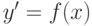 ?
?
К какому типу функций относится функция интегрируемая без алгебраического расширения поля констант?
При помощи каких из перечисленных ниже математических конструкций осуществляется интегрирование рациональных функций с действительными коэффициентами?
С какими аргументами выражаются через логарифмы арктангенсы при интегрировании рациональных функций с действительными коэффициентами?
В каких коэффициентах представима рациональная функция в виде суммы полинома и правильной дроби?
К какой из приведённых математических конструкций относится интеграл от полиномиальной функции?
Какой дробью является сумма правильных дробей знаменатели которых являются неприводимыми полиномами?
Через какую математическую конструкцию определяется дифференцирование в полях?
В каком из перечисленных полей определена независимая переменная над вычислимым полем констант?
В каком поле интегрируема функция принадлежащая полю элементарных функций?
Какой из перечисленных интегралов определён, если определен интеграл элементарной логарифмической функции и интеграл полиномиальной части логарифмической функции?
В каком поле определено понижение степени полинома при дифференцировании больше, чем на единицу?
Как называется регулярный моном определённый над полем, которому принадлежит его правая часть?
Каким из перечисленных методов определено интегрирование полиномиальной части функции в любом поле?
Какая из перечисленных констант является константой интегрирования?
Какой из приведенных этапов относится к этапам интегрирования правильной рациональной функции?
Какой из перечисленных интегралов определён, если определен интеграл полиномиальной части экспоненциальной функции и интеграл рациональной части экспоненциальной функции?
В каком из перечисленных колец уравнения Риша являются квадратными?
На какую величину из перечисленных изменяется степень полинома при дифференцировании по x полинома от экспоненты со старшим коэффициентом 1?
В виде суммы каких математических объектов представлен результат интегрирования согласно принципу Лиувилля?
К какому типу относятся многочлены разложимые в ряд Тейлора неприводимого множителя в поле комплексных чисел?
Чем отличаются между собой понятия неопределенный интеграл функции и первообразная функции?
Чему равен элемент определителя порядка  , симметричный элементу
, симметричный элементу 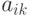 относительно "центра" определителя?
относительно "центра" определителя?
С каким знаком приведённое ниже произведение входит в определитель соответствующего порядка: 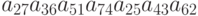 ?
?
Какая из приведённых функций разложима в ряд Лорана, если данная функция входит в уравнение вида 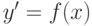 ?
?
Чему равно значение  , если
, если 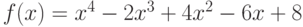 и
и  ?
?
Чему равны координаты вектора х в базисе 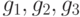 , где
, где  ,
, 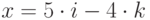 ?
?
Чему равна размерность линейной оболочки элементов, заданных столбцами своих координат в некотором базисе линейного пространства:  ?
?
Чему равно значение определителя: ?
?
Чему равна размерность линейного пространства симметричных 3 х 3 - матриц?
Чему равен многочлен наименьшей степени с комплексными коэффициентами, имеющий двойной корень  , простой корень
, простой корень 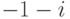
Чему равны элементы решений следующей системы уравнений  ?
?
Чему равно значение производной  в точке 2, если
в точке 2, если  ?
?
Чему равно значение определителя: ?
?
В каком кольце функция, принадлежащая полю рациональных чисел, разложима в сумму полинома и правильной рациональной дроби?
При каких значениях  перестановка:
перестановка:  чётна?
чётна?
Для каких чисел ограничена степень неприводимого множителя?
Какие из приведённых ниже метрик реализованы при использовании алгоритма факторизации?
Для какой функции из приведённых релизовано раздельное интегрирование полиномиальной и рациональной части?
Чему равна матрица обратного перехода 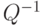 от ортонормированного базиса
от ортонормированного базиса 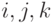 в пространстве
в пространстве 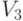 геометрических векторов к базису
геометрических векторов к базису 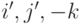 , где векторы
, где векторы  получаются соответственно из векторов
получаются соответственно из векторов  и
и  поворотом их на угол
поворотом их на угол  в плоскости этих векторов?
в плоскости этих векторов?
С каким знаком приведённое ниже произведение входит в определитель соответствующего порядка: 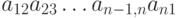 ?
?
Чему равен декремент подстановки 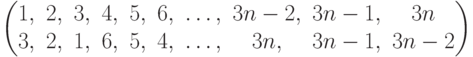 ?
?
При каких значениях  перестановка:
перестановка: 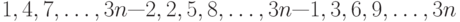 нечётна?
нечётна?
Чему равно число инверсий в перестановке (за исходное расположение принимается расположение 1, 2, 3, ... в возрастающем порядке): 7, 5, 6, 4, 1, 3, 2?
Какая операция позволяет найти неприводимый множитель с заданной точностью?
Чему равно значение производной 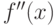 в точке 2, если
в точке 2, если  ?
?
Чему равен наибольший общий делитель многочленов:  и
и  ?
?
Чему равна размерность линейной оболочки элементов, заданных столбцами своих координат в некотором базисе линейного пространства: 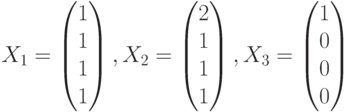 ?
?
Чему равно линейное выражение наибольшего общего делителя многочленов  и
и 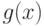 через
через  и
и 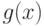 , где
, где 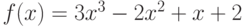 ,
, 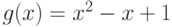 ?
?
Чему равно число инверсий в перестановке (за исходное расположение принимается расположение 1, 2, 3, ... в возрастающем порядке): 6, 3, 1, 2, 5, 4?
Как называется кольцо, в котором определён оператор дифференцирования?
Для каких чисел норма многочлена связана с обычной евклидовой нормой в пространстве многочленов?
Чему равна матрица X, удовлетворяющая уравнению в компьютерной алгебре?
Чему равен определитель матрицы в компьютерной алгебре?
Чему равен x для следующего равенства $$\begin{vmatrix}1 & 0 & x\\0 & x & -1\\x & 8 & 0\end{vmatrix}=0$$ в компьютерной алгебре?
C каким знаком входит в развёрнутое выражение определителя порядка n произведение элементов побочной диагонали?
Чему равно наибольшее значение определителя третьего порядка составленного из единиц и "минус единиц"?
Каким будет результат от возведения в степень n матрицы в компьютерной алгебре?
Делителем какого из перечисленных элементов не является обратимая матрица в кольце матриц над полем?
Какому из перечисленных колец изоморфно кольцо эндоморфизмов циклической группы порядка n?
Какому из приведённых чисел в тригонометрической форме равно число пять?
Чему равна размерность пространства столбцов с n элементами, сумма которых(элементов) равна нулю?
Чему равно максимальное число линейно независимых столбцов в системе столбцов  ?
?
Чему равно максимальное число линейно независимых столбцов в системе столбцов 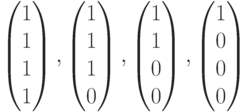 ?
?
Чему равен ранг матрицы 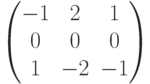 ?
?
Чему равен ранг матрицы  ?
?
Чему равно  для пространства для пространства
для пространства для пространства 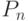 , которое изоморфно пространству
, которое изоморфно пространству 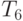 ?
?
Чему равно  для подпространства многочленов
для подпространства многочленов 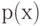 из
из 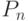 , удовлетворяющих условию
, удовлетворяющих условию 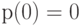 , которое изоморфно пространству
, которое изоморфно пространству 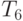 ?
?
При каких значениях  совместна система уравнений
совместна система уравнений 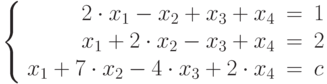 ?
?
Чему равен X для системы линейных уравнений 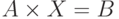 , где
, где  ?
?
Чему равен базис ортогонального дополнения к пространству решений однородной системы линейных уравнений:  ?
?
Чему равна матрица оператора 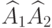 , где
, где 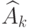 - оператор поворота на угол
- оператор поворота на угол 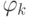 в пространстве
в пространстве 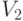 векторов на плоскости?
векторов на плоскости?
Чему равна матрица линейного оператора  в правом ортонормированном базисе
в правом ортонормированном базисе 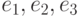 , если
, если 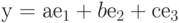 (а, b, с — заданные числа); у — фиксированный вектор линейного пространства
(а, b, с — заданные числа); у — фиксированный вектор линейного пространства 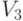 ,
,  — оператор, действие которого на любой вектор
— оператор, действие которого на любой вектор  из
из 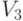 задается равенством
задается равенством ![\widehat А х = [х , у], где [х , у]](https://intuit.ru//sites/default/files/tex_cache/bb53811acdf9d1592baa14383e89273e.png) — векторное произведение вектора
— векторное произведение вектора  на вектор
на вектор  ?
?
На какое число необходимо умножить определитель  -го порядка, если первый столбец переставить на последнее место, а остальные столбцы передвинуть влево, сохраняя их расположение
-го порядка, если первый столбец переставить на последнее место, а остальные столбцы передвинуть влево, сохраняя их расположение
На какое число необходимо умножить определитель, если каждый его элемент заменить элементом, симметричным с данным относительно побочной диагонали?
На какое число необходимо умножить определитель, если каждый его элемент 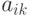 умножить на
умножить на 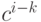 , где
, где 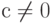 ?
?
На какое число необходимо умножить определитель порядка  , если из каждой строки, кроме последней, вычесть последующую строку, из последней строки вычесть прежнюю первую строку?
, если из каждой строки, кроме последней, вычесть последующую строку, из последней строки вычесть прежнюю первую строку?
Чему равен определитель порядка  , элементы которого заданы условиями
, элементы которого заданы условиями  ?
?
Чему равен x, y, z для данных уравнений , где
, где 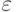 - отличное от 1 значение
- отличное от 1 значение ![$$\sqrt[3]{1}$$](https://intuit.ru//sites/default/files/tex_cache/d7e92ee6f71277afee742de9f299074f.png)
При каких значениях  перестановка:
перестановка: 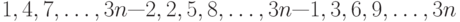 чётна?
чётна?
При каких значениях  перестановка:
перестановка: 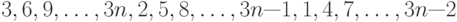 чётна?
чётна?
При каких значениях  перестановка:
перестановка: 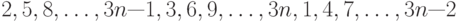 нечётна?
нечётна?
При каких значениях  перестановка:
перестановка: 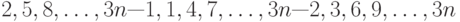 нечётна?
нечётна?
Чему равно число инверсий в перестановке (за исходное расположение принимается расположение 1, 2, 3, ... в возрастающем порядке):  ?
?
Для каких чисел  четность числа инверсий и числа порядков во всех перестановках чисел
четность числа инверсий и числа порядков во всех перестановках чисел  одинакова?
одинакова?
Чему равно разложение в произведение независимых циклов подстановки 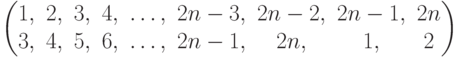 ?
?
Чему равно разложение в произведение независимых циклов подстановки 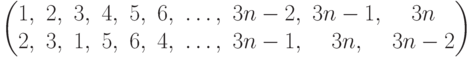 ?
?
Чему равна подстановка  из равенства
из равенства 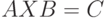 , где
, где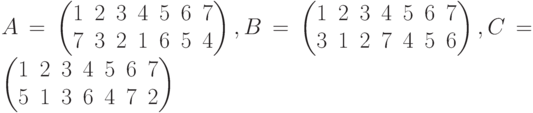 ?
?
Чему равны значения  и
и  такие, что произведение
такие, что произведение 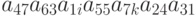 входили бы в определитель 7-го порядка со знаком плюс?
входили бы в определитель 7-го порядка со знаком плюс?
С каким знаком входит в определитель порядка  произведение элементов побочной диагонали?
произведение элементов побочной диагонали?
Чему равно значение определителя: ?
?
Чему равно значение определителя: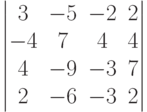 ?
?
Чему равно значение определителя: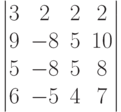 ?
?
Чему равна кратность корня 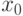 многочлена
многочлена  , где
, где  ,
, 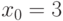 ?
?
При каких  и
и  многочлен
многочлен  делится на
делится на  ?
?
Чему равен многочлен степени четыре со старшим коэффициентом один имеющий тройной корень -1 и простой корень  ?
?
Чему равен наибольший общий делитель многочленов 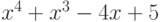 и
и 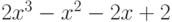 ?
?
Чему равно разложение на неприводимые множители многочлена при помощи выделения его кратных неприводимых множителей 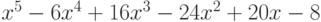 ?
?
Чему равны все рациональные корни многочлена  ?
?
Чему равно значение производной 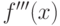 в точке 2, если
в точке 2, если 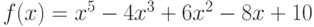 ?
?
Чему равно разложение на линейные и квадратные множители над полем вещественных чисел многочлена 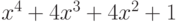 ?
?
Чему равно разложение на линейные и квадратные множители над полем вещественных чисел многочлена 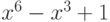 ?
?
Чему равно число граней многогранника Ньютона многочлена  ?
?
Когда набор многочленов 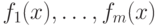 является базисом Грёбнера порожденного ими идеала в K[x]?
является базисом Грёбнера порожденного ими идеала в K[x]?
Чему равны элементы решений следующей системы уравнений  ?
?
Чему равны элементы решений следующей системы уравнений  ?
?
Чему равны элементы базиса Грёбнера при 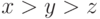 для следующей системы уравнений
для следующей системы уравнений  ?
?
Какой из приведенных этапов относится к этапам алгоритма факторизации, основанного на выборе малого вектора в решетке?
Каким числом ограничена сверху степень неприводимого множителя?
Какое из приведённых ниже полей используется в качестве поля K в алгоритме факторизации при реализации архимедовой метрики на поле Q?
Какая из приведённых ниже метрик используется в качестве метрики для неприводимого многочлена в алгоритме факторизации на поле Q в комплексном случае?
К какому типу относится нормированный неприводимый многочлен?
Как называется результат решения уравнения вида 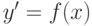 ?
?
В каком из перечисленных полей класс функций порождённый функцией  уравнения
уравнения 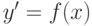 является кольцом полиномов?
является кольцом полиномов?
С помощью какой из приведённых ниже математических конструкций рациональная функция с действительными коэффициентами интегрируется?
Какая из математических конструкции выражается через логарифмы при интегрировании рациональных функций с действительными коэффициентами?
Какая переменная определена в любом поле над вычислимым полем констант?
В каком поле функция, принадлежащая полю рациональных чисел, разложима в сумму полинома и правильной рациональной дроби?
В каком поле при интегрировании полиномиальной части функции в вычислениях не используется константа интегрирования?
Как называется моном трансцендентный над полем, которому принадлежит его правая часть?
Интегрирование какой из перечисленных частей функции определено методом неопределенных коэффициентов?
В каком поле аддитивная константа является константой интегрирования?
Какому из приведённых чисел равны старшие коэффициенты полиномов расположенные в знаменателе функций, которые составляют сумму простейших дробей, на которые разложима данная функция?
С помощью какого из перечисленных методов производится определение числителя рациональной части интеграла?
К какому типу уравнений относятся уравнения Риша?
Чему равен наибольший общий делитель многочленов:  и
и  ?
?
Чему равно разложение многочлена  по степеням
по степеням 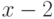 , если
, если  ?
?
В какой перестановке чисел  число инверсий наибольшее?
число инверсий наибольшее?
Чему равно число инверсий в перестановке (за исходное расположение принимается расположение 1, 2, 3, ... в возрастающем порядке): 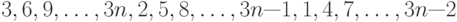 ?
?
С каким знаком приведённое ниже произведение входит в определитель соответствующего порядка: 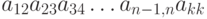 , где
, где 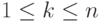 ?
?
Чему равно значение производной  в точке 2, если
в точке 2, если 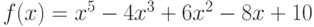 ?
?
Чему равна кратность корня 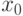 многочлена
многочлена  , где
, где 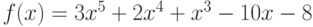 ,
, 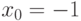 ?
?
Чему равно значение определителя: ?
?
Чему равна сумма и произведение всех комплексных корней степени  из единицы?
из единицы?
Чему равна матрица Q перехода от ортонормированного базиса 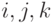 в пространстве
в пространстве 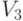 геометрических векторов к базису
геометрических векторов к базису 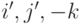 , где векторы
, где векторы  получаются соответственно из векторов
получаются соответственно из векторов  и
и  поворотом их на угол
поворотом их на угол  в плоскости этих векторов?
в плоскости этих векторов?
Чему равен ранг матрицы 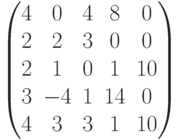 ?
?
Чему равно наибольшее значение, которое может принимать определитель третьего порядка, при условии, что все его элементы равны  ?
?
Чему равна матрица переходов от базиса  к базису
к базису 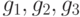 , где
, где 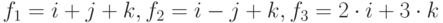 ,
,  ?
?
Чему равны элементы базиса Грёбнера при  для следующей системы уравнений
для следующей системы уравнений  ?
?
При каких значениях  перестановка: ):
перестановка: ): 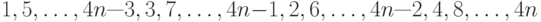 чётна?
чётна?
Чему равны все дифференцирования(D) кольца ?
Для каких чисел реализуется задача факторизации с помощью выделения неприводимого в Z[x] делителя многочлена f(x) для произвольной решетки?
Чему равны координаты элементов  и
и  в каждом из базисов, базисы заданы своими координатами в линейном пространстве
в каждом из базисов, базисы заданы своими координатами в линейном пространстве 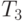 :
:
 ?
?
Чему равно разложение в произведение независимых циклов подстановки  ?
?
При каком значении а многочлен 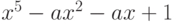 имеет -1 корнем не ниже второй кратности?
имеет -1 корнем не ниже второй кратности?
К какому типу относится линейный неприводимый многочлен?
Чему равен определитель матрицы в компьютерной алгебре?
Сколько элементов содержит полугруппа, состоящая из всех степеней матрицы ?
Чему равен определитель кососимметрической матрицы нечётного порядка?
Каким будет результат выражение , где ? в компьютерной алгебре?
Группе обратимых элементов какого кольца изоморфна группа автоморфизмов циклической группы порядка n?
Какое количество одномерных подпространств содержится в векторном пространстве ?
Чему равно максимальное число линейно независимых столбцов в системе столбцов 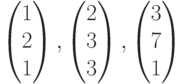 ?
?
Чему равен ранг матрицы 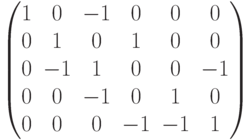 ?
?
Чему равен X для системы линейных уравнений 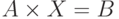 , где
, где 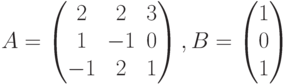 ?
?
Чему равно число определителей порядка  , в каждом из которых в каждой строке и каждом столбце один элемент равен единице, а остальные равны нулю?
, в каждом из которых в каждой строке и каждом столбце один элемент равен единице, а остальные равны нулю?
Чему равно наибольшее значение определителя третьего порядка при условии, что его элементы равны +1 или 0?
Чему равно число инверсий в перестановке (за исходное расположение принимается расположение 1, 2, 3, ... в возрастающем порядке): 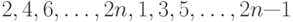 ?
?
Сколько инверсий образует число  , стоящее на
, стоящее на  -м месте в перестановке чисел
-м месте в перестановке чисел 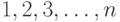 ?
?
Чему равно разложение в произведение независимых циклов подстановки  ?
?
Чему равно разложение в произведение независимых циклов подстановки 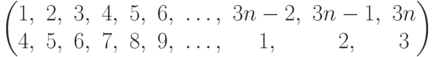 ?
?
Чему равен декремент подстановки 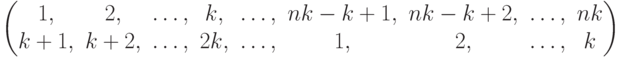 ?
?
Чему равна подстановка чисел 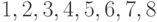 , при которой число
, при которой число  переходит в остаток от деления
переходит в остаток от деления 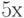 на
на 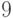 ?
?
С каким знаком входит в определитель порядка  произведение элементов главной диагонали?
произведение элементов главной диагонали?
Чему равно значение определителя: ?
?
Чему равно значение определителя: ?
?
Чему равны все рациональные корни многочлена  ?
?
Чему равен результат деления многочлена  на
на  , если
, если  и
и 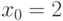 ?
?
Чему равно значение производной  в точке 2, если
в точке 2, если  ?
?
Чему равно разложение многочлена  по степеням
по степеням 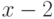 , если
, если 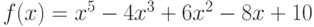 ?
?
Чему равен многочлен наименьшей степени с вещественными коэффициентами, имеющий двойной корень единица, простые корни два, три и  ?
?
Чему равен минимальный редуцированный базис Грёбнера для идеала 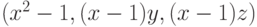 , где
, где 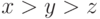 ?
?
Чему равен минимальный редуцированный базис Грёбнера для идеала 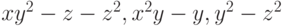 , где
, где 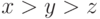 ?
?
Чему равны элементы базиса Грёбнера при  для следующей системы уравнений
для следующей системы уравнений  ?
?
Чему равны элементы решений следующей системы уравнений  ?
?
Какие подмножества плотны в C?
Для каких чисел выделим неприводимый делитель в Z[x] многочлена f(x) для произвольной решетки?
Для какого поля степень неприводимого множителя ограничена сверху натуральным числом?
В каком поле неприводимый множитель разложим в ряд Тейлора?
В каком поле кольцевой гомоморфизм разложим в композицию гомоморфизмов?
К какому типу чисел из перечисленных относятся коэффициенты рациональных функций интегрируемых без алгебраического расширения поля констант?
В каких коэффициентах релизовано раздельное интегрирование полиномиальной и рациональной части произвольной функции?
Для каких коэффициентов определена константа интегрирования при интегрировании полиномиальной части функции?
Константой какого из перечисленных методов является аддитивная константа в любом поле?
На какие множители разложим знаменатель рациональной части интеграла при интегрировании рациональных функций с постоянными коэффициентами?
Как называется алгоритм интегрирования в конечном виде функций из трансцендентного расширения поля рациональных функций, порожденных экспонентами и логарифмами?
В каком поле функция  разложима в ряд Лорана, если данная функция входит в уравнение вида
разложима в ряд Лорана, если данная функция входит в уравнение вида 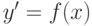 ?
?
Чему равна размерность линейного пространства симметричных 3 х 3 - матриц, диагональные элементы которых равны нулю?
) Чему равен декремент подстановки  ?
?
Чему равен определитель целочисленной матрицы A, если определитель матрицы также целочисленный?
Какой из приведенных этапов относится к этапам алгоритма интегрирования трансцендентных функций?
Чему равна матрица Q перехода от ортонормированного базиса 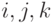 в пространстве
в пространстве 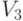 геометрических векторов к базису
геометрических векторов к базису 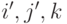 , где векторы
, где векторы  получаются соответственно из векторов
получаются соответственно из векторов  и
и  поворотом их на угол
поворотом их на угол  в плоскости этих векторов?
в плоскости этих векторов?
На какое число необходимо умножить определитель порядка  , у которого сумма строк с четными номерами равна сумме строк с нечетными номерами?
, у которого сумма строк с четными номерами равна сумме строк с нечетными номерами?
При каких m многочлен 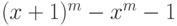 делится на
делится на 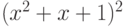 ?
?
Какой из перечисленных интегралов определён, если определен интеграл полиномиальной части логарифмической функции и интеграл рациональной части логарифмической функции?
При каких значениях  перестановка:
перестановка: 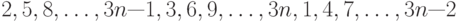 чётна?
чётна?
Чему равен декремент подстановки 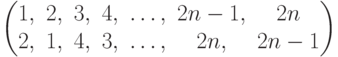 ?
?
Чему равно число инверсий в перестановке (за исходное расположение принимается расположение 1, 2, 3, ... в возрастающем порядке):  ?
?
Чему равна матрица обратного перехода от базиса  к базису
к базису 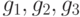 , базисы заданы своими координатами в линейном пространстве
, базисы заданы своими координатами в линейном пространстве 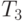 :
:
 ?
?
При каком из перечисленных условий однородная система линейных уравнений имеет ненулевое решение?
Чему равен ранг матрицы  ?
?
Чему равна матрица оператора дифференцирования, действующего в  , в базисе
, в базисе  , где
, где  - линейная оболочка функций
- линейная оболочка функций  ?
?
На какое число необходимо умножить определитель  -го порядка, если каждый его элемент заменить элементом, симметричным с данным относительно "центра" определителя?
-го порядка, если каждый его элемент заменить элементом, симметричным с данным относительно "центра" определителя?
Чему равно число инверсий в перестановке (за исходное расположение принимается расположение 1, 2, 3, ... в возрастающем порядке): 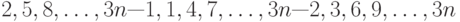 ?
?
Чему равно число инверсий в перестановке 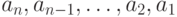 ?
?
Чему равно разложение в произведение независимых циклов подстановки  ?
?
Чему равно  , где
, где 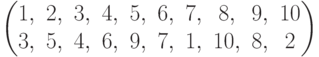 ?
?
Чему равно значение определителя: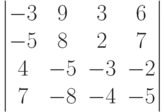 ?
?
Чему равна кратность корня 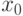 многочлена
многочлена  , где
, где 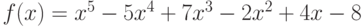 ,
, 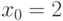 ?
?
Чему равен наибольший общий делитель многочленов 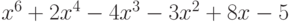 и
и 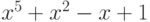 ?
?
Чему равно значение  , если
, если 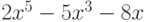 и
и 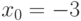 ?
?
Чему равно значение производной  в точке 2, если
в точке 2, если 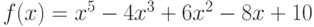 ?
?
Чему равно разложение на линейные и квадратные множители над полем вещественных чисел многочлена 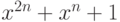 ?
?
Что представляет собой многогранник Ньютона для многочлена от одной переменной?
Чему равен минимальный редуцированный базис Грёбнера для идеала  , где
, где 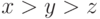 ?
?
Чему равны элементы решений следующей системы уравнений  ?
?
Чему равны элементы базиса Грёбнера при 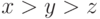 для следующей системы уравнений
для следующей системы уравнений  ?
?
Каким числом ограничена степень неприводимого множителя?
Во сколько раз отличается длина минимального вектора от длины вектора построенного с помощью алгоритма редуцированного базиса решётки,если размерность решётки равна n?
С какой точностью определено решение уравнения 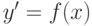 ?
?
К какому типу из перечисленных ниже относится класс функций порождаемый функцией  в любом поле из уравнения
в любом поле из уравнения 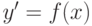 ?
?
Через какую математическую конструкцию выражаются арктангенсы при интегрировании рациональных функций с действительными коэффициентами?
В какой из приведённых алгебраических структур имеются арифметические операции наряду с операциями дифференцирования?
В каком из перечисленных случаев определен элементарный интеграл экспоненциальной функции?
В каком поле изменяется степень полинома при дифференцировании по x полинома от экспоненты со старшим коэффициентом 1?
Чему равны элементы базиса Грёбнера при 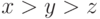 для следующей системы уравнений
для следующей системы уравнений  ?
?
При каких 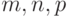 многочлен
многочлен  делится на
делится на 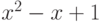 ?
?
При каких значениях  совместна система уравнений
совместна система уравнений  ?
?
Какой из приведённых алгоритмов используется в качестве алгоритма при реализации архимедовой метрики в поле комплексных чисел K заданном над полем Q?
При помощи каких из перечисленных ниже функций осуществляется интегрирование рациональных функций с действительными коэффициентами?
Какой след имеют все степени нильпонентной матрицы?
Чему равен базис линейного пространства R многочленов р(х), степень которых не выше двух и которые удовлетворяют условию р(A) = 0?
Чему равен ранг матрицы  ?
?
Чему равен ранг матрицы  ?
?
Чему равны координаты элемента 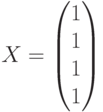 в базисе
в базисе 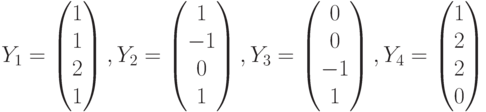 ?
?
Чему равна размерность подпространства элементов из евклидова пространства  ортогональных к данному ненулевому элементу
ортогональных к данному ненулевому элементу  ?
?
Чему равен кососимметрический определитель нечетного  -го порядка?
-го порядка?
Чему равен элемент определителя порядка  , симметричный элементу
, симметричный элементу 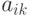 относительно побочной диагонали?
относительно побочной диагонали?
Сколько инверсий во всех перестановках  элементов вместе?
элементов вместе?
Чему равен декремент подстановки 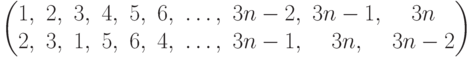 ?
?
С каким знаком приведённое ниже произведение входит в определитель соответствующего порядка: 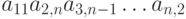 ?
?
Чему равен наибольший общий делитель многочленов: 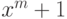 и
и 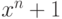 ?
?
Чему равен наибольший общий делитель многочленов  и
и 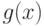 , где
, где 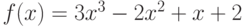 ,
, 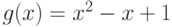 ?
?
Чему равен результат деления многочлена  на
на  , если
, если 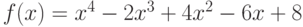 и
и  ?
?
Чему равен результат деления многочлена  на
на  , если
, если  и
и 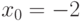 ?
?
Чему равен многочлен наименьшей степени с комплексными коэффициентами, имеющий двойной корень единица, простые корни два, три и  ?
?
Чему равен универсальный базис Грёбнера главного идеала (f), где ![f \in K[x_{1}, \ldots, x_{n}]](https://intuit.ru//sites/default/files/tex_cache/1e129f499afa38995b3eb77c2f791dab.png) ?
?
Для каких чисел реализован алгоритм построения редуцированного базиса решетки при нахождении минимального вектора решетки?
Для каких чисел норма многочлена связана с нормой комплексного числа?
В каком из перечисленных случаев определен элементарный интеграл логарифмической функции?
В каком поле определено интегрирование полиномиальной части функции методом неопределенных коэффициентов?
В каком из перечисленных полей уравнения Риша являются квадратными?
В каком кольце изменяется степень полинома при дифференцировании по x полинома от экспоненты со старшим коэффициентом 1?
Какое название носит решение 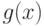 уравнения
уравнения 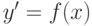 ?
?
Чему равно разложение в произведение независимых циклов подстановки 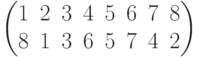 ?
?
Чему равно значение определителя:  ?
?
Чему равна размерность пространства 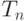 столбцов с n элементами?
столбцов с n элементами?
Каким будет результат выражение , где ? в компьютерной алгебре?
Чему равны координаты вектора х в базисе  , где
, где 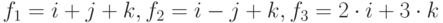 ,
, 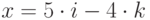 ?
?
Чему равна матрица оператора 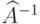 , где
, где 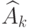 - оператор поворота на угол
- оператор поворота на угол 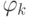 в пространстве
в пространстве 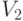 векторов на плоскости?
векторов на плоскости?
Чему равен многочлен степени четыре со старшим коэффициентом один имеющий двойной корень три и простые корни 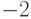 и
и 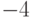 ?
?
Чему равно разложение на неприводимые множители многочлена при помощи выделения его кратных неприводимых множителей  ?
?
Конечно ли число наборов, меньших данного набора 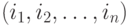 ?
?
Чему равны элементы решений следующей системы уравнений  ?
?
В каком поле рациональная функция представима в виде суммы полинома и правильной дроби?
Какие из приведённых операций имеются наряду с арифметическими операциями в кольце?
При каких значениях  совместна система уравнений
совместна система уравнений  ?
?
Чему равна размерность линейного пространства матриц  с размерами
с размерами  , элементы которых удовлетворяют условиям
, элементы которых удовлетворяют условиям  ?
?
Чему равен ранг матрицы 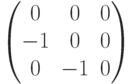 ?
?
Чему равно число рёбер многогранника Ньютона многочлена  ?
?
Для какого поля реализацован алгоритм факторизации при использовании p-адической метрики?
Какое выражение получается в результате интегрирования правильных дробей знаменатели которых являются неприводимыми полиномами?
На каким полем регулярный моном является трансцендентеным элементом, логарифмом и экспонентой одновременно?
Какая из приведённых ниже алгоритмов используется в качестве алгоритма при реализации архимедовой метрики на поле Q в комплексном случае?
Чему равен порядок элемента , если порядок элемента x равен n в компьютерной алгебре?
Чему равна размерность линейного пространства матриц  , для которых выполняется равенство
, для которых выполняется равенство  , где
, где 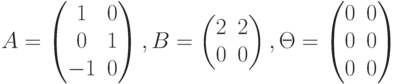 ?
?
С каким знаком приведённое ниже произведение входит в определитель соответствующего порядка: 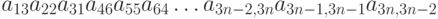 ?
?
Для каких чисел определена независимая переменная над вычислимым полем констант?
Чему равно  для пространства
для пространства  , которое изоморфно пространству
, которое изоморфно пространству 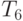 ?
?
Сколько инверсий образует число 1, стоящее на  -м месте перестановки?
-м месте перестановки?
Чему равно разложение в произведение независимых циклов подстановки 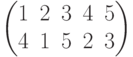 ?
?
Чему равен наибольший общий делитель многочленов  и
и 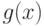 , где
, где  ,
, 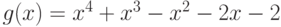 ?
?
В каком поле ядро естественного гомоморфизма кольца Z[x] совпадает с его главным идеалом?
Какая из приведённых ниже математических конструкций трансцендентна над полем, которому принадлежит её правая часть?
При каких  и
и  многочлен
многочлен  имеет двойной корень, отличный от нуля?
имеет двойной корень, отличный от нуля?
Чему равен X для системы линейных уравнений 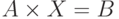 , где
, где  ?
?
Чему равен многочлен степени четыре со старшим коэффициентом один имеющий корни  ?
?

 и входящие в определитель со знаком плюс?
и входящие в определитель со знаком плюс? ) в пространстве
) в пространстве  многочленов степени, не превосходящей 2, в базисе
многочленов степени, не превосходящей 2, в базисе 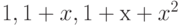 ?
?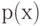 степени не выше
степени не выше  , которые удовлетворяют условию
, которые удовлетворяют условию 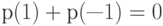 ?
? в базисе
в базисе 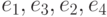 , если матрица данного линейного оператора
, если матрица данного линейного оператора  в базисе
в базисе 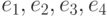 имеет вид:
имеет вид:  ?
?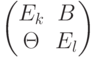 в компьютерной алгебре при условии, что Еk и El — единичные матрицы k-го и l-го порядков, В — произвольная k х l матрица?
в компьютерной алгебре при условии, что Еk и El — единичные матрицы k-го и l-го порядков, В — произвольная k х l матрица? ?
? элементами
элементами 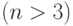 , у которых сумма первых трех элементов равна нулю?
, у которых сумма первых трех элементов равна нулю?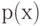 степени не выше 4, которые удовлетворяют условию
степени не выше 4, которые удовлетворяют условию 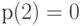 ?
?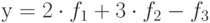 в базисе
в базисе 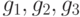 , базисы заданы своими координатами в линейном пространстве
, базисы заданы своими координатами в линейном пространстве 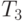 :
:
 ?
? для пространства симметричных
для пространства симметричных  - матриц с нулевыми диагональными элементами, которое изоморфно пространству
- матриц с нулевыми диагональными элементами, которое изоморфно пространству 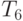 ?
? для подпространства столбцов из
для подпространства столбцов из 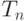 , сумма элементов которых равна нулю, которое изоморфно пространству
, сумма элементов которых равна нулю, которое изоморфно пространству 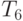 ?
? каждый из которых ортогонален к данным элементам
каждый из которых ортогонален к данным элементам 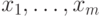
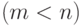 ?
? ?
? к базису
к базису 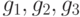 , базисы заданы своими координатами в линейном пространстве
, базисы заданы своими координатами в линейном пространстве 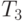 :
:
 ?
?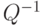 от ортонормированного базиса
от ортонормированного базиса 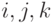 в пространстве
в пространстве 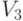 геометрических векторов к базису
геометрических векторов к базису 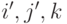 , где векторы
, где векторы  получаются соответственно из векторов
получаются соответственно из векторов  и
и  поворотом их на угол
поворотом их на угол  в плоскости этих векторов?
в плоскости этих векторов? ) в пространстве
) в пространстве  многочленов степени, не превосходящей 2, в базисе
многочленов степени, не превосходящей 2, в базисе  ?
? в базисе
в базисе 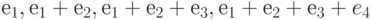 , если матрица данного линейного оператора
, если матрица данного линейного оператора  в базисе
в базисе 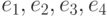 имеет вид:
имеет вид:  ?
? -го порядка, если его строки записать в обратном порядке?
-го порядка, если его строки записать в обратном порядке? , в каждом из которых в каждой строке и каждом столбце один элемент равен единице, а остальные равны нулю?
, в каждом из которых в каждой строке и каждом столбце один элемент равен единице, а остальные равны нулю?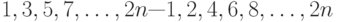 ?
?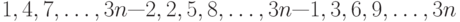 ?
?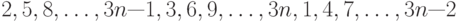 ?
?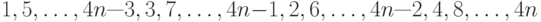 ?
? четность числа инверсий и числа порядков во всех перестановках чисел
четность числа инверсий и числа порядков во всех перестановках чисел  противоположна?
противоположна? и
и  такие, что произведение
такие, что произведение 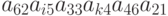 входили бы в определитель 6-го порядка со знаком минус?
входили бы в определитель 6-го порядка со знаком минус? , простой корень
, простой корень 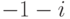 ?
?
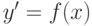 является полем рациональных функций от одной переменной?
является полем рациональных функций от одной переменной? в любом поле, если данная функция входит в уравнение вида
в любом поле, если данная функция входит в уравнение вида 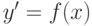 ?
? ?
? , простой корень
, простой корень 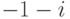
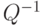 от ортонормированного базиса
от ортонормированного базиса 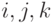 в пространстве
в пространстве 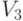 геометрических векторов к базису
геометрических векторов к базису 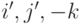 , где векторы
, где векторы  получаются соответственно из векторов
получаются соответственно из векторов  и
и  поворотом их на угол
поворотом их на угол  в плоскости этих векторов?
в плоскости этих векторов?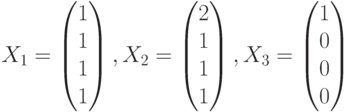 ?
? для подпространства многочленов
для подпространства многочленов 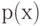 из
из 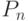 , удовлетворяющих условию
, удовлетворяющих условию 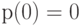 , которое изоморфно пространству
, которое изоморфно пространству 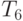 ?
? ?
?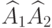 , где
, где 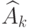 - оператор поворота на угол
- оператор поворота на угол 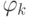 в пространстве
в пространстве 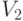 векторов на плоскости?
векторов на плоскости? в правом ортонормированном базисе
в правом ортонормированном базисе 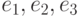 , если
, если 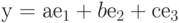 (а, b, с — заданные числа); у — фиксированный вектор линейного пространства
(а, b, с — заданные числа); у — фиксированный вектор линейного пространства 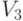 ,
,  — оператор, действие которого на любой вектор
— оператор, действие которого на любой вектор  из
из 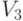 задается равенством
задается равенством ![\widehat А х = [х , у], где [х , у]](https://intuit.ru//sites/default/files/tex_cache/bb53811acdf9d1592baa14383e89273e.png) — векторное произведение вектора
— векторное произведение вектора  на вектор
на вектор  ?
? -го порядка, если первый столбец переставить на последнее место, а остальные столбцы передвинуть влево, сохраняя их расположение
-го порядка, если первый столбец переставить на последнее место, а остальные столбцы передвинуть влево, сохраняя их расположение , если из каждой строки, кроме последней, вычесть последующую строку, из последней строки вычесть прежнюю первую строку?
, если из каждой строки, кроме последней, вычесть последующую строку, из последней строки вычесть прежнюю первую строку? ?
? и
и  такие, что произведение
такие, что произведение 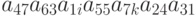 входили бы в определитель 7-го порядка со знаком плюс?
входили бы в определитель 7-го порядка со знаком плюс? ?
?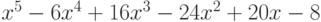 ?
? уравнения
уравнения 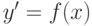 является кольцом полиномов?
является кольцом полиномов? 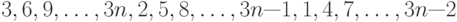 ?
?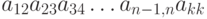 , где
, где 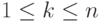 ?
?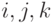 в пространстве
в пространстве 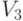 геометрических векторов к базису
геометрических векторов к базису 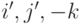 , где векторы
, где векторы  получаются соответственно из векторов
получаются соответственно из векторов  и
и  поворотом их на угол
поворотом их на угол  в плоскости этих векторов?
в плоскости этих векторов? ?
? и
и  в каждом из базисов, базисы заданы своими координатами в линейном пространстве
в каждом из базисов, базисы заданы своими координатами в линейном пространстве 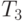 :
:
 ?
? , в каждом из которых в каждой строке и каждом столбце один элемент равен единице, а остальные равны нулю?
, в каждом из которых в каждой строке и каждом столбце один элемент равен единице, а остальные равны нулю?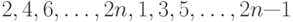 ?
? ?
?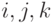 в пространстве
в пространстве 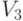 геометрических векторов к базису
геометрических векторов к базису 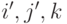 , где векторы
, где векторы  получаются соответственно из векторов
получаются соответственно из векторов  и
и  поворотом их на угол
поворотом их на угол  в плоскости этих векторов?
в плоскости этих векторов? , у которого сумма строк с четными номерами равна сумме строк с нечетными номерами?
, у которого сумма строк с четными номерами равна сумме строк с нечетными номерами? ?
? к базису
к базису 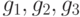 , базисы заданы своими координатами в линейном пространстве
, базисы заданы своими координатами в линейном пространстве 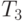 :
:
 ?
? , в базисе
, в базисе  , где
, где  - линейная оболочка функций
- линейная оболочка функций  ?
? -го порядка, если каждый его элемент заменить элементом, симметричным с данным относительно "центра" определителя?
-го порядка, если каждый его элемент заменить элементом, симметричным с данным относительно "центра" определителя?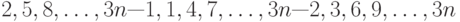 ?
? в любом поле из уравнения
в любом поле из уравнения 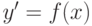 ?
? ортогональных к данному ненулевому элементу
ортогональных к данному ненулевому элементу  ?
? ?
?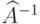 , где
, где 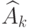 - оператор поворота на угол
- оператор поворота на угол 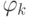 в пространстве
в пространстве 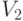 векторов на плоскости?
векторов на плоскости?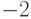 и
и 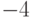 ?
? ?
? с размерами
с размерами  , элементы которых удовлетворяют условиям
, элементы которых удовлетворяют условиям  ?
?