Допустимый вектор x0 оптимальный тогда и только тогда, когда в двойственной задаче имеется такое допустимое решение y0, что:
(Отметьте один правильный вариант ответа.)
Варианты ответа
cTx0=bTy0(Верный ответ)
cTx0>bTy0
cTx0=-bTy0

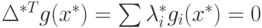 . Тогда вектор
. Тогда вектор