Функция f(x) является выпуклой на выпуклой области X, если для всех x1, x2 ∈ X выполняется соотношение:
Если для всех x1, x2 ∈ X выполняется соотношение f[θx2+(1–θ)x1]≤θf(x2)+(1–θ)f(x1) при 0 < θ < 1, то функция f(x) на выпуклой области X является:
Пусть для некоторой выпуклой вверх(вогнутой) функции f, определенной на множестве R справедливо условие: для любых x1, x2 є R и 0 ≤ k ≤ 1 f[kx1+(1–k)x2] ≤ kf(x1)+(1–k)f(x2). Тогда множество R является:
Пусть R – выпуклое множество точек n – мерного пространства. Функция f, определенная на R, называется выпуклой верх, если для любой пары точек x1, x2 є R и произвольного 0 ≤ k ≤ 1 справедливо:
Дана функция F(x). Пусть x' доставляет минимум функции F(x) на интервале [a; b] с заданной точностью ξ. Известно, что F1 и F2 – значения функции F(x) в окрестности ±ξ вычисленной точки x=(a+b)/2. При поиске минимума был отброшен отрезок [x; b], т.е. b = x. Это значит, что:
Дана функция F(x). Известно, что x' доставляет некоторый экстремум функции F(x) на интервале [a; b] с заданной точностью ξ. При этом F1 и F2 – значения функции F(x) в окрестности ±ξ вычисленной точки x=(a+b)/2. Если F1 < F2, т.е. b = x, то:
Дана функция F(x). Пусть x' доставляет минимум функции F(x) на интервале [a; b] с заданной точностью ξ. Известно, что F1 и F2 - значения функции F(x) в окрестности ±ξ вычисленной точки x=(a+b)/2. Если F1 < F2, то:
Пусть некоторое открытое множество Rn содержит точку x*. Известно, что x* является точкой минимума функции f(x) при ограничениях gi(x) ≤ 0, i=1,...,m, удовлетворяющих условию регулярности в виде линейной независимости векторов Δgi(x*), и существуют такие неотрицательные множители Лагранжа λ1,...,λm, что Δf(x*) + ΣλiΔgi(x*) = 0;Σλigi(x*) = 0, λi ≥ 0, i = 1,...,m. Тогда функции gi(x), i = 1,...,m:
Пусть
f(x1,...,xn) дифференцируема в некоторой допустимой области
R. Если для данной функции выполняется условие
∂f(x0)/∂xj = 0, j=1,...,n, то в некоторой внутренней точке
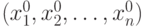
области
R функция:
Пусть функции gi(x), i=1,...,m имеют непрерывные частные производные на некотором открытом множестве Rn, содержащем точку x*. Если для функции f(x) ограничения gi(x) ≤ 0, i=1,...,m удовлетворяют условию регулярности в виде линейной независимости векторов Δgi(x*), и существуют такие неотрицательные множители Лагранжа λ1,...,λm, что Δf(x*) + ΣλiΔgi(x*) = 0;Σλigi(x*) = 0, λi ≥ 0, i = 1,...,m является:

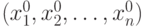 области
области