Пусть f(x) и все gi(x) выпуклы и все функции gi(x) удовлетворяют условию регулярности Слейтера. Вектор x* решением задачи нелинейного программирования: минимизировать f(x) при условиях gi(x) ≤ 0, i = 1,...,m тогда и только тогда, когда существует такой вектор Δ* ≥ 0, для которого выполняются условия:
Дана функция F(x). Известно, что x' доставляет некоторый экстремум функции F(x) на интервале [a; b] с заданной точностью ξ. При этом F1 и F2 – значения функции F(x) в окрестности ±ξ вычисленной точки x=(a+b)/2. Если F1 < F2, т.е. b = x, то:
Дана функция F(x). Пусть x' доставляет минимум функции F(x) на интервале [a; b] с заданной точностью ξ. Известно, что F1 и F2 – значения функции F(x) в окрестности ±ξ вычисленной точки x=(a+b)/2. При поиске минимума был отброшен отрезок [x; b], т.е. b = x. Это значит, что:
Дана функция F(x). Пусть x' доставляет минимум функции F(x) на интервале [a; b] с заданной точностью ξ. Известно, что F1 и F2 - значения функции F(x) в окрестности ±ξ вычисленной точки x=(a+b)/2. Если F1 < F2, то:
Пусть
f(x) и все
gi(x) выпуклы и все функции
gi(x) удовлетворяют условию регулярности Слейтера. Задача нелинейного программирования задана следующим образом: минимизировать
f(x) при условиях
gi(x) ≤ 0, i = 1,...,m. Пусть существует некоторый вектор
Δ* ≥ 0, такой, что
L(x*,Δ) ≤ L(x*,Δ*) ≤ L(x,Δ*) и
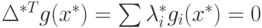
. Тогда вектор
Δ*:
Предположим, что имеется интервал неопределенности (x1; x3) и известно значение f(x2) внутри этого интервала. Положим x2–x1 = L и x3–x2 = R. Если x4 находится в интервале (x1; x2) и новым интервалом неопределенности будет (x1; x2) длиной x2–x1 = L, то в этом случае:
Пусть некоторое открытое множество Rn содержит точку x*. Известно, что x* является точкой минимума функции f(x) при ограничениях gi(x) ≤ 0, i=1,...,m, удовлетворяющих условию регулярности в виде линейной независимости векторов Δgi(x*), и существуют такие неотрицательные множители Лагранжа λ1,...,λm, что Δf(x*) + ΣλiΔgi(x*) = 0;Σλigi(x*) = 0, λi ≥ 0, i = 1,...,m. Тогда функции gi(x), i = 1,...,m:
Пусть n – мерный вектор x является псевдопланом, для которого выполняются условия: Δj ≥ 0, j=1,...,n;. Тогда справедливы равенства:
Пусть функции gi(x), i=1,...,m имеют непрерывные частные производные на некотором открытом множестве Rn, содержащем точку x*. Если для функции f(x) ограничения gi(x) ≤ 0, i=1,...,m удовлетворяют условию регулярности в виде линейной независимости векторов Δgi(x*), и существуют такие неотрицательные множители Лагранжа λ1,...,λm, что Δf(x*) + ΣλiΔgi(x*) = 0;Σλigi(x*) = 0, λi ≥ 0, i = 1,...,m является:
Пусть функции gi(x), i=1,...,m имеют непрерывные частные производные на некотором открытом множестве Rn, содержащем точку x*. Если x* является точкой минимума функции f(x) при ограничениях gi(x) ≤ 0, i=1,...,m, удовлетворяющих условию регулярности в виде линейной независимости векторов Δgi(x*), то существуют такие неотрицательные множители Лагранжа λ1,...,λm, что справедливы соотношения:

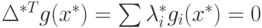 . Тогда вектор
. Тогда вектор