Укажите распределение разности двух независимых случайных величин с одним и тем же нормальным распределением с параметрами  .
.
(Отметьте один правильный вариант ответа.)
Варианты ответа
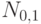
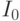
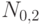
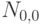

 .
.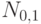
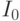
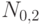
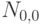
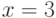 плотности распределения суммы трех независимых в совокупности случайных величин с одним и тем же нормальным распределением с параметрами
плотности распределения суммы трех независимых в совокупности случайных величин с одним и тем же нормальным распределением с параметрами  .
.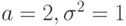 . Пусть
. Пусть  - сумма первых
- сумма первых  случайных величин в этой последовательности. Последовательность
случайных величин в этой последовательности. Последовательность  слабо сходится к некоторому распределению. Найдите это распределение.
слабо сходится к некоторому распределению. Найдите это распределение.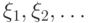 — последовательность независимых случайных величин с одним и тем же нормальным распределением с параметрами
— последовательность независимых случайных величин с одним и тем же нормальным распределением с параметрами 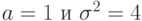 . Укажите, чему равен предел при
. Укажите, чему равен предел при 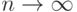 последовательности
последовательности 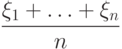
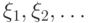 — последовательность независимых случайных величин с одним и тем же нормальным распределением с параметрами
— последовательность независимых случайных величин с одним и тем же нормальным распределением с параметрами 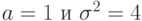 . Укажите, чему равен предел при
. Укажите, чему равен предел при 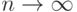 последовательности
последовательности 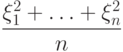
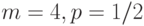 . Пусть
. Пусть  - сумма первых
- сумма первых  случайных величин в этой последовательности. Последовательность
случайных величин в этой последовательности. Последовательность  слабо сходится к некоторому распределению. Найдите это распределение.
слабо сходится к некоторому распределению. Найдите это распределение.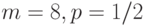 . Пусть
. Пусть  - сумма первых
- сумма первых  случайных величин в этой последовательности. Последовательность
случайных величин в этой последовательности. Последовательность 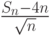 слабо сходится к некоторому распределению. Найдите это распределение.
слабо сходится к некоторому распределению. Найдите это распределение.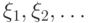 — последовательность независимых случайных величин с одним и тем же биномиальным распределением с параметрами
— последовательность независимых случайных величин с одним и тем же биномиальным распределением с параметрами 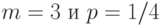 . Укажите, чему равен предел при
. Укажите, чему равен предел при 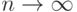 последовательности
последовательности 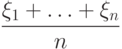
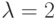 ,
,  - сумма первых
- сумма первых  случайных величин в этой последовательности. Последовательность
случайных величин в этой последовательности. Последовательность  слабо сходится к некоторому распределению. Найдите это распределение.
слабо сходится к некоторому распределению. Найдите это распределение.![[-1, 1]](https://intuit.ru//sites/default/files/tex_cache/7dec1d46e68831c4eca28b020fcb1604.png) ,
,  - сумма первых
- сумма первых  случайных величин в этой последовательности. Последовательность
случайных величин в этой последовательности. Последовательность  слабо сходится к некоторому распределению. Найдите это распределение.
слабо сходится к некоторому распределению. Найдите это распределение.