Какие из операций коммутативны?
Какие из перечисленных систем функций функционально полны в слабом смысле?
Множества A, B, C выражены через три других множества D, E, F следующими равенствами (знак пересечения опущен): A = D∪EF, B = ((D\E)∪E)F, С = DF∪EF. Отметьте верное равенство:
Сколько различных слов можно получить перестановками букв в слове abcd?
Функция f(x1,x2) имеет тип AB→C, функция g(y1,y2) имеет тип AC→A. Какой тип имеет функция f(g(y1,y2),x2)?
Сколькими способами можно выбрать гласную и согласную буквы из слова «схема»?
На множестве действительных чисел задано отношение |x-y|<5. Отметьте верное утверждение:
Отметьте графы, в которых возможна топологическая сортировка:
Чему равен единичный элемент в группе целых степеней двойки с умножением?
Даны два множества: A = {a,b,c}, B = {0,1}. Каково число различных функций типа AB2→B2?
Какие из множеств замкнуты относительно сложения?
Какое расстояние между двумя вершинами возможно графе с 4 вершинами?
Сколько существует двухэлементных подмножеств множества {a,b,c,d}?
Чему равна проекция множества A = {(1,4),(2,1),(2,3),(4,3)} на первую координату?
Чему равно число таблиц размером 3x2 с элементами из множества мощности 3?
Какие из множеств с указанной операцией над элементами образуют полугруппу?
Чему равна наибольшая нижняя грань для {c,f}? 
Каково число логических функций от 4 переменных?
Какие из операций над множествами ассоциативны?
Каким может быть дополнение к отношению эквивалентности?
Соответствие G между множествами A = {a,b,c,d} и B = {1,2,3,4} задано множеством пар G = {(a,2),(b,1),(c,1),(d,4)}. Отметьте верные утверждения:
Чему равна наименьшая верхняя грань для {c,g}? 
Отметьте каким является граф заданный матрицей смежности:
| 0 | 1 | 1 | 1 | 0 |
| 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 |
Какие из операций ассоциативны?
Встретились 6 друзей, и каждый пожал руку каждому. Сколько всего было рукопожатий?
На вершину горы ведут пять дорог. Сколькими способами турист может подняться на гору и спуститься с нее?
Какой элемент является образующей в группе {-1,1} с умножением?
Функция f задана таблицей:
| x | y | z | f |
|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
Какой из полиномов Жегалкина ей соответствует?
Сколько ребер могут иметь простые графы без петель с 6 вершинами?
Какая из формул эквивалентна формуле (x&¬y)∨(y&z)∨(¬y&z)?
Даны множества A = {a,b,d,e,f}, B = {b,c,e,g}, С = {a,d,f}. Отметьте верное равенство:
Множество A содержит 6 элементов, множество B содержит 7 элементов. Сколько элементов может содержать их объединение?
Множества A, B, C выражены через три других множества D, E, F следующими равенствами (знак пересечения опущен): A = D\(E∪F), B = DE∪DF, C = (D\E)∩(D\F). Отметьте верное равенство:
Чему равна проекция множества A = {(1,3),(2,3),(2,4),(3,1)} на вторую координату?
Соответствие G между множествами A = {a,b,c,d,e} и B = {1,2,3,4} задано множеством пар G = {(a,2),(a,3),(b,3),(c,1),(e,3),(e,4)}. Какое из множеств является прообразом элемента 3 при этом соответствии?
Соответствие G между множествами A = {a,b,c,d} и B = {1,2,3,4} задано множеством пар G = {(a,1),(b,2),(b,3),(c,1),(d,3)}. Отметьте верное утверждение:
Какое из множеств является конечным?
Между множествами A = {a,b,c,d} и B = {1,2,3,4} множеством пар заданы соответствия G = {(a,1),(c,3),(d,3),(d,4)} и H = {(a,2),(b,1),(c,3),(d,3)}. Какое соответствие функционально?
Функция f(x1,x2) имеет тип AC→B, функция g(y1,y2) имеет тип AC→C. Какой тип имеет функция f(x1,g(y1,y2))?
Объединение двух отношений частичного порядка будет отношением частичного порядка ...
На множестве A = {a,b,c,d} задано бинарное отношение R = {(a,d),(b,d),(d,c)}. Какие пары нужно добавить к R, чтобы получить его транзитивное замыкание?
Сколько четных двузначных чисел можно составить из цифр 2,3,6,7,9 (каждую цифру в числе можно использовать только 1 раз)?
В группе из 20 человек 5 человек сдали экзамен по истории на «отлично», 7 человек сдали экзамен по высшей математике на «отлично» и 2 человека сдали экзамен по обоим предметам на «отлично». Сколько человек в группе не сдали на «отлично» ни экзамен по истории, ни экзамен по высшей математике?
Надо послать 4 срочных письма. Сколькими способами можно это сделать, если для передачи писем можно послать трех курьеров и каждое письмо можно дать любому из курьеров?
В группе из 20 человек нужно выбрать старосту и профорга. Сколькими способами это можно сделать?
Сколько различных слов можно получить перестановками букв в слове abc?
Сколькими способами из 10 спортсменов можно отобрать команду из 6 человек?
В кондитерском магазине продавались три сорта пироженных: эклеры, наполеоны и слоеные. Сколькими способами можно купить 4 пироженных?
Какими из следующих свойств обладают биномиальные коэффициенты?
Слова длины 5 в алфавите {a,b,c,d} перечисляются в лексикографическом порядке. Слово ааааа имеет номер 0. Какой номер будет иметь слово abcad?
Чему равно число таблиц размером 23 с элементами из множества мощности 3?
Какие из операций ассоциативны?
Отметьте дистрибутивны слева множества:
Отметьте подмножества, которые в алгебре действительных чисел с умножением образуют подалгебру:
Какие из множеств с указанной операцией над элементами образуют полугруппу?
Какие из множеств с операцией сложения образуют группу?
Какие из множеств с указанной операцией над элементами образуют группу?
Чему равен единичный элемент в группе целых чисел со сложением?
Чему равна наименьшая верхняя грань для {b,f}? 
Чему равна наибольшая нижняя грань для {e,g}? 
Каково число логических функций от 5 переменных?
В таблице приведены три функции f1, f2, f3 от переменных x, y, z:
| x | y | z | f1 | f2 | f3 |
|---|
| 0 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 | 0 |
Какие из этих функций содержат несущественные переменные?
Какие из функций ассоциативны?
Функция f задана таблицей:
| x | y | z | f |
|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
Какой из полиномов Жегалкина ей соответствует?
Какие из функций являются монотонными?
Какие из функций являются линейными?
Какие из перечисленных систем функций функционально полны в слабом смысле?
В таблице приведены три функции f1, f2, f3 от переменных x, y, z:
| x | y | z | f1 | f2 | f3 |
|---|
| 0 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 0 | 0 | 0 |
| 1 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 | 0 | 1 |
| 1 | 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 |
Какие из этих функций функционально полны в слабом смысле?
Дано равенство ∀x∃yP(x,y) = ∃x∀yP(x,y). Какие из утверждений верны?
Какая из формул исчисления предикатов выражает тот факт, что в множестве М, в котором определен частичный порядок, не существует минимального элемента?
Отметьте неверную формулу:
Существуют ли простые графы без петель с 4 вершинами со следующим набором степеней:
Какой радиус может быть у графа с 6 вершинами?
Какое расстояние между двумя вершинами возможно графе с 6 вершинами?
Какие из графов, приведенных на рисунке, являются эйлеровыми? 
Граф задан матрицей смежности:
| 0 | 1 | 1 | 0 | 1 |
| 0 | 0 | 0 | 1 | 1 |
| 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 |
Отметьте каким он является:
Какие графы могут совпадать со своим графом конденсации?
Дан ациклический граф с n вершинами. Сколько в нем может быть вершин, которые не являются ни источниками, ни стоками?
Сколько висячих вершин может быть у дерева с n вершинами?
В потоковой сети, приведенной на рисунке, все пропускные способности равны 4:  Нарушены ли в ней правила распределения потоков?
Нарушены ли в ней правила распределения потоков?
Для любого k число путей длины k, начинающихся с любой вершины графа G, всегда одинаково, если
Степень Cn матрицы смежности C ориентированного графа G содержит ненулевые элементы во всех клетках главной диагонали если:
Какие из операций ассоциативны?
Сколькими способами можно выбрать гласную и согласную буквы из слова «пехота»?
Сколько различных слов можно получить перестановками букв в слове abcde?
Между множествами A = {a,b,c,d} и B = {1,2,3,4} множеством пар заданы соответствия G = {(a,1),(b,1),(c,3),(d,4)} и H = {(a,1),(c,1),(c,3),(d,4)}. Какое соответствие функционально?
Слова длины 5 в алфавите {a,b,c,d} перечисляются в лексикографическом порядке. Слово ааааа имеет номер 0. Какой номер будет иметь слово bcacd?
В некоторых видов спортивных соревнований исходом является определение участников, занявших первое, второе и третье места. В соревновании участвует 10 человек. Сколько возможно различных исходов?
В группе из 15 человек 6 человек увлекаются театром, 8 человек увлекаются спортом и 3 человека увлекаются и театром, и спортом. Сколько человек в группе не увлекаются ни театром, ни спортом?
Какие из операций коммутативны?
Какие из множеств с указанной операцией над элементами образуют группу?
Даны множества 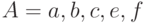 ,
, 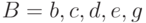 ,
, 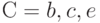 . Отметьте верное равенство:
. Отметьте верное равенство:
Отметьте неверную формулу:
Множество A содержит 5 элементов, множество B содержит 8 элементов. Сколько элементов может содержать их пересечение?
Между множествами A = {a,b,c,d} и B = {1,2,3,4} множеством пар заданы соответствия G = {(b,1),(c,2),(d,2),(d,3)} и H = {(a,2),(b,2),(c,4),(d,1)}. Какое соответствие функционально?
Какие из множеств с операцией сложения образуют группу?
В таблице приведены три функции f1, f2, f3 от переменных x, y, z:
| x | y | z | f1 | f2 | f3 |
|---|
| 0 | 0 | 0 | 1 | 1 | 1 |
| 0 | 0 | 1 | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 0 | 1 | 0 |
| 1 | 0 | 1 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 0 | 1 |
Какие из этих функций содержат несущественные переменные?
Какая из формул исчисления предикатов выражает тот факт, что в множестве М, в котором определен частичный порядок, существует максимальный элемент?
В потоковой сети, приведенной на рисунке, все пропускные способности равны 4:  Нарушены ли в ней правила распределения потоков?
Нарушены ли в ней правила распределения потоков?
Какие из множеств с указанной операцией над элементами образуют группу?
Граф является двудольным, если он ...
Какие из перечисленных систем функций функционально полны в слабом смысле?
Между точками горизонтальной прямой задано отношение «левее» (x левее y). Отметьте верное утверждение:
Каково число логических функций от 3 переменных?
Дано равенство ∀x∀yP(x,y) = ∃x∃yP(x,y). Какие из утверждений верны?
Каким может быть ориентированное дерево?
Сколько ребер могут иметь простые графы без петель с 5 вершинами?
Отметьте подмножества, которые в алгебре целых чисел с умножением образуют подалгебру:
Соответствие G между множествами A = {a,b,c,d,e} и B = {1,2,3,4} задано множеством пар G = {(a,2),(b,1),(c,3),(d,1),(d,4),(e,3)}. Какое из множеств является образом элемента d при этом соответствии?
На множестве A = {a,b,c,d} задано бинарное отношение R = {(a,b),(b,c),(b,d)}. Какие пары нужно добавить к R, чтобы получить его транзитивное замыкание?
Сколькими способами можно выбрать гласную и согласную буквы из слова «здание»?
В группе из 17 человек английский язык изучают 10 человек, французский язык изучают 6 человек и оба языка изучают 2 человека. Сколько человек в группе не изучает ни английский, ни французский языки?
Сколькими способами можно выбрать три различные краски из имеющихся пяти (порядок красоок важен)?
В почтовом отделении имеются открытки 3 видов. Сколькими способами можно купить набор из 5 открыток?
Какими из следующих свойств обладают биномиальные коэффициенты?
Даны три множества: A = {a,b,c}, B = {-1,1}, C = {0,1}. Каково число различных функций типа AB*C2?
Какие из множеств замкнуты относительно сложения?
Какие из операций коммутативны?
Какие из множеств с операцией сложения образуют группу?
Чему равен единичный элемент в группе {-1,1} с умножением?
Какие из функций ассоциативны?
В таблице приведены три функции f1, f2, f3 от переменных x, y, z:
| x | y | z | f1 | f2 | f3 |
|---|
| 0 | 0 | 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 0 | 1 | 0 |
| 0 | 1 | 0 | 0 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 | 1 |
| 1 | 0 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 0 | 1 |
| 1 | 1 | 0 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 | 1 | 1 |
Какие из этих функций функционально полны в слабом смысле?
Какая из формул исчисления предикатов выражает тот факт, что в множестве М, в котором определен частичный порядок, не существует максимального элемента?
Отметьте неверную формулу:
Существуют ли простые графы без петель с 5 вершинами со следующим набором степеней:
Какие из графов, приведенных на рисунке, являются эйлеровыми? 
Во сколько цветов можно раскрасить цикл, содержащий 9 вершин?
Какие из множеств замкнуты относительно умножения?
Сколько центров может быть у дерева с n вершинами?
Какая из формул эквивалентна формуле (¬x&y)∨(x&z)∨(¬x&z)?
Какие из функций являются монотонными?
В таблице приведены три функции f1, f2, f3 от переменных x, y, z:
| x | y | z | f1 | f2 | f3 |
|---|
| 0 | 0 | 0 | 0 | 1 | 0 |
| 0 | 0 | 1 | 0 | 0 | 0 |
| 0 | 1 | 0 | 0 | 0 | 0 |
| 0 | 1 | 1 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 | 1 |
| 1 | 0 | 1 | 1 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 | 1 | 1 |
Какие из этих функций функционально полны в слабом смысле?
Какой радиус может быть у графа с 4 вершинами?
В таблице приведены три функции f1, f2, f3 от переменных x, y, z:
| x | y | z | f1 | f2 | f3 |
|---|
| 0 | 0 | 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 | 1 | 0 |
| 0 | 1 | 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 | 1 |
| 1 | 0 | 1 | 1 | 0 | 0 |
| 1 | 1 | 0 | 1 | 1 | 0 |
| 1 | 1 | 1 | 0 | 0 | 1 |
Какие из этих функций содержат несущественные переменные?
Чему равна наибольшая нижняя грань для {b,d}? 
Какие из операций над множествами коммутативны?
Какие из множеств являются счетными?
Функция f задана таблицей:
| x | y | z | f |
|---|
| 0 | 0 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 1 | 1 | 1 |
Какой из полиномов Жегалкина ей соответствует?
Даны множества A = {a,b,d,e}, B = {b,c,e,f,g}, С = {c,f,g}. Отметьте верное равенство:
Соответствие G между множествами A = {a,b,c,d,e} и B = {1,2,3,4} задано множеством пар G = {(a,1),(b,2),(b,3),(c,1),(c,4),(e,3)}. Какое из множеств является образом элемента b при этом соответствии?
На множестве A = {a,b,c,d} задано бинарное отношение R = {(a,b),(a,c),(b,c),(c,d)}. Какие пары нужно добавить к R, чтобы получить его транзитивное замыкание?
Какими из следующих свойств обладают биномиальные коэффициенты?
Какой элемент является образующей в группе целых степеней двойки с умножением?
Какая из формул эквивалентна формуле (x&y)∨(y&z)∨(¬y&z)?
Какая из функций является линейной?
Какой радиус может быть у графа с 5 вершинами?
Какое расстояние между двумя вершинами возможно графе с 5 вершинами?
Какие из графов, приведенных на рисунке, являются эйлеровыми? 
Отметьте возможные длины максимального пути в ациклическом графе с 6 вершинами и 5 ребрами:
В потоковой сети, приведенной на рисунке, все пропускные способности равны 4:  Нарушены ли в ней правила распределения потоков?
Нарушены ли в ней правила распределения потоков?
Ориентированный граф G содержит циклы. Какое из утверждений всегда верно?
Сколькими способами можно составить трехцветный полосатый флаг, если имеется материал пяти различных цветов?
Какая из функций являются монотонной?
Множество A содержит 5 элементов, множество B содержит 8 элементов. Сколько элементов может содержать разность A\B?
Какую длину может иметь максимальный путь в ациклическом графе с n вершинами?
Соответствие G между множествами A = {a,b,c,d} и B = {1,2,3,4} задано множеством пар G = {(a,2),(c,1),(c,3),(d,3),(d,4)}. Отметьте верное утверждение:
Какие из функций являются линейными?
Множества  ,
,  ,
,  выражены через три других множества
выражены через три других множества 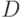 ,
,  ,
,  следующими равенствами:
следующими равенствами: 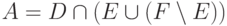 ,
, 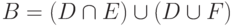 ,
,  . Отметьте верное равенство:
. Отметьте верное равенство:
Какие из множеств имеют мощность континуума:
Функция f(x1,x2) имеет тип A2*B, функция g(y1,y2) имеет тип CA*A. Какой тип имеет функция f(x1,g(y1,y2))?
Каким может быть дополнение к отношению строгого порядка?
Трое студентов сдают экзамен. Сколькими способами могут быть поставлены им отметки, если известно, что никто из них не получил неудовлетворительной отметки?
В палитре художника 5 различных красок. Художник берет кистью наугад любую из красок и ставит цветное пятно на ватмане. Затем берет следующую кисть, окунает ее в любую из красок и делает второе пятно по соседству. Сколько различных комбинаций существует для трех пятен? Порядок пятен на ватмане не важен?
Отметьте подмножества, которые в алгебре целых чисел со сложением образуют подалгебру:
Какие из множеств с указанной операцией над элементами образуют полугруппу?
Какой элемент является образующей в группе целых чисел со сложением?
Чему равна наименьшая верхняя грань для {c,e}? 
Дано равенство ∀x∃yP(x,y) = ∃y∀xP(x,y). Какие из утверждений верны?
Существуют ли простые графы без петель с 6 вершинами со следующим набором степеней:
Сколько ребер могут иметь простые графы без петель с 4 вершинами?
Чему равно число таблиц размером 33 с элементами из множества мощности 2?
Каким может быть граф конденсации?
Даны три множества: A = {1,2,3}, B = {a,b}, C = {0,1}. Каково число различных функций типа AB2→C?
Чему равна проекция множества A = {(1,2),(1,3),(2,3),(3,4)} на первую координату?
Слова длины 5 в алфавите {a,b,c,d} перечисляются в лексикографическом порядке. Слово ааааа имеет номер 0. Какой номер будет иметь слово caabd?
Сколько нечетных двузначных чисел можно составить из цифр 1,2,5,7,8 (цифры можно использовать только 1 раз)?
На множестве натуральных чисел задано отношение «x+y делится на 2». Отметьте верное утверждение:
Какие из функций ассоциативны?
 Нарушены ли в ней правила распределения потоков?
Нарушены ли в ней правила распределения потоков?  Нарушены ли в ней правила распределения потоков?
Нарушены ли в ней правила распределения потоков? 


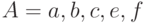 ,
, 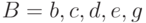 ,
, 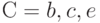 . Отметьте верное равенство:
. Отметьте верное равенство: 

 Нарушены ли в ней правила распределения потоков?
Нарушены ли в ней правила распределения потоков?  ,
,  ,
,  выражены через три других множества
выражены через три других множества 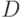 ,
,  ,
,  следующими равенствами:
следующими равенствами: 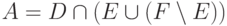 ,
, 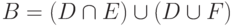 ,
,  . Отметьте верное равенство:
. Отметьте верное равенство: