Укажите условие существования системы общих представителей для разбиений 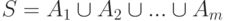 и
и 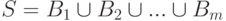 :
:
(Отметьте один правильный вариант ответа.)
Варианты ответа
каждое из множеств  и
и 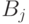 непусто
непусто
 и
и 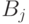 непусто
непусто
любые  множеств
множеств  содержатся не менее, чем в
содержатся не менее, чем в  множествах
множествах 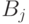 :(Верный ответ)
:(Верный ответ)
 множеств
множеств  содержатся не менее, чем в
содержатся не менее, чем в  множествах
множествах 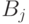 :(Верный ответ)
:(Верный ответ)
множества  попарно не пересекаются и множества
попарно не пересекаются и множества 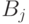 попарно не пересекаются
попарно не пересекаются
 попарно не пересекаются и множества
попарно не пересекаются и множества 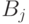 попарно не пересекаются
попарно не пересекаются

 при разбиениях множества
при разбиениях множества 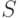
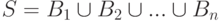 , для
, для 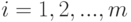 ,
, 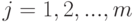 :
: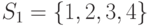 ,
, 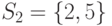 ,
, 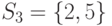 ,
, 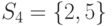 исходного множества
исходного множества 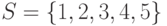
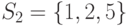 ,
, 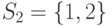 ,
,  ,
, 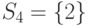 исходного множества
исходного множества 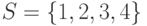
 множеств
множеств 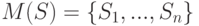 для первых
для первых  множеств,
множеств, 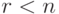 , удалось выбрать различных представителей, но все элементы множества
, удалось выбрать различных представителей, но все элементы множества 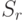 уже использованы в качестве представителей предыдущих множеств. Тогда:
уже использованы в качестве представителей предыдущих множеств. Тогда: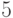 объектов на
объектов на  непустых класса равно
непустых класса равно 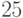 . Вычислите количество сюръективных отображений из множества, содержащего
. Вычислите количество сюръективных отображений из множества, содержащего  объектов на
объектов на 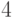 непустых класса равно
непустых класса равно  . Вычислите количество сюръективных отображений из множества, содержащего
. Вычислите количество сюръективных отображений из множества, содержащего  объектов на
объектов на  классов, таких что объект с номером
классов, таких что объект с номером 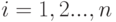 последовательно выбрали
последовательно выбрали 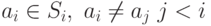 . Тогда выбранный набор
. Тогда выбранный набор 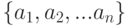 :
: