Дискретный анализ - ответы
Количество вопросов - 387
Количество слов длины  в алфавите из
в алфавите из  символов равно:
символов равно:
Что из перечисленного ниже есть система различных представителей для системы подмножеств 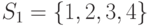 ,
, 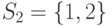 ,
,  ,
, 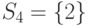 исходного множества
исходного множества 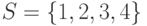
С помощью каких операций можно получить отрицание из любой немонотонной функции алгебры логики:
Укажите полную систему функций:
К каким классам функций алгебры логики относится функция 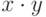 :
:
Как формально определяется множество ребер неориентированного графа:
Определите сложность решения задачи поиска кратчайших путей в графе с неотрицательными весами ребер  - количество вершин графа:
- количество вершин графа:
Что соответствует понятию сюръективного отображения в терминах слов длины  в алфавите из
в алфавите из  символов:
символов:
Какой граф называют плоским:
Для простого графа с  вершинами укажите количества ребер, обеспечивающие связность графа:
вершинами укажите количества ребер, обеспечивающие связность графа:
Многочлен Жегалкина для функции 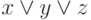 имеет вид:
имеет вид:
Укажите количество произвольных отображений из множества 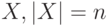 , в множество
, в множество  :
:
Сколько существует способов закупить 5 компьютеров из имеющихся 3 типов:
К классу линейных функций алгебры логики относятся:
Определите производящую функцию для последовательности 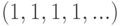 :
:
К каким классам функций алгебры логики относится функция  :
:
Чему равна сумма полиномиальных коэффициентов разложения по степеням выражения 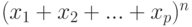 :
:
Полный простой путь длины 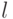 имеет тип цикла, если выполняется условие:
имеет тип цикла, если выполняется условие:
Определите взаимосвязь между формулой и функцией алгебры логики:
Класс функций заданный как 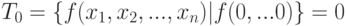 является
является
Укажите верные способы выразить нижнюю степень переменной через степени переменной:
Количество деревьев, которое можно построить на  заданный вершинах, равно:
заданный вершинах, равно:
Для двух чисел Стирлинга 1 рода, не равных нулю, 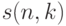 и
и  :
:
Как называется граф, в котором есть и ориентированные, и неориентированные ребра:
Укажите функции, наличие которых требуется в системе функций для получения из них операциями суперпозиции и замены переменных функций 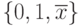 :
:
Какие из формул равносильны формуле 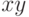 :
:
Слово длины  - это:
- это:
Какова первоначальная формулировка задачи о кенигсбергских мостах:
Максимальное количество ребер в простом графе с  вершинами и
вершинами и  компонентами связности равно:
компонентами связности равно:
Чему равно число Белла для множества из 3 элементов:
Некоторая функция алгебры логики зависит от 64 аргументов. Областью определения данной функции алгебры логики является множество с количеством элементов:
Некоторая функция алгебры логики зависит от одного аргумента. Областью определения данной функции алгебры логики является множество с количеством элементов:
Какие из функций алгебры логики принимают значение при значениях аргументов 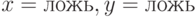
Какие из функций алгебры логики принимают значение при значениях аргументов 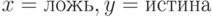
Какие из записей являтся формулами:
Какие из записей являтся формулами, если  и
и  - формулы:
- формулы:
В каких случаях имеет место указанная равносильность формул:
В каких случаях имеет место указанная равносильность формул:
Что является разложением функции алгебры логики  в дизъюнктивную форму по переменной
в дизъюнктивную форму по переменной 
Совершенная дизъюнктивная нормальная форма функции алгебры логики:
Cовершенная дизъюнктивная нормальная форма для импликации  имеет вид:
имеет вид:
Если операциями суперпозиции и замены переменных из функций данной системы функций алгебры логики можно получить произвольную функцию алгебры логики, то такая система функций:
Сколько существует функций алгебры логики от  переменных:
переменных:
К классу функций алгебры логики, сохраняющих ноль, относятся:
Инструментами для получения новых функций из уже имеющихся являются:
Количество линейных функций алгебры логики от n переменных равно:
Какое значение принимает самодвойственная функция на наборе  , если на наборе
, если на наборе 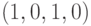 эта функция принимает значение
эта функция принимает значение  :
:
Количество самодвойственных функций алгебры логики от n переменных равно:
Для определения монотонной функции алгебры логики:
К каким классам функций алгебры логики относится функция  :
:
Любая функция алгебры логики представима единственным образом в виде:
Сколько коэффициентов в многочлене Жегалкина от трех переменных:
Укажите системы функций, не являющихся полными:
Многочлен Жегалкина для функции  имеет вид:
имеет вид:
Многочлен Жегалкина для функции  имеет вид:
имеет вид:
Укажите необходимое свойство системы функций, из которых можно получить набор функций  :
:
С помощью каких операций можно получить конъюнкцию из любой нелинейной функции алгебры логики:
Для того, чтобы система функций  была полна, необходимо и достаточно, чтобы:
была полна, необходимо и достаточно, чтобы:
Объект  может быть выбран
может быть выбран  различными способами, после этого объект
различными способами, после этого объект  может быть выбран
может быть выбран  различными способами. Тогда:
различными способами. Тогда:
Имеется 5 путевок на Байкал и 8 путевок на Родос. Сколько существует способов выбрать одну поездку?
Задача о числе функций (отображений) и задача о размещении объектов по ящикам
Упорядоченное размещение объектов по ящикам предполагает, что:
Укажите количество различных слов длины  в алфавите из
в алфавите из  символов:
символов:
Укажите количество способов разместить 4 шарика по 5 лункам:
Укажите выражения, равные количеству всевозможных размещений  различных объектов по
различных объектов по  различным ящикам при условии, что в каждом ящике не более 1 объекта:
различным ящикам при условии, что в каждом ящике не более 1 объекта:
Укажите количество способов поставить четырем студентам оценки "удовлетворительно", "хорошо", "отлично", чтобы все студенты получили разные оценки:
Укажите выражения, равные количеству взаимнооднозначных отображений из множества  на себя, где
на себя, где  - конечное множество из
- конечное множество из  элементов:
элементов:
Укажите количество различных слов длиной в 5 символов, в которых все символы различны, в алфавите из 5 символов:
Числа Стирлинга первого рода - это:
Чему равно число Стирлинга первого рода  :
:
Укажите, где способы упорядоченного размещения семи различных цифр 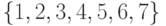 по 3 различным ящикам различны:
по 3 различным ящикам различны:
Выражение  еще называют так:
еще называют так:
Сколько существует способов закупить 3 компьютера из имеющихся 3 типов:
Сколько существует монотонных слов длины 6 в алфавите из 2 символов:
Количество монотонных слов длины  в алфавите из
в алфавите из  символов:
символов:
Сколько существует способов инвестировать 3 миллиона рублей в какие-то из 3 проектов так, чтобы проекты получали целое число миллионов и все деньги были инвестированы:
Сколько существует способов представить целое число 4 в виде суммы целых неотрицательных слагаемых:
Укажите числа сочетаний, равные единице:
Чему равно  :
:
Определите производящую функцию для последовательности 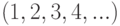
В формуле свертки 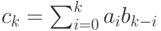 значение коэффициента
значение коэффициента 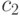 равно:
равно:
Бином Ньютона - это бином вида:
Выражение ![\sum_{k=0}^{[\frac{n}{2}]} (-1)^k \binom{n}{2k+1}](https://intuit.ru//sites/default/files/tex_cache/a1004df00886bf6a579e09899fd0eb1c.png) равно:
равно:
Чему равна сумма коэффициентов при четных степенях  бинома
бинома  :
:
Чему равна сумма квадратов коэффициентов при степенях бинома 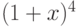 :
:
Укажите эквивалентные записи для полиномиальных коэффициентов 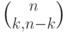 через числа сочетаний:
через числа сочетаний:
Чему равно количество размещений 5 различных объектов по 3 различным ящикам при условии, что в первом ящике находится 1 объект, во втором - 2 объекта, в третьем - 2 объекта:
Чему равна сумма полиномиальных коэффициентов разложения по степеням выражения 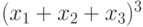 :
:
Сколько существует различных разбиений множества из 4 элементов на 2 класса:
Сколько существует разбиений  объектов на
объектов на  классов, таких что объект с номером
классов, таких что объект с номером  - единственный в своем классе:
- единственный в своем классе:
Сколько существует разбиений  объектов на
объектов на  классов, таких что объект с номером
классов, таких что объект с номером  не является единственным в своем классе:
не является единственным в своем классе:
Сколько существует сюръективных отображений из множества, состоящего из  элементов на множество из
элементов на множество из  элементов:
элементов:
Укажите верный способ выразить степень переменной через нижние степени переменной:
Сколько существует всевозможных отображений множества, состоящего из  элементов, в множество, состоящее из
элементов, в множество, состоящее из  элементов:
элементов:
Числа Белла выражаются через числа Стирлинга так:
Основная польза метода включений-исключений состоит в следущем:
Решение задачи о подсчете количества элементов в объединении трех множеств  с применением метода включений-исключений имеет вид:
с применением метода включений-исключений имеет вид:
Как в комбинаторике называют задачу, шутливая формулировка которой такова: "В лондонском клубе швейцар выдает шляпы наобум. Какова вероятность того, что ни один посетитель не получит свою шляпу?"
Приближенное значение выражения 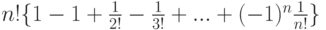 равно:
равно:
Укажите верное рекуррентное соотношение для числа беспорядков:
Укажите точное значение числа беспорядков на множестве из  элементов:
элементов:
Формула явного вида для чисел Стирлинга II рода может быть записана как:
Количество разбиений 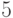 объектов на
объектов на  непустых класса равно
непустых класса равно 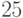 . Вычислите количество сюръективных отображений из множества, содержащего
. Вычислите количество сюръективных отображений из множества, содержащего 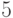 элементов, на множество, содержащее
элементов, на множество, содержащее  элемента:
элемента:
Система различных представителей:
Что из перечисленного ниже есть система различных представителей для системы подмножеств 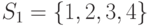 ,
, 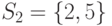 ,
, 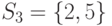 ,
, 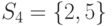 исходного множества
исходного множества 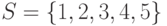
Система различных представителей для совокупности из  множеств
множеств 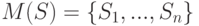 существует тогда и только тогда, когда:
существует тогда и только тогда, когда:
Замена представителей - это:
Система общих представителей - это:
Укажите возможные ситуации для системы общих представителей  при разбиениях множества
при разбиениях множества 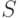
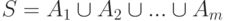 и
и 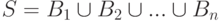 , для
, для 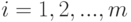 ,
, 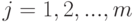 :
:
Укажите название известной головоломки: "Можно ли произвольную географическую карту раскрасить в 4 цвета так, чтобы ни одни 2 государства, граница которых имеется и отлична от точки, не были окрашены в один и тот же цвет".
Для графов с каким количеством вершин удобно их графическое представление в виде точек и соединяющих их линий:
Как формально определяется граф:
Укажите, где понятие "инцидентность" использовано верно:
Укажите выражения, описывающие количество ребер в полном неориентированном графе с количеством вершин  :
:
Вершине неориентированного графа инцидентны три ребра, петель и кратных ребер в графе нет. Определите степень вершины:
В неориентированном графе количество вершин нечетной степени:
Отметьте среди последовательностей степеней вершин такие, которым соответствует реально существующий граф:
Укажите способы машинного представления графа:
Укажите достоинства списков инциденций как способа машинного представления графа:
Длина пути в графе - это:
Какова минимальная длина цикла в простом графе:
Как соотносятся между собой графы  и
и  , если множество вершин графа
, если множество вершин графа  является подмножеством вершин графа
является подмножеством вершин графа  и все ребра графа
и все ребра графа  яаляются ребрами графа
яаляются ребрами графа  :
:
Представление графа в виде объединения связанных компонент - это:
Укажите последовательность степеней вершин существующего графа, которая требует связности первой и второй вершины:
Максимальное количество ребер в простом графе с 4 вершинами и 2 компонентами связности равно:
Укажите нижнюю границу количества ребер простого графа с  вершинами, превышение которой означает связность графа:
вершинами, превышение которой означает связность графа:
Укажите максимальное количество ребер, которое может содержаться в простом несвязном графе с 5 вершинами:
Какой неориентированный граф по определению называется деревом:
Вершина дерева называется концевой вершиной, если:
Количество деревьев, которое можно построить на 10 заданный вершинах, равно:
Какие из методов доказательства применяются при подсчете количества деревьев на  вершинах с
вершинах с  концевыми вершинами:
концевыми вершинами:
Сколько существует деревьев на 6 вершинах с 4 концевыми вершинами:
Формулировка задачи о кенигсбергских мостах в терминах теории графов выглядит так:
В каких задачах встречаются эйлеровы пути
В конечном неориентированном графе эйлеров путь существует тогда и только тогда, когда:
Конечный неориентрованный граф имеет эйлеров цикл тогда и тольо тогда, когда:
Путь имеет тип цикла, если:
Некоторый простой путь называется полным, если:
Каким свойством обладает длина максимальных путей в графе без гамильтоновых циклов:
Укажите достаточное условие существования гамильтонова пути в графе с  вершинами:
вершинами:
Степенной последовательностью графа называют:
Для какого графа наименьшее количество вершин, удаление которых приводит к несвязному или одновершинному графу, равно двум:
Для какого графа наименьшее количество вершин, удаление которых приводит к несвязному или одновершинному графу, равно трем:
Любой четырехсвязный планарный граф:
Расстояние от одной вершины графа до другой - это:
Чему равно количество размещений n различных объектов по  различным ящикам при условии, что в каждом ящике находится
различным ящикам при условии, что в каждом ящике находится 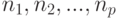 объектов соответственно,
объектов соответственно, 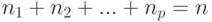 :
:
Количество деревьев, которое можно построить на 3 заданный вершинах, равно:
Многочлен Жегалкина для функции  имеет вид:
имеет вид:
Сколько сюръективных отображений соответствует каждому разбиению множества  из
из  элементов на
элементов на  классов:
классов:
Укажите максимальное количество ребер, которое может содержаться в простом несвязном графе с 3 вершинами:
В каких случаях имеет место указанная равносильность формул:
Укажите выражения, равные количеству размещений  одинаковых объектов по
одинаковых объектов по  различным ящикам:
различным ящикам:
Укажите самый неудобный способ машинного представления графа:
Основная лемма критерия полноты обосновывает возможность, при определенных условиях, получения функций:
Укажите функцию, представление которой в виде полинома Жегалкина содержит конъюнкцию с двумя или более переменными:
Сколько существует перестановок элементов множества  , состоящего из
, состоящего из  элементов, таких, что ровно
элементов, таких, что ровно  ,
,  , элементов стоят на своих местах, а остальные
, элементов стоят на своих местах, а остальные 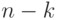 элементов расположены случайно:
элементов расположены случайно:
Разложение функции алгебры логики в дизъюнктивную форму по одной переменной:
Какие из перечисленных функций является монотонными?
Укажите необходимые свойства системы функций, из которых можно получить набор функций  :
:
Какие равенства представляют собой правила поглощения:
Что является разложением функции алгебры логики  в дизъюнктивную форму по переменной
в дизъюнктивную форму по переменной 
К основным задачам комбинаторики относятся:
Количество деревьев, которое можно построить на 4 заданных вершинах, равно:
Чему равна сумма всех чисел сочетаний из  по
по  :
:
Чему равна сумма квадратов коэффициентов при степенях бинома 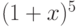 :
:
Цикл, по определению, - это:
Путь назвается простым, если:
Укажите количество сюръективных отображений 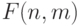 из множества
из множества 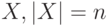 , на множество
, на множество 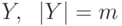 :
:
В каких случаях формулы  и
и  равносильны:
равносильны:
Какова максимальная длина простого пути в графе с  вершинами:
вершинами:
Имеется 4 конверта и 5 марок. Сколько существует способов выбрать конверт и марку для одного письма:
Укажите полные системы функций:
Продолжите утверждение: "В связном графе либо имеется гамильтонов цикл, либо:
Процедура перенумерации вершин графа так, чтобы номер вершины, куда ведет ребро, был больше, чем номер вершины-предшественника, называется:
Сколько существует способов представить целое число 3 в виде суммы целых неотрицательных слагаемых:
Что является разложением функции алгебры логики  в дизъюнктивную форму по переменной
в дизъюнктивную форму по переменной 
Производящая функция - это:
Функция алгебры логики - это:
Какие из перечисленных утверждений верны:
Что из перечисленного ниже вводится как функция алгебры логики:
Как связаны между собой элементарные функции алгебры логики:
В каких случаях имеет место указанная равносильность формул:
Совершенная конъюнктивная нормальная форма функции алгебры логики:
Совершенная конъюнктивная нормальная форма функции алгебры логики:
Примерами полных систем функции алгебры логики являются:
Получить функцию алгебры логики от двух переменных, применяя операции суперпозиции и замены переменной над классом функций алгебры логики одной переменной:
Количество функций от  переменных в классе функций, сохраняющих ноль, равно:
переменных в классе функций, сохраняющих ноль, равно:
К классу функций алгебры логики, сохраняющих единицу, относятся:
Какая из перечисленных функций является монотонной:
Функция алгебры логики, зависящая от  переменных, представима в виде полинома Жегалкина:
переменных, представима в виде полинома Жегалкина:
Сколько существует различных многочленов Жегалкина от  переменных:
переменных:
Укажите полные системы функций:
Укажите необходимое свойство системы функций, из которых можно получить набор функций  :
:
С помощью каких операций можно получить константу из любой несамодвойственной функции алгебры логики:
Для того, чтобы система функций  была полна, необходимо и достаточно, чтобы:
была полна, необходимо и достаточно, чтобы:
К модельным задачам комбинаторики относятся:
Укажите количество всевозможных размещений  различных объектов по
различных объектов по  различным ящикам:
различным ящикам:
Укажите количество различных слов длиной в 3 символа, в которых все символы различны, в алфавите из 5 символов:
Укажите выражения, равные количеству всевозможных размещений  различных объектов по
различных объектов по  различным ящикам при условии, что в каждом ящике не более 1 объекта:
различным ящикам при условии, что в каждом ящике не более 1 объекта:
Чему равно число Стирлинга первого рода 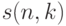 при
при  :
:
Чему равно число Стирлинга первого рода 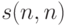 :
:
Сколько существует различных способов расставить 2 разные книги по 10 книжным полкам:
Сколько существует способов закупить 4 компьютера из имеющихся 3 типов:
Монотонное слово длины  - это:
- это:
Для целых положительных чисел  и
и  выражение
выражение ![[m]^n](https://intuit.ru//sites/default/files/tex_cache/b4c508e89ac816704bfcd76461528bbf.png) делится нацело на
делится нацело на 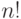 :
:
Укажите числа сочетаний, равные нулю:
Выражение 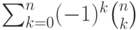 равно:
равно:
Чему равно число сочетаний 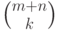 :
:
Какая функция является производящей для полиномиальных коэффициентов 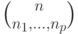 :
:
Чему равна сумма полиномиальных коэффициентов разложения по степеням выражения 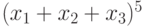 :
:
Сколько существует различных разбиений множества из 4 элементов на 3 класса:
Укажите верные равенства о количестве разбиений множества из  элементов на
элементов на  классов:
классов:
Сколько существует сюръективных отображений из множества, состоящего из 4 элементов на множество из 2 элементов:
Укажите верное рекуррентное соотношение для чисел Стирлинга II рода:
Основная задача метода включений-исключений - это:
Задача о подсчете количества элементов  в объединении трех множеств
в объединении трех множеств  решается методом включений-исключений. Укажите возможные списки свойств объектов:
решается методом включений-исключений. Укажите возможные списки свойств объектов:
В комбинаторике беспорядком называют:
Приближенное значение доли беспорядков ко всем перестановкам конечного множества  , состоящего из
, состоящего из  элементов, равно:
элементов, равно:
Сколько существует беспорядков для множества, состоящего из  элемента, таких, что элемент
элемента, таких, что элемент  стоит на
стоит на  -ом месте, а элемент
-ом месте, а элемент  НЕ стоит на
НЕ стоит на  -ом месте:
-ом месте:
Система различных представителей:
В каких случаях нельзя построить систему различных представителей для  множеств:
множеств:
Укажите условие существования системы общих представителей для разбиений 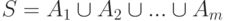 и
и 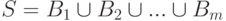 :
:
Как можно доказать существование системы общих представителей в общем случае:
Формула включений-исключений имеет вид:
Какие из формул равносильны формуле  :
:
Укажите обозначения для числа сочетаний из  элементов по
элементов по  элементов:
элементов:
Сколько ребер содержит дерево с  вершинами?
вершинами?
Укажите верные утверждения:
Какой способ наиболее эффективен при подсчете количества деревьев:
Некоторая функция алгебры логики зависит от 64 аргументов. Количество элементов в множестве значений данной функции алгебры логики равно:
По определению, эйлеров путь для конечного неориентированного графа -это:
Укажите комбинаторный смысл полиномиальных коэффициентов 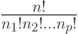 , где
, где 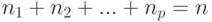 , в терминах слов в алфавите:
, в терминах слов в алфавите:
Функция алгебры логики задана на двух аргументах. Количество элементов в множестве значений данной функции алгебры логики равно:
В каких случаях имеет место указанная равносильность формул:
Совершенная дизъюнктивная нормальная форма функции алгебры логики:
Образ ямы, из которой нельзя вылезти с помощью операции суперпозиции и замены переменных, на поле всех функций алгебры логики от n переменных иллюстрирует понятие:
Какое значение принимает самодвойственная функция на наборе  , если на наборе
, если на наборе  эта функция принимает значение
эта функция принимает значение  ?
?
Количество монотонных функций алгебры логики от n переменных:
Укажите, какие функции алгебры логики могут быть представлены в виде полинома Жегалкина:
Укажите полную систему функций:
Многочлен Жегалкина для функции 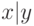 имеет вид:
имеет вид:
Укажите необходимое свойство системы функций, из которых можно получить набор функций  :
:
Укажите количество способов поставить четырем студентам оценки "удовлетворительно", "хорошо", "отлично":
Укажите выражения, равные количеству различных слов длины  , в которых все символы различны, в алфавите из
, в которых все символы различны, в алфавите из  символов:
символов:
Укажите количество способов разместить 4 шарика по 4 лункам при условии, что в каждой лунке не более 1 шарика:
Чему равно число Стирлинга первого рода 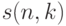 при
при  :
:
В записи числа Стирлинга первого рода 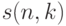 индекс
индекс  означает, что:
означает, что:
Для двух способов упорядоченного размещения  различных объектов по
различных объектов по  различным ящикам верно следующее:
различным ящикам верно следующее:
Сколько существует монотонных слов длины 4 в алфавите из 3 символов:
Количество монотонных слов длины  в алфавите из
в алфавите из  символов равно:
символов равно:
Укажите выражения, равные числу сочетаний из  элементов по
элементов по  элементов:
элементов:
Выражение ![\sum_{k=0}^{[\frac{n}{2}]} (-1)^k \binom{n}{2k}](https://intuit.ru//sites/default/files/tex_cache/772c6794adbb059db01176122b11fed8.png) равно:
равно:
Выпишите числа сочетаний для 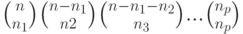 в факториальной форме::
в факториальной форме::
Сколько существует способов разместить  различных объектов по
различных объектов по  различным ящикам, при условии, что в каждом ящике находится
различным ящикам, при условии, что в каждом ящике находится 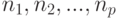 объектов соответственно,
объектов соответственно, 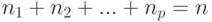 , и один из размещаемых объектов уже лежит в ящике
, и один из размещаемых объектов уже лежит в ящике  :
:
Чему равна сумма полиномиальных коэффициентов разложения по степеням выражения 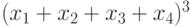 :
:
Числами Стирлинга II рода называют:
Укажите верное рекуррентное соотношение для числа разбиений:
Сколько существует разбиений из 4 элементов на 2 класса:
Для любого сюръективного отображения верно, что:
Довод, согласно которому из равенства нулю полинома конечной степени в бесконечном множестве целых значений переменной следует равенство полинома нулю для всех вещественных чисел, называют в комбинаторике:
Выразите задачу размещения  одинаковых объектов по
одинаковых объектов по  различным ящикам в терминах задачи Муавра:
различным ящикам в терминах задачи Муавра:
Укажите верное рекуррентное соотношение для числа беспорядков:
Количество разбиений  объектов на
объектов на 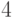 непустых класса равно
непустых класса равно  . Вычислите количество сюръективных отображений из множества, содержащего
. Вычислите количество сюръективных отображений из множества, содержащего  элементов, на множество, содержащее
элементов, на множество, содержащее 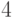 элемента:
элемента:
Что из перечисленного ниже есть система различных представителей для системы подмножеств 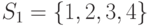 ,
, 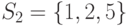 ,
, 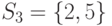 ,
, 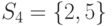 исходного множества
исходного множества 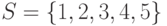 :
:
Укажите приложения теории графов:
Какая задача в терминах теории графов решалась в связи с проблемой неплатежей после начала перестройки, при наличии списка должников:
Укажите, где понятие "смежность" использовано верно:
Отметьте среди последовательностей степеней вершин такие, которым соответствует реально существующий граф:
Способ представления графа в виде матрицы, в которой строки соответствуют вершинам графа, а столбцы - ребрам, называется:
Способ представления графа в виде матрицы, в которой столбцы и строки соответствуют вершинам графа, называется:
Единственные вершины нечетной степени в простом графе:
Максимальное количество ребер в простом графе с 3 вершинами и 2 компонентами связности равно:
Укажите максимальное количество ребер, которое может содержаться в простом несвязном графе с 4 вершинами:
Количество деревьев, которое можно построить на 2 заданный вершинах, равно:
Сколько существует деревьев на 3 вершинах с 2 концевыми вершинами:
Началом и концом эйлерова пути могут быть вершины:
Как соотносятся между собой эйлеровы пути и эйлеровы циклы в графе:
Гамильтонов путь на простом неориентрованном графе - это:
Если степень каждой из вершин графа строго больше половины количества вершин графа, то:
Граф называется гамильтоновым, если он:
Двухсвязный негамильтонов граф:
Длина пути в ориентированном графе с весами ребер - это:
Укажите количество различных слов длиной в 3 символа в алфавите из 5 символов:
Максимальный полный путь в связном графе имеет тип цикла тогда и только тогда, когда:
Сколько ребер содержит дерево со 100 вершинами?
Множество деревьев на  вершинах с
вершинах с  концевыми вершинами имеет взаимнооднозначное соответствие с этим множеством:
концевыми вершинами имеет взаимнооднозначное соответствие с этим множеством:
Эйлеров путь может существовать в графе, количество вершин нечетной степени в котором:
Неориентированный граф называют простым графом, если этот граф:
Что соответствует вершинам и ребрам графа, который описывает "Задачу о четырех красках":
Многочлен Жегалкина для функции 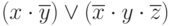 имеет вид:
имеет вид:
Сколько существует способов инвестировать 4 миллиона рублей в какие-то из 3 проектов так, чтобы проекты получали целое число миллионов и все деньги были инвестированы:
Укажите множество, с которым у множества деревьев с  вершинами имеется взаимнооднозначное соответствие:
вершинами имеется взаимнооднозначное соответствие:
Две формулы называются равносильными, если они:
Что является разложением функции алгебры логики  в дизъюнктивную форму по переменной
в дизъюнктивную форму по переменной 
Если операциями суперпозиции и замены переменных из функций данной системы функций алгебры логики можно получить только функции, ей принадлежащие, и никаких других функций, то такая система функций:
Количество функций алгебры логики от n переменных, сохранящих единицу, равно:
Функцией, двойственной к  , является:
, является:
Объект  может быть выбран
может быть выбран  различными способами, объект
различными способами, объект  может быть выбран
может быть выбран  различными способами, одновременный выбор объектов
различными способами, одновременный выбор объектов  и
и  невозможен. Тогда:
невозможен. Тогда:
Для двух чисел Стирлинга 1 рода, не равных нулю, 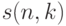 и
и  :
:
Укажите выражения, равные количеству инъективный отображений из множества  в множество
в множество  , где
, где  - конечное множество из
- конечное множество из  элементов,
элементов,  - конечное множество из
- конечное множество из  элементов:
элементов:
Сколько существует способов инвестировать 5 миллионов рублей в какие-то из 3 проектов так, чтобы проекты получали по целому число миллионов и все деньги были инвестированы:
Сверткой в комбинаторике называют:
Что является производящей функцией последовательности 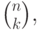
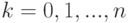 :
:
Сколько существует разбиений из 5 элементов на 2 класса:
Что соответствует понятию сюръективного отображения в терминах размещения объектов по ящикам:
В комбинаторике перестановкой элементов конечного множества  называют:
называют:
Если система различных представителей для совокупности из  множеств существует, то:
множеств существует, то:
Для совокупности из  множеств
множеств 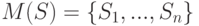 для каждого
для каждого 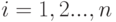 последовательно выбрали
последовательно выбрали 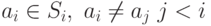 . Тогда выбранный набор
. Тогда выбранный набор 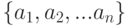 :
:
Укажите выражение, описывающие количество ребер в полном ориентированном графе с количеством вершин  :
:
Отметьте среди последовательностей степеней вершин такие, которым соответствует реально существующий граф:
При котором из способов представления графа матрица для его представления всегда квадратная:
Как соотносятся между собой графы  и
и  , если множество вершин графа
, если множество вершин графа  является подмножеством вершин графа
является подмножеством вершин графа  и множество ребер графа
и множество ребер графа  состоит из всех ребер графа
состоит из всех ребер графа  , соединяющих вершины графа
, соединяющих вершины графа  :
:
По определению, граф называется связным, если:
Что из перечисленного есть термины теории графов:
Любое нетривиальное дерево содержит::
Количество слов длины  в алфавите из
в алфавите из 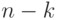 символов, причем каждый символ входит в это слово, равно:
символов, причем каждый символ входит в это слово, равно:
Чем замечательны эйлеровы пути и эйлеровы циклы на практике:
Полным максимальным путем называют:
В каких задачах применяются ориентированные графы с весами ребер:
К задачам комбинаторики относятся:
Сколько существует монотонных слов длины 7 в алфавите из 2 символов:
Какие из перечисленных функций являются самодвойственными:
Определите сложность решения задачи поиска кратчайших путей в орграфе без циклов отрицательной длины,  - количество вершин графа
- количество вершин графа
Чему равна сумма квадратов чисел сочетаний 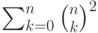 :
:
К классу функций алгебры логики, сохраняющих ноль, относятся:
С помощью каких операций над функциями можно получить из самодвойственной функции константу:
Укажите необходимое свойство системы функций, из которых можно получить набор функций  :
:
Укажите количество способов поставить трем студентам оценки "удовлетворительно", "хорошо", "отлично", чтобы все студенты получили разные оценки::
Число различных упорядоченных размещений  различных объектов по
различных объектов по  различным ящикам равно:
различным ящикам равно:
Определите производящую функцию для последовательности 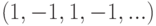
Чему равно количество размещений 6 различных объектов по 3 различным ящикам при условии, что в первом ящике находится 1 объект, во втором - 2 объекта, в третьем - 3 объекта:
Рекуррентное соотношение для чисел Белла имеет вид:
Запишите формулу включений-исключений для трех свойств:
Укажите точное значение числа беспорядков на множестве из  элементов:
элементов:
Как формально определяется множество ребер ориентированного графа:
Укажите вершины графа, степень которых равна нулю:
Для доказательства изоморфности двух графов:
В формулировке задачи о кенигсбергских мостах в терминах теории графов:
Укажите верные утверждения:
Укажите достаточное условие существования гамильтонова цикла в графе с  вершинами:
вершинами:
В каких случаях имеет место указанная равносильность формул:
Укажите количество всевозможных отображений из множества  в множество
в множество  , где
, где  - конечное множество из
- конечное множество из  элементов,
элементов,  - конечное множество из
- конечное множество из  элементов:
элементов:
Укажите количество способов разместить 4 шарика по 5 лункам при условии, что в каждой лунке не более 1 шарика:
Для системы общих представителей  при разбиениях множества
при разбиениях множества 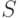
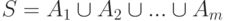 и
и 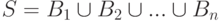 справедливо, для
справедливо, для 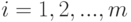 :
:
Какие из функций алгебры логики принимают значение при значениях аргументов 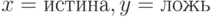
Функцией, двойственной к 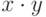 , является:
, является:
К каким классам функций алгебры логики относится функция  :
:
Сколько существует упорядоченных размещений 2 объектов по 2 ящикам:
Сколько существует способов инвестировать 3 миллиона рублей в какие-то из 10 проектов так, чтобы проекты получали целое число миллионов и все деньги были инвестированы:
Базис в пространстве многочленов образуют:
Сколько существует беспорядков для множества, состоящего из  элемента, таких, что элемент
элемента, таких, что элемент  стоит на
стоит на  -ом месте, а элемент
-ом месте, а элемент  - на
- на  -ом месте:
-ом месте:
При построении системы различных представителей:
При построении С.Р.П. для совокупности из  множеств
множеств 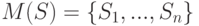 для первых
для первых  множеств,
множеств, 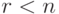 , удалось выбрать различных представителей, но все элементы множества
, удалось выбрать различных представителей, но все элементы множества 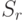 уже использованы в качестве представителей предыдущих множеств. Тогда:
уже использованы в качестве представителей предыдущих множеств. Тогда:
Появление теории графов как математической дисциплины связывают с датой этого события:
Укажите соотношение между количество ребер в полном ориентированном графе и количеством ребер в полном неориентированном графе, оба графа с количеством вершин  :
:
Отметьте среди последовательностей степеней вершин такие, которым соответствует реально существующий граф:
Укажите верные утверждения:
По определению, две вершины называются связанными, если:
Максимальное количество ребер в простом графе с 5 вершинами и 2 компонентами связности равно:
Простой граф, имещий две вершины степени 3, соединенные тремя непересекающимися путями длины не менее 2, называется:
Оцените сложность алгоритма построения эйлерова цикла в графе с количеством вершин  и количеством ребер
и количеством ребер  :
:
Какие из функций алгебры логики принимают значение при значениях аргументов 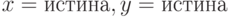
Укажите системы функций, не являщихся полными:
Укажите выражения, равные количеству различных слов длины  , в которых все символы различны, в алфавите из
, в которых все символы различны, в алфавите из  символов:
символов:
Конечный граф - это граф, у которого:
Граф называется негамильтоновым, если он:
Определите сложность решения задачи поиска кратчайших путей в графе без циклов,  - количество вершин графа:
- количество вершин графа:
Cовершенная конъюнктивная нормальная форма для импликации  имеет вид:
имеет вид:
Сколько существует различных способов расставить 10 разных книг по 2 книжным полкам:
Чему равна сумма коэффициентов при нечетных степенях  бинома
бинома 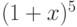 :
:
Укажите взимосвязь чисел Стирлинга II рода 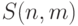 и количества сюръективных отображений
и количества сюръективных отображений 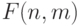 :
:
Понятие системы общих представителей формулируется для:
Укажите верные утверждения:
Укажите свойство простого графа с количеством вершин  и количеством ребер большим
и количеством ребер большим 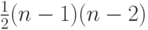 :
:
Чему равно 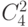 :
:
К каким классам функций алгебры логики относится функция  :
:
Разбиение в терминах размещения объектов по ящикам - это:
Сколько существует деревьев на 4 вершинах с 2 концевыми вершинами:

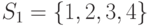 ,
, 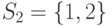 ,
,  ,
,  исходного множества
исходного множества 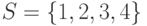
 - количество вершин графа:
- количество вершин графа: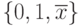 :
: , если на наборе
, если на наборе 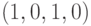 эта функция принимает значение
эта функция принимает значение  :
: может быть выбран
может быть выбран  различными способами, после этого объект
различными способами, после этого объект  может быть выбран
может быть выбран  различными способами. Тогда:
различными способами. Тогда: различных объектов по
различных объектов по  различным ящикам при условии, что в каждом ящике не более 1 объекта:
различным ящикам при условии, что в каждом ящике не более 1 объекта: на себя, где
на себя, где  - конечное множество из
- конечное множество из  элементов:
элементов: объектов на
объектов на  классов, таких что объект с номером
классов, таких что объект с номером  - единственный в своем классе:
- единственный в своем классе:  объектов на
объектов на  классов, таких что объект с номером
классов, таких что объект с номером  не является единственным в своем классе:
не является единственным в своем классе: элементов на множество из
элементов на множество из  элементов:
элементов: элементов, в множество, состоящее из
элементов, в множество, состоящее из  элементов:
элементов: с применением метода включений-исключений имеет вид:
с применением метода включений-исключений имеет вид: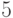 объектов на
объектов на  непустых класса равно
непустых класса равно 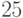 . Вычислите количество сюръективных отображений из множества, содержащего
. Вычислите количество сюръективных отображений из множества, содержащего 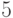 элементов, на множество, содержащее
элементов, на множество, содержащее  элемента:
элемента: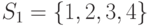 ,
, 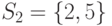 ,
, 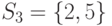 ,
, 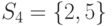 исходного множества
исходного множества 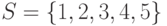
 множеств
множеств 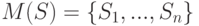 существует тогда и только тогда, когда:
существует тогда и только тогда, когда: :
: и
и  , если множество вершин графа
, если множество вершин графа  является подмножеством вершин графа
является подмножеством вершин графа  и все ребра графа
и все ребра графа  яаляются ребрами графа
яаляются ребрами графа  :
: вершинами, превышение которой означает связность графа:
вершинами, превышение которой означает связность графа: вершинах с
вершинах с  концевыми вершинами:
концевыми вершинами: различным ящикам при условии, что в каждом ящике находится
различным ящикам при условии, что в каждом ящике находится 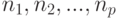 объектов соответственно,
объектов соответственно, 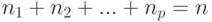 :
: , состоящего из
, состоящего из  элементов, таких, что ровно
элементов, таких, что ровно  ,
,  , элементов стоят на своих местах, а остальные
, элементов стоят на своих местах, а остальные 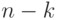 элементов расположены случайно:
элементов расположены случайно: различных объектов по
различных объектов по  различным ящикам при условии, что в каждом ящике не более 1 объекта:
различным ящикам при условии, что в каждом ящике не более 1 объекта: в объединении трех множеств
в объединении трех множеств  решается методом включений-исключений. Укажите возможные списки свойств объектов:
решается методом включений-исключений. Укажите возможные списки свойств объектов: , состоящего из
, состоящего из  элементов, равно:
элементов, равно: элемента, таких, что элемент
элемента, таких, что элемент  стоит на
стоит на  -ом месте, а элемент
-ом месте, а элемент  НЕ стоит на
НЕ стоит на  -ом месте:
-ом месте: , если на наборе
, если на наборе  эта функция принимает значение
эта функция принимает значение  ?
? , в которых все символы различны, в алфавите из
, в которых все символы различны, в алфавите из  символов:
символов: различных объектов по
различных объектов по  различным ящикам, при условии, что в каждом ящике находится
различным ящикам, при условии, что в каждом ящике находится 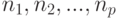 объектов соответственно,
объектов соответственно, 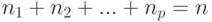 , и один из размещаемых объектов уже лежит в ящике
, и один из размещаемых объектов уже лежит в ящике  :
: объектов на
объектов на 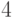 непустых класса равно
непустых класса равно  . Вычислите количество сюръективных отображений из множества, содержащего
. Вычислите количество сюръективных отображений из множества, содержащего  элементов, на множество, содержащее
элементов, на множество, содержащее 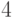 элемента:
элемента: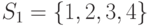 ,
, 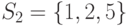 ,
, 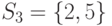 ,
, 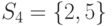 исходного множества
исходного множества 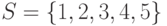 :
: вершинах с
вершинах с  концевыми вершинами имеет взаимнооднозначное соответствие с этим множеством:
концевыми вершинами имеет взаимнооднозначное соответствие с этим множеством: вершинами имеется взаимнооднозначное соответствие:
вершинами имеется взаимнооднозначное соответствие: может быть выбран
может быть выбран  различными способами, объект
различными способами, объект  может быть выбран
может быть выбран  различными способами, одновременный выбор объектов
различными способами, одновременный выбор объектов  и
и  невозможен. Тогда:
невозможен. Тогда: в множество
в множество  , где
, где  - конечное множество из
- конечное множество из  элементов,
элементов,  - конечное множество из
- конечное множество из  элементов:
элементов: :
: и
и  , если множество вершин графа
, если множество вершин графа  является подмножеством вершин графа
является подмножеством вершин графа  и множество ребер графа
и множество ребер графа  состоит из всех ребер графа
состоит из всех ребер графа  , соединяющих вершины графа
, соединяющих вершины графа  :
: - количество вершин графа
- количество вершин графа в множество
в множество  , где
, где  - конечное множество из
- конечное множество из  элементов,
элементов,  - конечное множество из
- конечное множество из  элементов:
элементов: элемента, таких, что элемент
элемента, таких, что элемент  стоит на
стоит на  -ом месте, а элемент
-ом месте, а элемент  - на
- на  -ом месте:
-ом месте: множеств
множеств 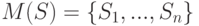 для первых
для первых  множеств,
множеств, 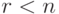 , удалось выбрать различных представителей, но все элементы множества
, удалось выбрать различных представителей, но все элементы множества 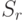 уже использованы в качестве представителей предыдущих множеств. Тогда:
уже использованы в качестве представителей предыдущих множеств. Тогда: :
: и количеством ребер
и количеством ребер  :
: , в которых все символы различны, в алфавите из
, в которых все символы различны, в алфавите из  символов:
символов: - количество вершин графа:
- количество вершин графа: